Een complete gids: het 2×2 factoriële ontwerp

Een 2 × 2 factorieel ontwerp is een soort experimenteel ontwerp waarmee onderzoekers de effecten van twee onafhankelijke variabelen (elk met twee niveaus ) op een enkele afhankelijke variabele kunnen begrijpen.

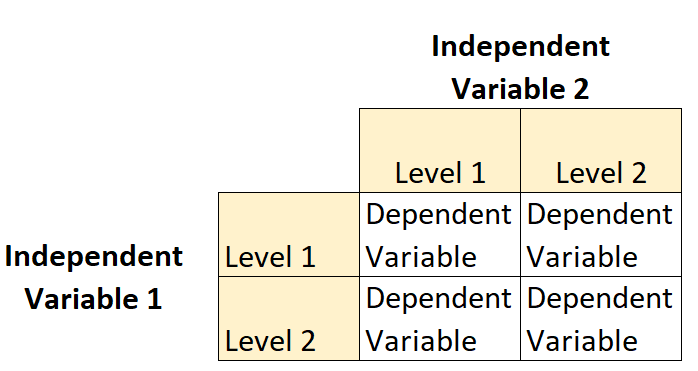
Stel bijvoorbeeld dat een botanicus inzicht wil krijgen in de effecten van zonlicht (laag of hoog) en de waterfrequentie (dagelijks of wekelijks) op de groei van een bepaalde plantensoort.

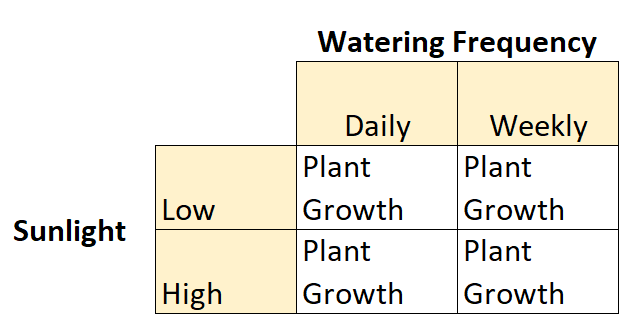
Dit is een voorbeeld van een 2×2 factorieel ontwerp omdat er twee onafhankelijke variabelen zijn, elk met twee niveaus:

• Onafhankelijke variabele #1: zonlicht
  • Niveaus: laag, hoog
• Onafhankelijke variabele #2: Besproeiingsfrequentie
  • Niveaus: dagelijks, wekelijks

En er is een afhankelijke variabele: plantengroei.

Het doel van een 2×2 factorieel ontwerp

Een 2×2 factorieel ontwerp maakt het mogelijk om de volgende effecten te analyseren:

Belangrijkste effecten: Dit zijn de effecten die een enkele onafhankelijke variabele heeft op de afhankelijke variabele.

In ons vorige scenario konden we bijvoorbeeld de volgende hoofdeffecten analyseren:

• Belangrijkste effect van zonlicht op de plantengroei.
  • We kunnen de gemiddelde groei vinden van alle planten die weinig zonlicht hebben gekregen.
  • We kunnen de gemiddelde groei vinden van alle planten die veel zonlicht hebben gekregen.
• Belangrijkste effect van de waterfrequentie op de plantengroei.
  • We kunnen de gemiddelde groei vinden van alle planten die dagelijks water krijgen.
  • We kunnen de gemiddelde groei vinden van alle planten die elke week water krijgen.

Interactie-effecten: Ze treden op wanneer het effect van één onafhankelijke variabele op de afhankelijke variabele afhangt van het niveau van de andere onafhankelijke variabele.

In ons vorige scenario konden we bijvoorbeeld de volgende interactie-effecten analyseren:

• Is het effect van zonlicht op de plantengroei afhankelijk van de waterfrequentie?
• Is het effect van de waterfrequentie op de plantengroei afhankelijk van zonlicht?

Visualiseer hoofdeffecten en interactie-effecten

Wanneer we een 2 × 2 factorieel ontwerp gebruiken, brengen we vaak de gemiddelden in kaart om de effecten die de onafhankelijke variabelen hebben op de afhankelijke variabele beter te begrijpen.

Beschouw bijvoorbeeld het volgende plot:

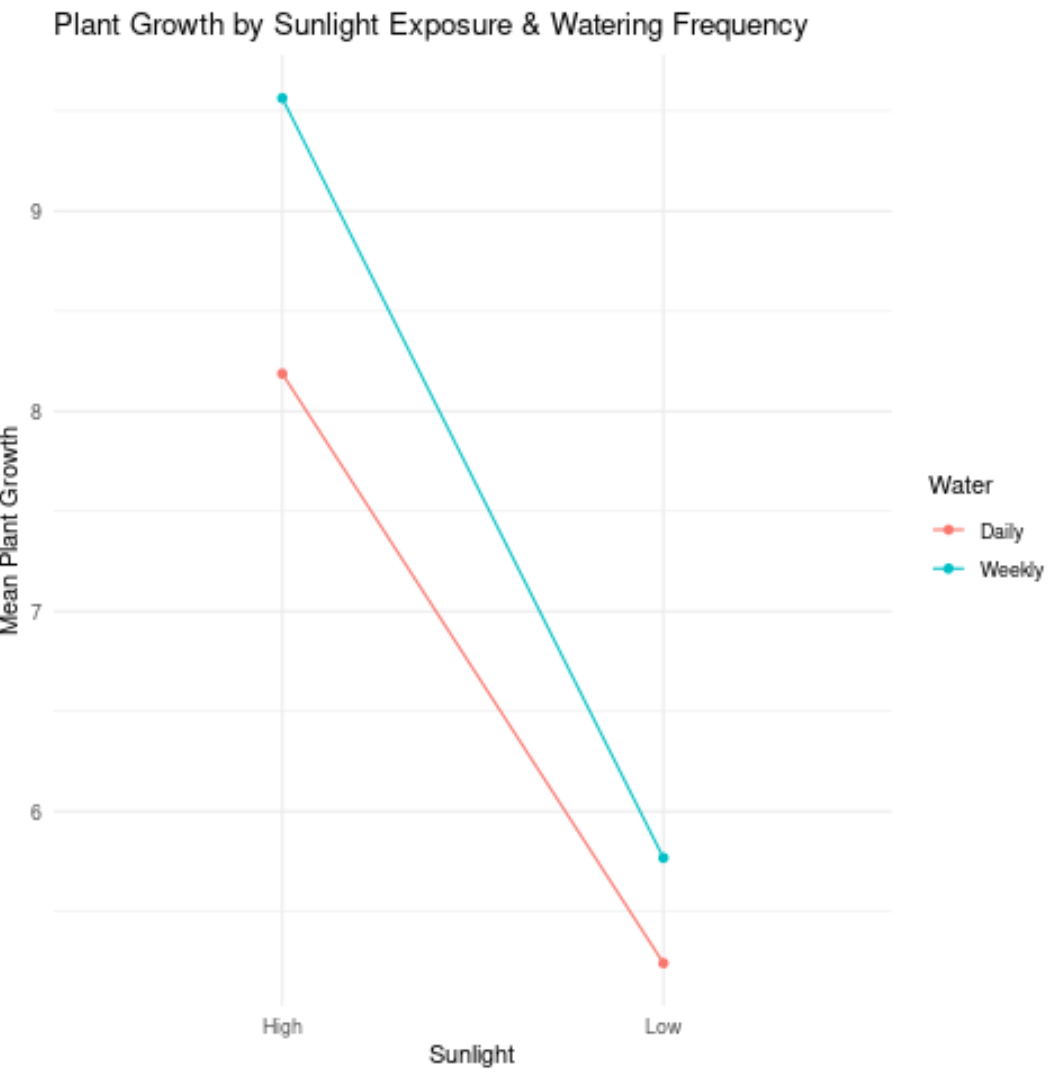
Zo interpreteert u de waarden in de plot:

• De gemiddelde groei van planten die intens zonlicht en dagelijkse watergift kregen, was ongeveer 23,5 cm.
• De gemiddelde groei van planten die veel zonlicht kregen en wekelijks water kregen, was ongeveer 9,6 inch.
• De gemiddelde groei van planten die weinig zon kregen en dagelijks water kregen, was ongeveer 17,5 cm.
• De gemiddelde groei van planten die weinig zon kregen en wekelijks water kregen, was ongeveer 17,5 cm.

Om te bepalen of er een interactie-effect is tussen de twee onafhankelijke variabelen, controleert u eenvoudig of de lijnen evenwijdig zijn of niet:

• Als de twee lijnen van de plot evenwijdig zijn, is er geen interactie-effect.
• Als de twee lijnen van de plot niet evenwijdig zijn, is er sprake van een interactie-effect.

In de vorige grafiek liepen de twee lijnen ongeveer evenwijdig, dus er is waarschijnlijk geen interactie-effect tussen de waterfrequentie en de blootstelling aan de zon.

Beschouw echter het volgende plot:

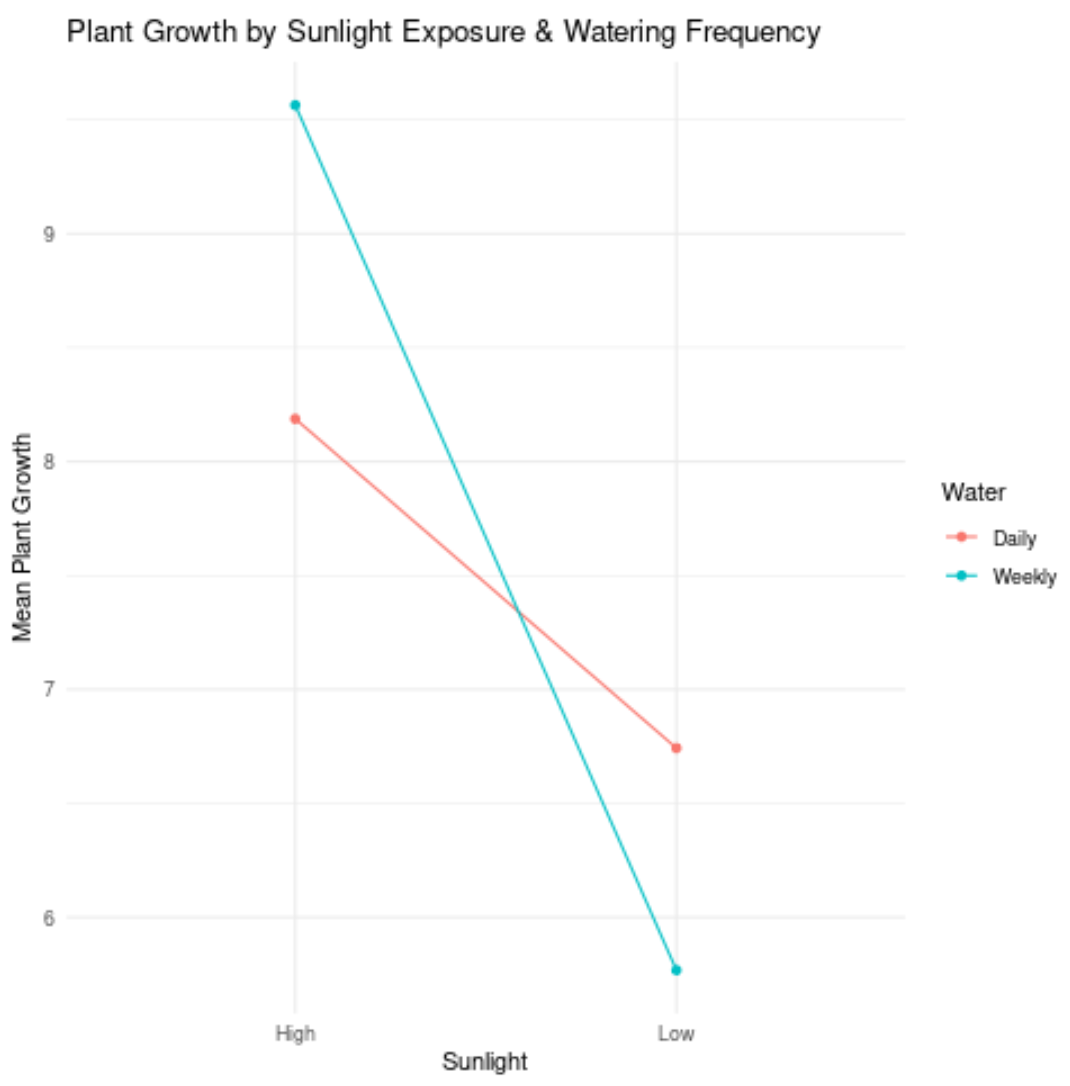
De twee lijnen zijn helemaal niet evenwijdig (ze snijden elkaar zelfs!), wat erop wijst dat er waarschijnlijk een interactie-effect tussen hen bestaat.

Dit betekent bijvoorbeeld dat het effect van zonlicht op de plantengroei afhankelijk is van de frequentie van water geven.

Met andere woorden: zonlicht en waterfrequentie hebben geen onafhankelijke invloed op de plantengroei. Er is eerder sprake van een interactie-effect tussen de twee onafhankelijke variabelen.

Hoe een 2×2 factorieel ontwerp te analyseren

Het plotten van gemiddelden is een visuele manier om de effecten te inspecteren die onafhankelijke variabelen hebben op de afhankelijke variabele.

We kunnen echter ook een tweerichtings-ANOVA uitvoeren om formeel te testen of de onafhankelijke variabelen al dan niet een statistisch significante relatie hebben met de afhankelijke variabele.

De volgende code laat bijvoorbeeld zien hoe u een tweerichtings-ANOVA uitvoert voor ons hypothetische fabrieksscenario in R:

 #make this example reproducible
set. seeds (0)

df <- data. frame (sunlight = rep(c(' Low ', ' High '), each = 30 ),
                 water = rep(c(' Daily ', ' Weekly '), each = 15 , times = 2 ),
                 growth = c(rnorm(15, 6, 2), rnorm(15, 7, 3), rnorm(15, 7, 2),
                                   rnorm(15, 10, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

               Df Sum Sq Mean Sq F value Pr(>F)   
sunlight 1 52.5 52.48 8.440 0.00525 **
water 1 31.6 31.59 5.081 0.02813 * 
sunlight:water 1 12.8 12.85 2.066 0.15620   
Residuals 56 348.2 6.22                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Zo interpreteert u het ANOVA-resultaat:

• De p-waarde geassocieerd met zonlicht is 0,005 . Omdat dit getal minder dan 0,05 bedraagt, betekent dit dat blootstelling aan zonlicht een statistisch significant effect heeft op de plantengroei.
• De p-waarde geassocieerd met water is 0,028 . Omdat dit cijfer minder dan 0,05 bedraagt, betekent dit dat de waterfrequentie ook een statistisch significant effect heeft op de plantengroei.
• De p-waarde voor de interactie tussen zonlicht en water is 0,156 . Omdat dit cijfer niet minder dan 0,05 bedraagt, betekent dit dat er geen interactie-effect is tussen zonlicht en water.

Aanvullende bronnen

Een complete gids: het 2 × 3 factoriële ontwerp
Wat zijn niveaus van een onafhankelijke variabele?
Onafhankelijke of afhankelijke variabelen
Wat is een factoriële ANOVA?