Een complete gids: het 2×3 factoriële ontwerp

Een 2 × 3 factorieel ontwerp is een soort experimenteel ontwerp waarmee onderzoekers de effecten van twee onafhankelijke variabelen op een enkele afhankelijke variabele kunnen begrijpen.

Bij dit type ontwerp heeft één onafhankelijke variabele twee niveaus en de andere onafhankelijke variabele drie niveaus.

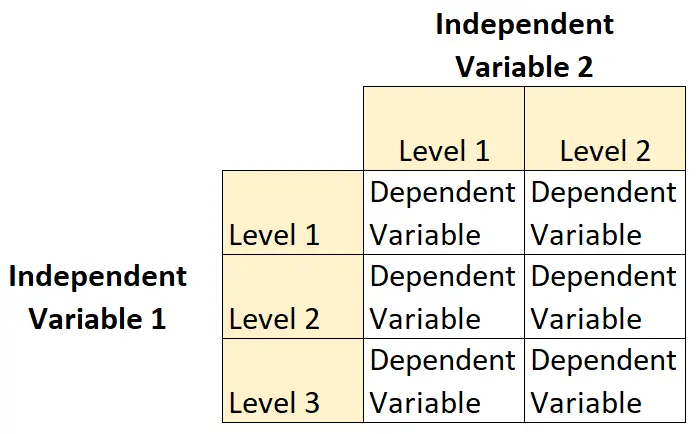
Stel bijvoorbeeld dat een botanicus inzicht wil krijgen in de effecten van zonlicht (laag, gemiddeld of hoog) en de waterfrequentie (dagelijks of wekelijks) op de groei van een bepaalde plantensoort.

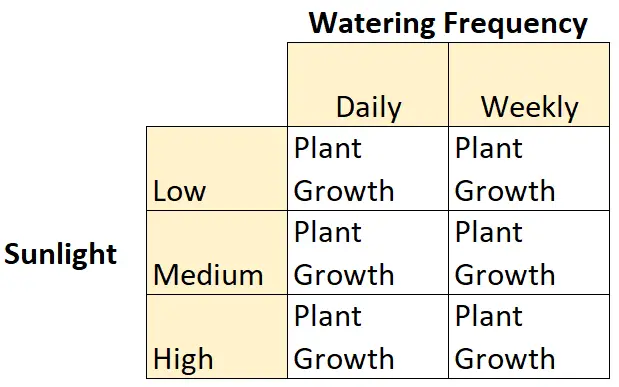
Dit is een voorbeeld van een 2 × 3 factorieel ontwerp omdat er twee onafhankelijke variabelen zijn, één met twee niveaus en één met drie niveaus:

• Onafhankelijke variabele #1: zonlicht
  • Niveaus: Laag, Gemiddeld, Hoog
• Onafhankelijke variabele #2: Besproeiingsfrequentie
  • Niveaus: dagelijks, wekelijks

En er is een afhankelijke variabele: plantengroei.

Het doel van een 2 × 3 factorieel ontwerp

Met een 2×3 factorieel ontwerp kunt u de volgende effecten analyseren:

Belangrijkste effecten: Dit zijn de effecten die een enkele onafhankelijke variabele heeft op de afhankelijke variabele.

In ons vorige scenario konden we bijvoorbeeld de volgende hoofdeffecten analyseren:

• Belangrijkste effect van zonlicht op de plantengroei.
  • Gemiddelde groei van alle planten die weinig zonlicht kregen.
  • Gemiddelde groei van alle planten die gemiddeld zonlicht kregen.
  • Gemiddelde groei van alle planten die veel zonlicht kregen.
• Belangrijkste effect van de waterfrequentie op de plantengroei.
  • Gemiddelde groei van alle planten die dagelijks water krijgen.
  • Gemiddelde groei van alle planten die elke week water krijgen.

Interactie-effecten: Ze treden op wanneer het effect van één onafhankelijke variabele op de afhankelijke variabele afhangt van het niveau van de andere onafhankelijke variabele.

In ons vorige scenario konden we bijvoorbeeld de volgende interactie-effecten analyseren:

• Is het effect van zonlicht op de plantengroei afhankelijk van de waterfrequentie?
• Is het effect van de waterfrequentie op de plantengroei afhankelijk van zonlicht?

Hoe een 2 × 3 factorieel ontwerp te analyseren

We kunnen een tweerichtings-ANOVA uitvoeren om formeel te testen of de onafhankelijke variabelen al dan niet een statistisch significante relatie hebben met de afhankelijke variabele.

De volgende code laat bijvoorbeeld zien hoe u een tweerichtings-ANOVA uitvoert voor ons hypothetische fabrieksscenario in R:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' Low ', ' Medium ', ' High '), each = 15, times = 2),
                 water = rep(c(' Daily ', ' Weekly '), each = 45, times = 2),
                 growth = c(rnorm(15, 9, 2), rnorm(15, 10, 3), rnorm(15, 13, 2),
                            rnorm(15, 8, 3), rnorm(15, 10, 4), rnorm(15, 12, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 2 602.3 301.15 50.811 <2e-16 ***
water 1 39.6 39.62 6.685 0.0105 *  
sunlight:water 2 15.1 7.56 1.275 0.2819    
Residuals 174 1031.3 5.93                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Zo interpreteert u het ANOVA-resultaat:

• De p-waarde geassocieerd met zonlicht is <2e-16 . Omdat dit getal minder dan 0,05 bedraagt, betekent dit dat blootstelling aan zonlicht een statistisch significant effect heeft op de plantengroei.
• De p-waarde geassocieerd met water is 0,0105 . Omdat dit cijfer minder dan 0,05 bedraagt, betekent dit dat de waterfrequentie ook een statistisch significant effect heeft op de plantengroei.
• De p-waarde voor de interactie tussen zonlicht en water is 0,2819 . Omdat dit cijfer niet minder dan 0,05 bedraagt, betekent dit dat er geen interactie-effect is tussen zonlicht en water.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over experimenteel ontwerp en analyse:

Een complete gids: het 2 × 2 factoriële ontwerp
Wat zijn niveaus van een onafhankelijke variabele?
Onafhankelijke of afhankelijke variabelen
Wat is een factoriële ANOVA?