7 basiskwaliteitstools

In dit artikel wordt uitgelegd wat de 7 basiskwaliteitsinstrumenten zijn. Je ontdekt daarom wat de 7 basiskwaliteitstools zijn en waar elk type kwaliteitstool voor gebruikt wordt.

Wat zijn de 7 basiskwaliteitsinstrumenten?

De 7 basiskwaliteitsinstrumenten zijn:

• Verificatieblad.
• Spreidingsplot.
• Histogram.
• Pareto-diagram.
• Stratificatie.
• Het Ishikawa-diagram.
• Controlekaart.

Hieronder wordt elk van de zeven basiskwaliteitsinstrumenten nader toegelicht. Van elk ziet u ook een voorbeeld.

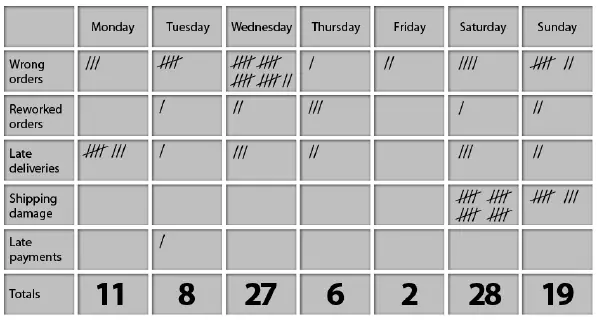
verificatieblad

Een controleblad is een tabelblad dat wordt gebruikt om gegevens van een proces vast te leggen. Met andere woorden, een controleblad is een sjabloon dat wordt gebruikt om een proces te observeren en waargenomen verschijnselen vast te leggen zodra ze zich voordoen.

Een controleblad kan bijvoorbeeld worden gebruikt om verschillende defecten in gefabriceerde eenheden vast te leggen, zodat een operator elk defect dat hij opmerkt op een controleblad noteert. Op deze manier weet u welke fouten optreden en welke het vaakst voorkomen.

De checklist kan ook een checklist , controleblad of controleblad worden genoemd.

Het belangrijkste kenmerk van een controleblad is dat gegevens worden vastgelegd door markeringen aan te brengen. Een controleblad is dus vaak verdeeld in regio’s, zodat markeringen die in verschillende regio’s zijn gemaakt verschillende betekenissen hebben. De gegevens worden gelezen door de locatie en het aantal markeringen op het vel te observeren.

Bij kwaliteitsmanagement hebben controlebladen veel toepassingen, maar worden ze vooral gebruikt om elementen van een proces vast te leggen. Gegevens verzameld met een controleblad zijn nuttig voor het analyseren van procesprestaties, het identificeren van de oorzaken van defecten en het onthullen van trends of patronen.

Spreidingsplot

De scatterplot , of scatterplot , is een soort statistisch diagram waarin een set gegevens met twee variabelen wordt uitgezet op twee cartesiaanse coördinaatassen.

Daarom worden scatterplots gebruikt om de relatie tussen twee statistische variabelen te analyseren.

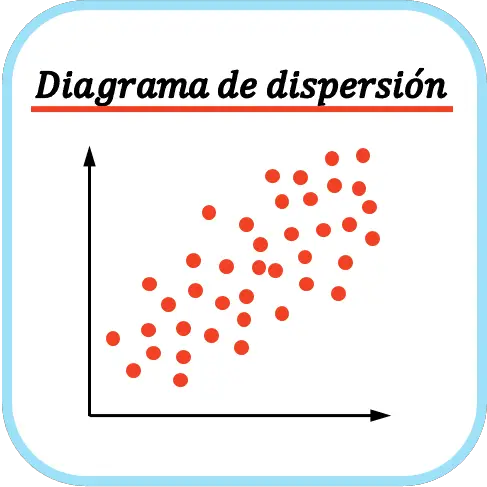
Scatterplots hebben verschillende namen, zoals „correlatiediagram“ of „scatterplot“ .

Histogram

Een histogram is een type statistisch diagram waarin een reeks statistische gegevens wordt weergegeven door rechthoekige balken, zodat elke staaf in het histogram evenredig is aan de overeenkomstige frequentie.

Histogrammen worden gebruikt om continue variabelen in een grafiek weer te geven, zoals het gewicht van een statistische steekproef. Bovendien kunt u met een histogram snel de vorm van een verdeling visualiseren.

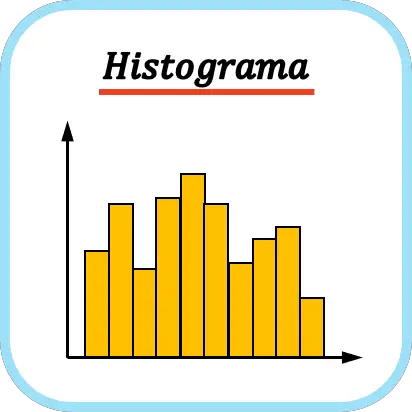
Elke staaf in een frequentiehistogram heeft een breedte die evenredig is met de breedte van het interval en een hoogte die evenredig is met de frequentie van het interval.

Pareto-diagram

Het Pareto-diagram is een type statistisch diagram waarin een reeks gegevens wordt weergegeven door balken in aflopende volgorde. Bovendien worden cumulatieve percentages grafisch weergegeven op een Pareto-diagram met behulp van een frequentiepolygoon.

Het Pareto-diagram wordt gebruikt om een probleem te analyseren en de belangrijkste oorzaken ervan te bepalen. In feite is de Pareto-grafiek de basis van het Pareto-principe, we zullen hieronder zien waaruit deze statistische regel bestaat.

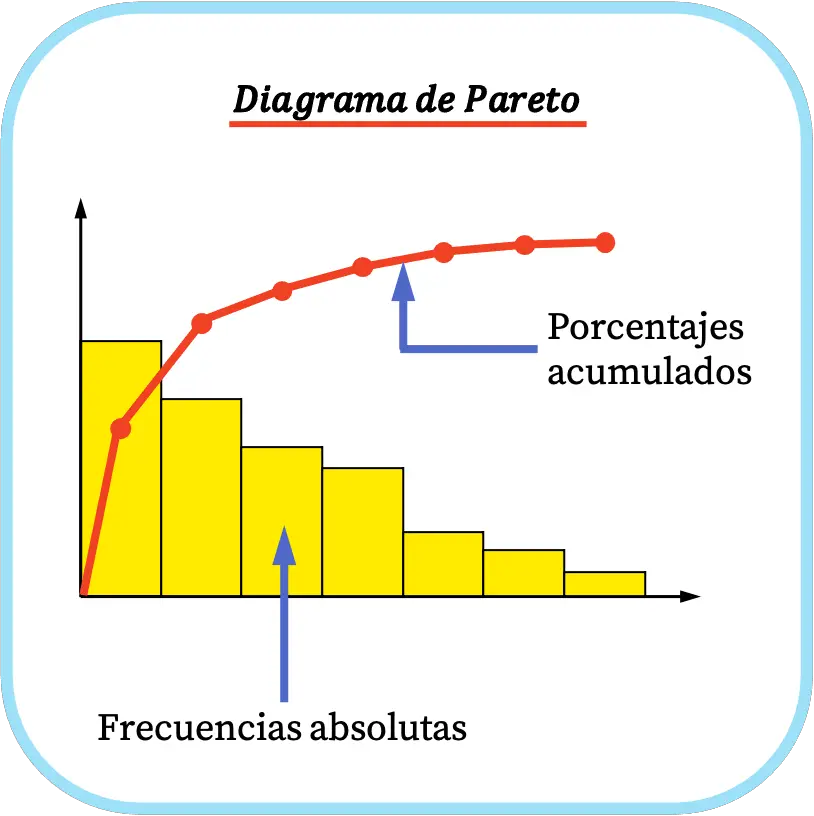
De Pareto-grafiek staat ook bekend als de gesloten curve of ABC-verdeling en is uitgevonden door de Italiaanse econoom Vilfredo Pareto.

Stratificatie

Stratificatie bestaat uit het classificeren van een reeks gegevens in verschillende lagen of groepen. Stratificatie is dus gebaseerd op het verdelen van informatie in groepen met gemeenschappelijke kenmerken om deze beter te kunnen analyseren.

Diagramstratificatie wordt vaak gebruikt bij kwaliteitsbeheer, omdat hierdoor verschillende groepen op één diagram kunnen worden geanalyseerd. Bovendien kunnen de verschillende groepen visueel met elkaar worden vergeleken.

Kijk naar het volgende voorbeeld. Door stratificatie van de gegevens in het diagram kunnen we de voorbeeldgegevens beter analyseren en een andere conclusie trekken.

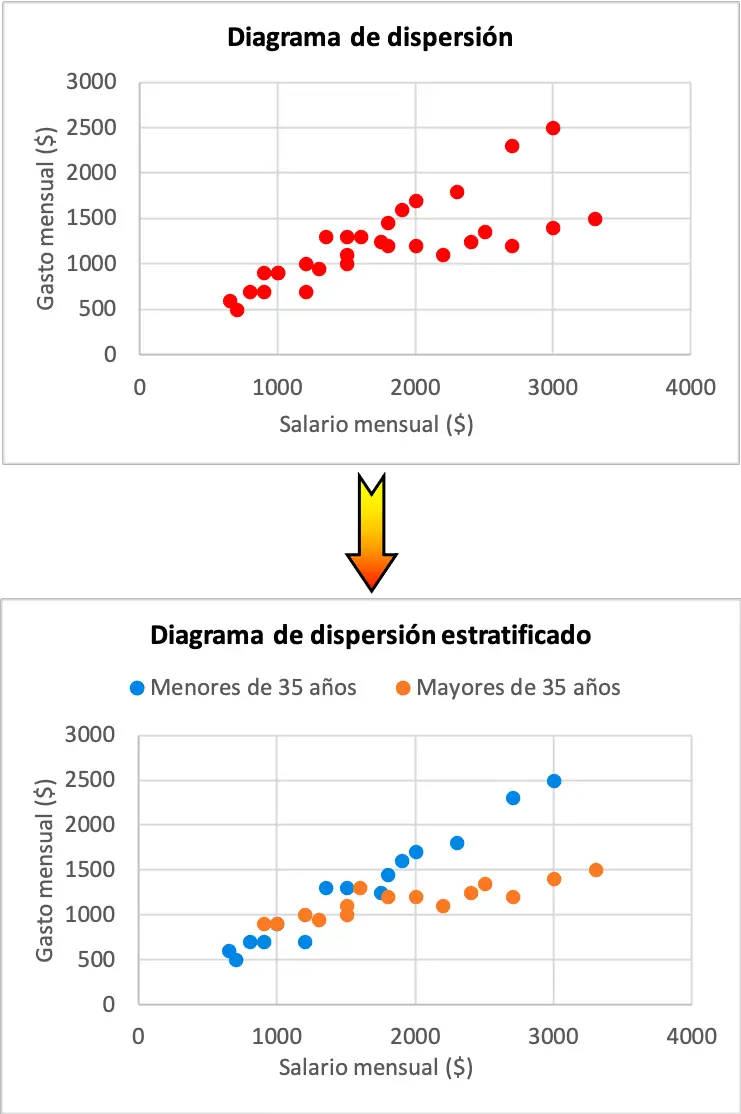
Zoals u in het bovenstaande spreidingsdiagram kunt zien, kunnen we, als we de gegevens niet stratificeren, ervan uitgaan dat de maandelijkse uitgaven van iemand rechtstreeks evenredig zijn met zijn of haar salaris.

Door de gegevens echter per strata te scheiden, kwamen we tot een andere conclusie. Mensen onder de 35 geven meer uit naarmate hun salaris stijgt, maar de variatie in de maandelijkse uitgaven per salaris is veel kleiner voor mensen boven de 35. Dit komt waarschijnlijk omdat ouderen doorgaans conservatiever zijn en meer sparen als ze overwegen om met pensioen te gaan.

Het Ishikawa-diagram

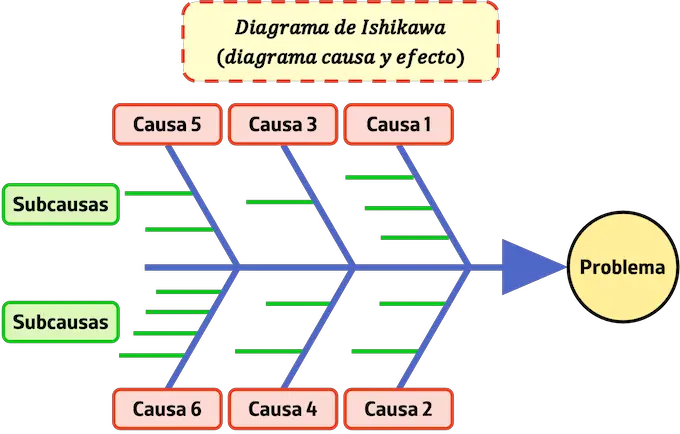
Het Ishikawa-diagram is een diagram dat wordt gebruikt om de oorzaken van een probleem te bestuderen. Concreet is het Ishikawa-diagram een diagram waarin alle oorzaken van een probleem worden weergegeven om het te analyseren en te kunnen corrigeren.

Het Ishikawa-diagram wordt vanwege zijn vorm ook wel oorzaak-gevolgdiagram , visdiagram of visgraatdiagram genoemd.

Het Ishikawa-diagram bestaat uit de volgende onderdelen:

• Viskop : in de kop van het Ishikawa-diagram staat het te bestuderen probleem geschreven.
• Botten – De botten die uit de centrale ruggengraat van de vis steken, zijn de belangrijkste oorzaken van het probleem.
• Kleine doornen : Kleine doornen die uit een andere doorn komen, vertegenwoordigen de oorzaken van een hoofdoorzaak, dus het zijn kleine oorzaken.

Merk op dat je ook doornen kunt tekenen die uit de kleine doornen komen, die de oorzaken van de kleine oorzaken zouden vertegenwoordigen. En in feite zou je dit proces voor onbepaalde tijd kunnen voortzetten totdat je de laatste oorzaak in de keten hebt bereikt.

controle kaart

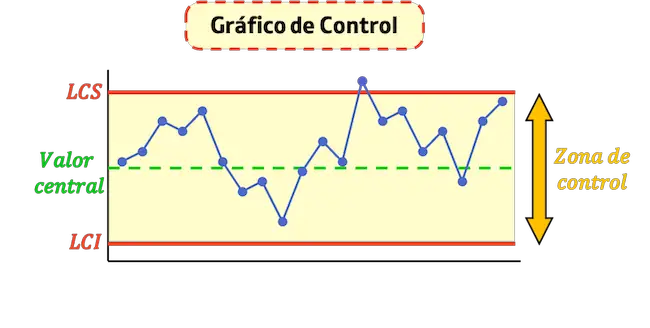
Een controlediagram (of controlediagram ) is een grafiek waarin de evolutie van een kwaliteitskenmerk wordt weergegeven. Daarom is een controlediagram een hulpmiddel voor statistische procescontrole dat wordt gebruikt om de waarde van een belangrijke parameter te monitoren.

Een controlediagram bestaat hoofdzakelijk uit drie delen: de centrale waarde, de bovenste controlelimiet en de onderste controlelimiet.

• Upper Control Limit (LCS) : dit is de lijn die de maximale waarde aangeeft die in het proces wordt geaccepteerd.
• Lower Control Limit (LCI) : Dit is de lijn die de minimumwaarde aangeeft die in het proces wordt geaccepteerd.
• Centrale waarde : Dit is de lijn die de gemiddelde waarde van het controlediagram weergeeft. Hoe dichter de punten bij deze lijn liggen, hoe stabieler het proces.

De controlekaart werd in 1920 gemaakt door Walter Andrew Shewhart en wordt daarom ook wel de Shewhart-kaart genoemd.

Bij kwaliteitsmanagement hebben controlediagrammen vele toepassingen. Een controlediagram kan bijvoorbeeld worden gebruikt om het aantal defecte eenheden in een productieproces te controleren of om de variatie in de prestaties van een financiële operatie te analyseren.