Distributie functie

In dit artikel vindt u de uitleg van de verdelingsfunctie, hoe de waarden ervan worden berekend en een praktijkvoorbeeld van de verdelingsfunctie. Bovendien kunt u de verschillen zien tussen een verdelingsfunctie en een dichtheidsfunctie.

Wat is de distributiefunctie?

De verdelingsfunctie , ook wel de cumulatieve verdelingsfunctie genoemd, is een wiskundige functie die de cumulatieve waarschijnlijkheid van een verdeling aangeeft. Dat wil zeggen dat het beeld van de verdelingsfunctie voor elke waarde gelijk is aan de waarschijnlijkheid dat de variabele die waarde of een lagere waarde aanneemt.

De cumulatieve distributiefunctie kan ook worden aangeduid met het acroniem FDA, hoewel het gebruikelijke symbool de hoofdletter F is.

De verdelingsfunctie wordt daarom gedefinieerd door de volgende formule:

Hoe de verdelingsfunctie te berekenen

Vervolgens leggen we uit hoe je de waarde van de verdelingsfunctie kunt berekenen, afhankelijk van het feit of de kansverdeling discreet of continu is.

Discrete doos

Als de willekeurige variabele discreet is, is de cumulatieve verdelingsfunctie gelijk aan de som van de kansen van alle waarden gelijk aan of kleiner dan x .

Goud

is de waarschijnlijkheidsfunctie die is geassocieerd met de discrete variabele.

Voortdurende zaak

Als de willekeurige variabele continu is, is de cumulatieve verdelingsfunctie equivalent aan de integraal van de dichtheidsfunctie van minus oneindig tot de betreffende waarde.

Goud

is de dichtheidsfunctie die is geassocieerd met de continue variabele.

Voorbeeld van distributiefunctie

Nu we de definitie van de distributiefunctie kennen, gaan we een praktisch stapsgewijs voorbeeld bekijken om te leren hoe we de waarde van een distributiefunctie kunnen berekenen.

• Bereken de verdelingsfunctie voor het willekeurige experiment waarbij je vier keer een munt opgooit.

Om de oefening op te lossen, moet je eerst alle kansen berekenen die verband houden met het aantal kop dat je krijgt tijdens de vier muntopgooien:

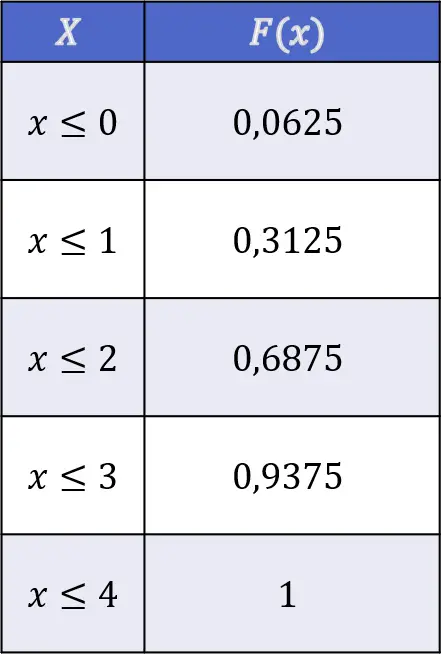
Omdat het dus een discrete variabele is, is het voor het bepalen van de afbeeldingen van de verdelingsfunctie voldoende om de kansen op te tellen bij de waarde van de betreffende variabele:

De waarden van de verdelingsfunctie van het omdraaien van het hoofd door het opgooien van vier onafhankelijke munten zijn dus als volgt:

Eigenschappen van de verdelingsfunctie

Ongeacht het type variabele heeft de verdelingsfunctie altijd de volgende eigenschappen:

• De waarde van de cumulatieve verdelingsfunctie ligt tussen 0 en 1.

• De limiet van een verdelingsfunctie waarbij x naar oneindig neigt, is gelijk aan 1.

• Aan de andere kant is de limiet van een verdelingsfunctie wanneer x min oneindig nadert nul.

• Door zijn kenmerken is de distributiefunctie monotoon en niet-afnemend.

• Verder, als

  

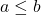
  aan de volgende vergelijkingen is voldaan.

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

Verdelingsfunctie en dichtheidsfunctie

Ten slotte zullen we zien wat het verschil is tussen de verdelingsfunctie en de dichtheidsfunctie, aangezien deze twee statistische begrippen vaak met elkaar worden verward.

Het verschil tussen de verdelingsfunctie en de dichtheidsfunctie is het type waarschijnlijkheid dat ze definiëren. De dichtheidsfunctie beschrijft de waarschijnlijkheid dat de variabele een bepaalde waarde aanneemt, terwijl de verdelingsfunctie de cumulatieve waarschijnlijkheid van de variabele beschrijft.

Dat wil zeggen dat de verdelingsfunctie wordt gebruikt om de waarschijnlijkheid te berekenen dat de variabele gelijk is aan of kleiner is dan een bepaalde waarde.

Merk op dat de dichtheidsfunctie alleen verwijst naar continue variabelen, dus dit onderscheid is alleen zinvol als de bestudeerde variabele continu is.

Merk op hoe de grafische weergave van de verdelingsfunctie verandert vergeleken met de dichtheidsfunctie van een variabele die een normale verdeling volgt met een gemiddelde van 1 en een standaardafwijking van 0,5:

Zie het volgende artikel voor meer informatie over de dichtheidsfunctie: