Waarschijnlijkheidsfunctie

In dit artikel wordt uitgelegd wat waarschijnlijkheidsfuncties zijn. Zo vindt u de betekenis van een waarschijnlijkheidsfunctie, de eigenschappen ervan en een concreet voorbeeld van het berekenen van een waarschijnlijkheidsfunctie. Bovendien worden de verschillen tussen een waarschijnlijkheidsfunctie en andere soorten probabilistische functies gepresenteerd.

Wat is een waarschijnlijkheidsfunctie?

Een waarschijnlijkheidsfunctie , ook wel waarschijnlijkheidsmassafunctie genoemd, is een wiskundige functie die de waarschijnlijkheid beschrijft dat een discrete willekeurige variabele een bepaalde waarde aanneemt.

Dat wil zeggen dat een waarschijnlijkheidsfunctie de waarschijnlijkheid retourneert die bij een discrete variabele hoort en exact gelijk is aan een waarde.

De kans dat je een willekeurig getal gooit bij het gooien van een dobbelsteen is bijvoorbeeld 1/6 (een dobbelsteen heeft zes zijden), daarom zal de waarschijnlijkheidsfunctie die bij deze steekproefruimte hoort, gelijk zijn aan 1/6 voor n, ongeacht welke waarde.

Eigenschappen van de waarschijnlijkheidsfunctie

Waarschijnlijkheidsfuncties hebben de volgende eigenschappen:

• Waarschijnlijkheden kunnen niet negatief zijn, dus de waarschijnlijkheidsfunctie is nul of positief voor elke waarde van x.

• Op dezelfde manier is de maximale waarschijnlijkheid één, wat betekent dat de gebeurtenis altijd zal plaatsvinden. Daarom is de maximale waarde van de waarschijnlijkheidsfunctie gelijk aan 1.

• Ten slotte geeft de som van alle waarden van een waarschijnlijkheidsfunctie 1, aangezien dit de som is van alle kansen in de steekproefruimte.

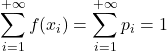
Voorbeeld van waarschijnlijkheidsfunctie

Nu we de definitie en kenmerken van de waarschijnlijkheidsfunctie kennen, laten we een voorbeeld van dit type probabilistische functie bekijken.

• Bereken de kansen om 0, 1, 2, 3 en 4 keer kop te krijgen door vier onafhankelijke muntopgooien te maken. Teken vervolgens de gevonden waarschijnlijkheidsfunctie.

Allereerst moeten we de waarschijnlijkheid berekenen dat we kop krijgen. Om dit te doen, moeten we de mogelijke gevallen delen door het totale aantal gevallen. U kunt de berekening van alle kansen in de volgende tabel zien:

En zodra we alle kansen hebben berekend, kunnen we de waarden van de waarschijnlijkheidsfunctie in een grafiek weergeven:

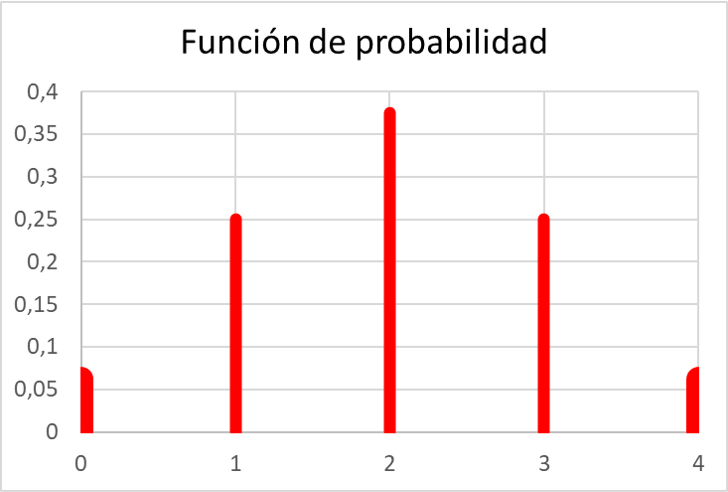
Zoals je kunt zien voldoet de probabilistische functie in de oefening aan alle eigenschappen van waarschijnlijkheidsfuncties, aangezien al zijn waarden tussen 0 en 1 liggen en bovendien de som van al zijn waarden gelijk is aan 1.

Waarschijnlijkheidsfunctie en dichtheidsfunctie

In deze sectie zullen we het verschil zien tussen de waarschijnlijkheidsfunctie en de dichtheidsfunctie, aangezien het twee soorten probabilistische functies zijn die hetzelfde doel hebben maar in verschillende gevallen worden gebruikt.

Het verschil tussen de waarschijnlijkheidsfunctie en de dichtheidsfunctie is het type variabele waarvoor de kansen beschrijven. De waarschijnlijkheidsfunctie wordt gebruikt om de kansen van een discrete variabele te definiëren, terwijl de dichtheidsfunctie wordt gebruikt om de kansen van een continue variabele te definiëren.

Afhankelijk van de variabele wordt dus een waarschijnlijkheidsfunctie of een dichtheidsfunctie gebruikt.

Voor meer informatie over de dichtheidsfunctie klikt u op de volgende link:

Waarschijnlijkheidsfunctie en verdelingsfunctie

Het verschil tussen een waarschijnlijkheidsfunctie en een verdelingsfunctie is het type waarschijnlijkheid dat ze definiëren. De waarschijnlijkheidsfunctie geeft de waarschijnlijkheid aan dat de variabele een bepaalde waarde aanneemt, terwijl de verdelingsfunctie de cumulatieve waarschijnlijkheid van de variabele beschrijft.

Daarom wordt de verdelingsfunctie berekend op basis van de waarschijnlijkheidsfunctie.

In de volgende link kun je bijvoorbeeld de berekening zien van de verdelingsfunctie om kop te krijgen uit vier opgooien van munten, gebaseerd op de waarschijnlijkheidsfunctie die je in de bovenstaande oefening hebt gevonden.