Wederzijds inclusieve of wederzijds uitsluitende evenementen

Twee gebeurtenissen sluiten elkaar uit als ze niet tegelijkertijd kunnen plaatsvinden.

Stel bijvoorbeeld dat gebeurtenis A de gebeurtenis is waarbij een dobbelsteen op een even getal terechtkomt, en gebeurtenis B de gebeurtenis is dat een dobbelsteen op een oneven getal terechtkomt.

We definiëren de voorbeeldruimte voor evenementen als volgt:

• EEN = {2, 4, 6}
• B = {1, 3, 5}

Merk op dat er geen overlap is tussen de twee bemonsterde ruimtes. Gebeurtenissen A en B sluiten elkaar dus wederzijds uit, omdat ze niet allebei tegelijkertijd kunnen plaatsvinden. Het getal waarop een dobbelsteen valt, kan niet zowel even als oneven zijn.

Omgekeerd zijn twee gebeurtenissen wederzijds inclusief als ze tegelijkertijd kunnen plaatsvinden.

Laat bijvoorbeeld gebeurtenis C de gebeurtenis zijn waarbij een dobbelsteen op een even getal terechtkomt en laat gebeurtenis D de gebeurtenis zijn waarbij een dobbelsteen op een getal groter dan 3 terechtkomt.

We definiëren de voorbeeldruimte voor evenementen als volgt:

• C = {2, 4, 6}
• d = {4, 5, 6}

Merk op dat er een overlap is tussen de twee bemonsterde ruimtes. Gebeurtenissen C en D omvatten dus beide elkaar, omdat ze tegelijkertijd kunnen plaatsvinden. Het is mogelijk dat de dobbelstenen op een even getal groter dan 3 terechtkomen.

Waarschijnlijkheden van gebeurtenissen

Als twee gebeurtenissen elkaar uitsluiten, is de kans dat beide plaatsvinden nul.

Beschouw bijvoorbeeld de twee voorbeeldruimten voor gebeurtenissen A en B hierboven:

• EEN = {2, 4, 6}
• B = {1, 3, 5}

Omdat er geen overlap is in de monsterruimten, zouden we zeggen P(A en B) = 0 .

Maar als twee gebeurtenissen elkaar wederzijds omvatten , zal de waarschijnlijkheid dat ze allebei plaatsvinden een getal groter dan nul zijn.

Beschouw bijvoorbeeld de twee voorbeeldruimten voor gebeurtenissen C en D eerder:

• C = {2, 4, 6}
• d = {4, 5, 6}

Omdat er zes mogelijke getallen zijn waarop de dobbelstenen kunnen landen en twee van die getallen (4 en 6) bij zowel de gebeurtenissen C als D horen, berekenen we P(C en D) als 2/6, oftewel 1/3 .

Bekijk wederzijds inclusieve en wederzijds exclusieve evenementen

We gebruiken vaak Venn-diagrammen om de kansen die verband houden met gebeurtenissen te visualiseren.

Als twee gebeurtenissen elkaar uitsluiten, overlappen ze elkaar helemaal niet in een Venn-diagram:

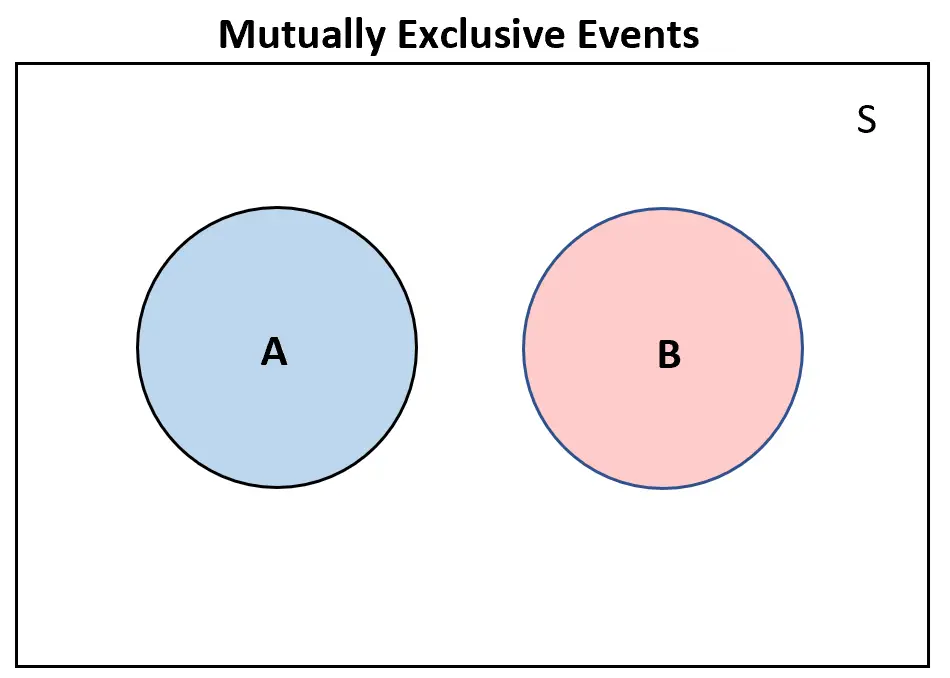
Omgekeerd, als twee gebeurtenissen elkaar wederzijds omvatten , zou er op zijn minst enige overlap zijn in het Venn-diagram:

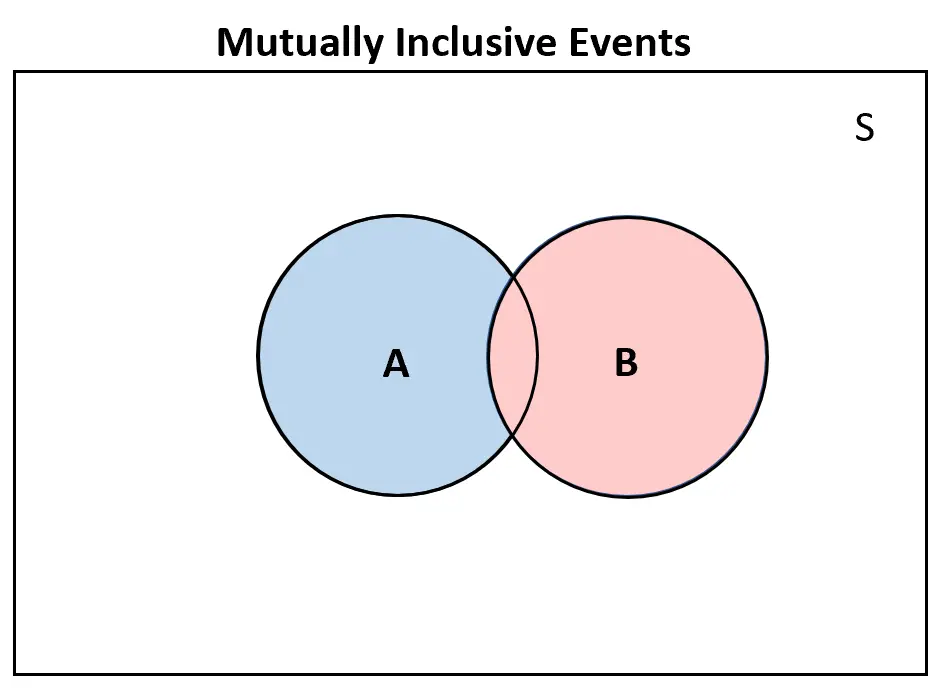
Aanvullende bronnen

Een inleiding tot theoretische waarschijnlijkheid
De algemene regel van vermenigvuldiging
Wat zijn onsamenhangende gebeurtenissen?