De stelling van chebyshev

Dit artikel legt uit wat de stelling van Chebyshev is. Hier vind je de Chebyshev-stellingformule, een opgeloste oefening en daarnaast een online Chebyshev-stellingcalculator. Ten slotte laat het het verschil zien tussen de stelling van Chebyshev en de empirische regel.

Wat is de stelling van Chebyshev?

De stelling van Chebyshev , ook bekend als de ongelijkheid van Chebyshev , is een statistische regel die wordt gebruikt om de waarschijnlijkheid te berekenen dat een waarde van een willekeurige variabele binnen een bepaalde afstand van het gemiddelde ligt.

Met andere woorden: in de statistiek wordt de stelling van Chebyshev gebruikt om de waarschijnlijkheid te bepalen dat een waarde binnen een betrouwbaarheidsinterval ligt.

Bovendien wordt de stelling van Chebyshev ook gebruikt om andere statistische stellingen te bewijzen, zoals de wet van de grote getallen.

Hoewel de stelling van Chebyshev voor het eerst werd geformuleerd door de Fransman Irénée-Jules Bienaymé, wordt de stelling zo genoemd omdat deze in 1867 door de Rus Pafnuty Chebushev is ontstaan.

Formule van de stelling van Chebyshev

De stelling van Chebyshev zegt dat de waarschijnlijkheid dat een waarde gelijk is aan k standaardafwijkingen van het gemiddelde groter is dan of gelijk is aan één minus de verhouding van één gedeeld door k kwadraat.

Daarom is de formule voor de stelling van Chebyshev als volgt:

Goud

is de waarde van de willekeurige variabele,

het rekenkundig gemiddelde van de variabele,

de standaarddeviatie en

het aantal standaardafwijkingen van het gemiddelde waarover de waarschijnlijkheid moet worden berekend.

Merk op dat deze formule alleen kan worden gebruikt als het aantal standaarddeviaties waarop de berekening wordt uitgevoerd groter is dan 1, of met andere woorden, als k groter is dan 1.

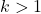U kunt de onderstaande online Chebyshev-stellingcalculator gebruiken om de waarschijnlijkheid te berekenen.

Voorbeeld van de stelling van Chebyshev

Zodra we de definitie van de stelling van Chebyshev hebben gezien en wat de formule ervan is, is hier een opgelost voorbeeld van deze statistische stelling om het concept beter te begrijpen.

• Als de cijfers behaald in de cursusstatistieken van een universiteit worden gedefinieerd door een verdeling met een gemiddelde van 65 en een standaarddeviatie van 10, welk percentage studenten behaalde dan een cijfer tussen 50 en 80?

Om dit probleem op te lossen, moeten we de formule van de stelling van Chebyshev toepassen. We moeten echter eerst bepalen hoeveel standaarddeviaties de waarden 50 en 80 afwijken van het gemiddelde van de variabele. Om dit te doen, hoeven we alleen maar de volgende berekening uit te voeren:

Daarom komen de waarden 50 en 80 overeen met respectievelijk 1,5 standaardafwijkingen van het onderste en bovenste gemiddelde. We gebruiken daarom de formule van de stelling van Chebysheva met k = 1,5:

Zo behaalde minstens 55,56% van de studenten een cijfer tussen 50 en 80.

Chebyshev’s Stellingcalculator

Voer het aantal standaarddeviaties in tussen de betreffende waarden en het gemiddelde (k) en klik vervolgens op ‘Berekenen’. De rekenmachine retourneert dan de minimale waarschijnlijkheid van het betrouwbaarheidsinterval.

U moet het aantal standaardafwijkingen invoeren, waarbij u de punt als decimaalteken gebruikt.

Stelling en vuistregel van Chebyshev

Twee nauw verwante concepten in de statistiek zijn de stelling van Chebyshev en de empirische regel, aangezien beide worden gebruikt om de waarschijnlijkheid van betrouwbaarheidsintervallen te berekenen.

Het verschil tussen de stelling van Chebyshev en de empirische regel is dat de stelling van Chebyshev op elk type verdeling kan worden gebruikt, terwijl de empirische regel alleen geldig is voor een normale verdeling.

Het gebruik van de stelling van Chebyshev is daarom breder, maar de empirische regel levert preciezere resultaten op voor een normale verdeling.

Klik hier om te zien wat de vuistregel precies is: