Correlatie versus regressie: wat is het verschil?

Correlatie en regressie zijn twee verwante, maar niet geheel dezelfde, statistische termen.

In deze tutorial geven we een korte uitleg van beide termen en leggen we uit hoe ze vergelijkbaar en verschillend zijn.

Wat is correlatie?

Correlatie meet de lineaire associatie tussen twee variabelen, x en y . Het heeft een waarde tussen -1 en 1 waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

Stel dat we bijvoorbeeld de volgende dataset hebben die twee variabelen bevat: (1) Gestudeerde uren en (2) Examenscores ontvangen voor 20 verschillende studenten:

Als we een spreidingsdiagram zouden maken van de bestudeerde uren versus de examenresultaten, zou het er zo uitzien:

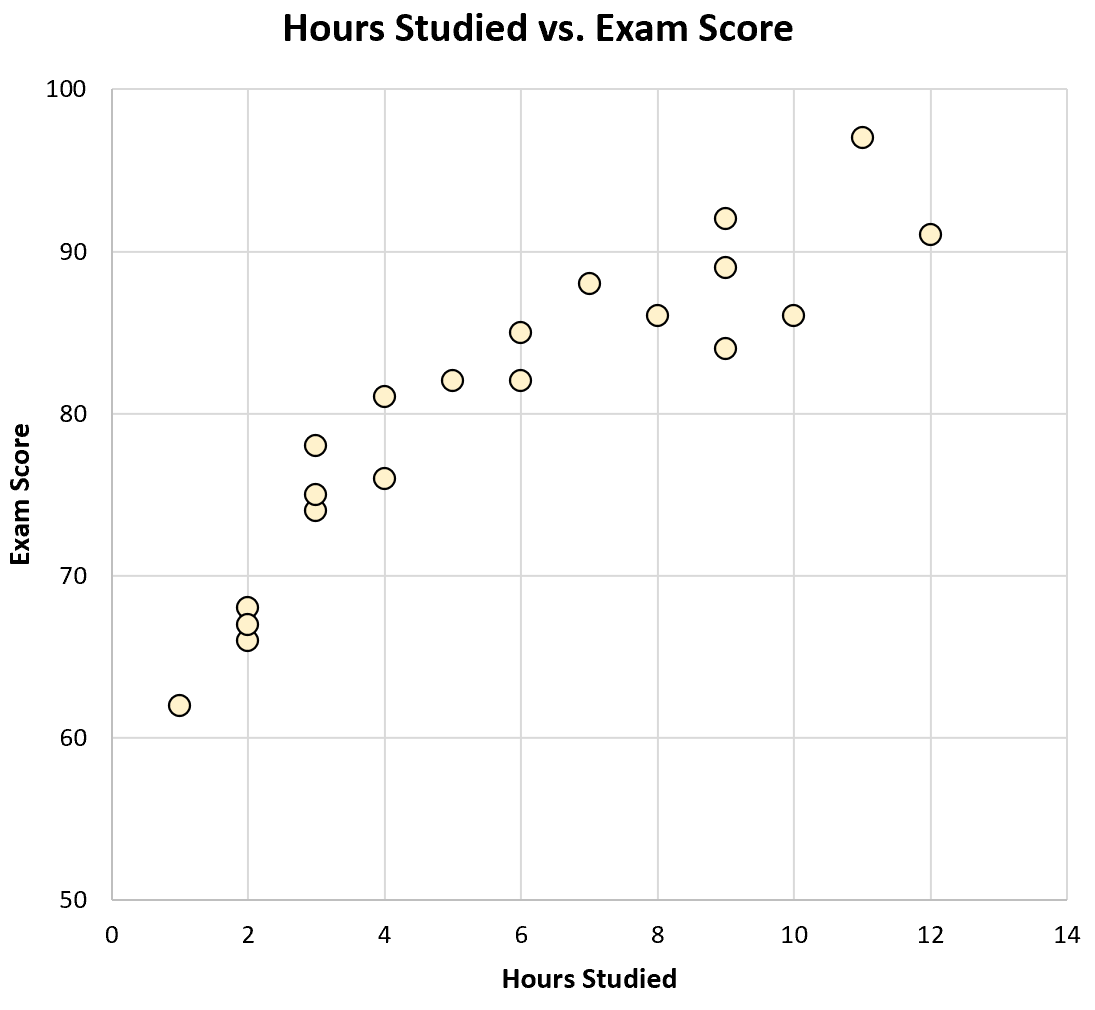
Alleen al door naar de grafiek te kijken, kunnen we zien dat studenten die meer studeren doorgaans beter presteren op examens. Met andere woorden: we kunnen visueel zien dat er een positieve correlatie bestaat tussen de twee variabelen.

Met behulp van een rekenmachine kunnen we zien dat de correlatie tussen deze twee variabelen r = 0,915 is. Omdat deze waarde dicht bij 1 ligt, bevestigt dit dat er een sterke positieve correlatie bestaat tussen de twee variabelen.

Wat is regressie?

Regressie is een methode die we kunnen gebruiken om te begrijpen hoe het veranderen van de waarden van de variabele x de waarden van de variabele y beïnvloedt.

Een regressiemodel gebruikt één variabele, x , als voorspellende variabele en de andere variabele, y , alsresponsvariabele . Vervolgens wordt een vergelijking gevonden met de volgende vorm die de relatie tussen de twee variabelen het beste beschrijft:

ŷ = _b0 + _b1 x

Goud:

• ŷ: de voorspelde waarde van de responsvariabele
• b ₀ : De ordinaat bij de oorsprong (de waarde van y wanneer x gelijk is aan nul)
• b ₁ : De regressiecoëfficiënt (de gemiddelde toename in y voor een toename van één eenheid in x)
• x: de waarde van de voorspellende variabele

Kijk bijvoorbeeld eens naar onze vorige dataset:

Met behulp van een lineaire regressiecalculator ontdekken we dat de volgende vergelijking de relatie tussen deze twee variabelen het beste beschrijft:

Voorspelde examenscore = 65,47 + 2,58*(uren gestudeerd)

De manier om deze vergelijking te interpreteren is:

• De voorspelde examenscore voor een student die nul uur studeert is 65,47 .
• De gemiddelde stijging van de examenscore bij een extra uur studeren bedraagt 2,58 .

We kunnen deze vergelijking ook gebruiken om te voorspellen welke score een student zal behalen op basis van het aantal gestudeerde uren.

Een student die bijvoorbeeld 6 uur studeert, zou een cijfer van 80,95 moeten krijgen:

Voorspelde examenscore = 65,47 + 2,58*(6) = 80,95 .

We kunnen deze vergelijking ook uitzetten als een lijn op een spreidingsdiagram:

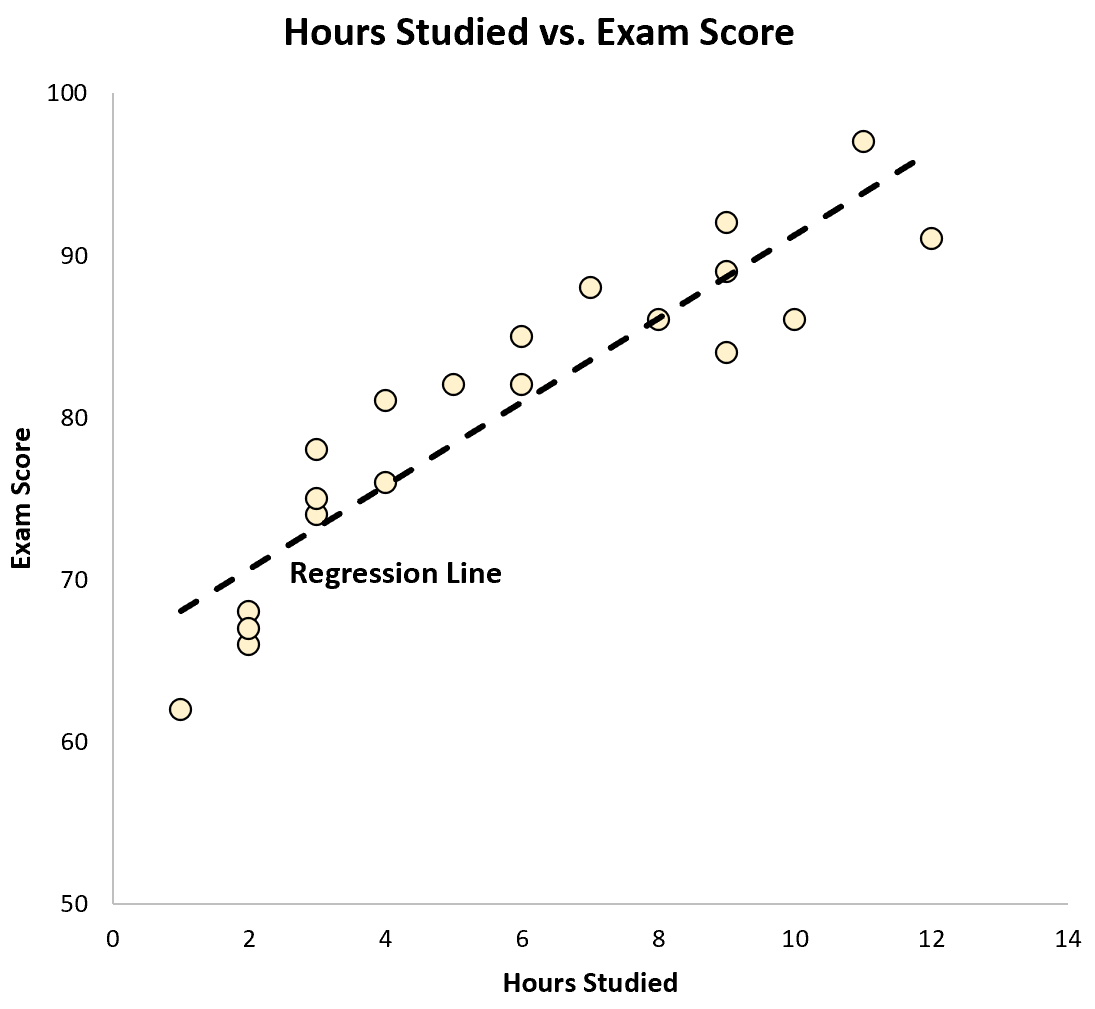
We kunnen zien dat de regressielijn vrij goed bij de gegevens past.

Bedenk eerder dat de correlatie tussen deze twee variabelen r = 0,915 was. Het blijkt dat we deze waarde kunnen kwadrateren en een getal kunnen krijgen dat ‚r kwadraat‘ wordt genoemd en dat het totale aandeel van de variantie in de responsvariabele beschrijft dat kan worden verklaard door de voorspellende variabele.

In dit voorbeeld is r ² = 0,915 ² = 0,837 . Dit betekent dat 83,7% van de variatie in examenscores kan worden verklaard door het aantal gestudeerde uren.

Correlatie versus regressie: overeenkomsten en verschillen

Hier is een samenvatting van de overeenkomsten en verschillen tussen correlatie en regressie:

Overeenkomsten:

• Beide kwantificeren de richting van een relatie tussen twee variabelen.
• Beide kwantificeren de sterkte van een verband tussen twee variabelen.

Verschillen:

• Regressie is in staat een oorzaak-gevolgrelatie tussen twee variabelen aan te tonen. Correlatie doet dat niet.
• Regressie kan een vergelijking gebruiken om de waarde van één variabele te voorspellen, gebaseerd op de waarde van een andere variabele. Correlatie doet dat niet.
• Regressie gebruikt een vergelijking om de relatie tussen twee variabelen te kwantificeren. Correlatie gebruikt een enkel getal.

Aanvullende bronnen

De volgende tutorials bieden een uitgebreidere uitleg van de onderwerpen die in dit artikel worden behandeld.

Een inleiding tot de Pearson-correlatiecoëfficiënt
Een inleiding tot eenvoudige lineaire regressie
Eenvoudige lineaire regressiecalculator
Wat is een goede R-kwadraatwaarde?