Hoe dummyvariabelen te gebruiken in regressieanalyse
Lineaire regressie is een methode die we kunnen gebruiken om de relatie tussen een of meer voorspellende variabelen en eenresponsvariabele te kwantificeren.
Over het algemeen gebruiken we lineaire regressie met kwantitatieve variabelen . Dit worden ook wel ‘numerieke’ variabelen genoemd. Dit zijn variabelen die een meetbare hoeveelheid vertegenwoordigen. Voorbeelden zijn onder meer:
- Aantal vierkante meter in een huis
- Bevolkingsomvang van een stad
- Leeftijd van een individu
Soms willen we echter categorische variabelen gebruiken als voorspellende variabelen. Dit zijn variabelen die namen of labels aannemen en in categorieën kunnen vallen. Voorbeelden zijn onder meer:
- Oogkleur (bijvoorbeeld “blauw”, “groen”, “bruin”)
- Geslacht (bijvoorbeeld “man”, “vrouw”)
- Burgerlijke staat (bijvoorbeeld ‘getrouwd’, ‘single’, ‘gescheiden’)
Bij het gebruik van categorische variabelen heeft het geen zin om zomaar waarden als 1, 2, 3 toe te wijzen aan waarden als ‘blauw’, ‘groen’ en ‘bruin’, omdat het geen zin heeft om te zeggen dat groen is dubbel. zo kleurrijk als blauw of bruin is drie keer kleurrijker dan blauw.
In plaats daarvan is de oplossing het gebruik van dummyvariabelen . Dit zijn variabelen die we specifiek voor regressieanalyse maken en die een van de twee waarden kunnen aannemen: nul of één.
Dummyvariabelen: numerieke variabelen die in regressieanalyse worden gebruikt om categorische gegevens weer te geven die slechts één van twee waarden kunnen aannemen: nul of één.
Het aantal dummyvariabelen dat we moeten creëren is gelijk aan k -1 waarbij k het aantal verschillende waarden is dat de categorische variabele kan aannemen.
De volgende voorbeelden illustreren hoe u dummyvariabelen voor verschillende gegevenssets maakt.
Voorbeeld 1: Maak een dummyvariabele met slechts twee waarden
Stel dat we de volgende dataset hebben en geslacht en leeftijd willen gebruiken om het inkomen te voorspellen:
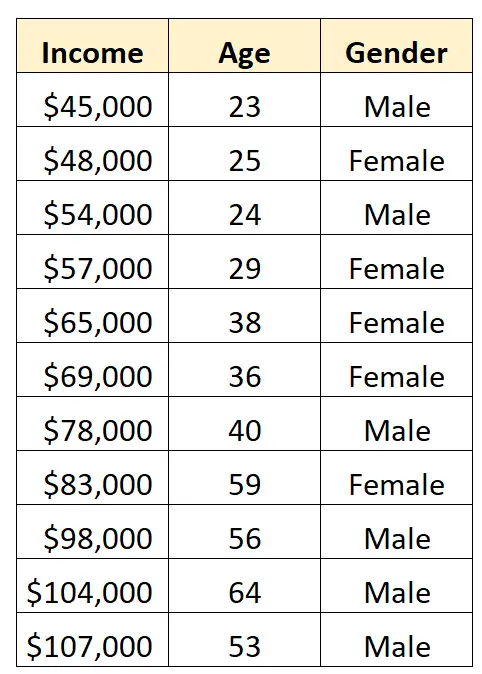
Om geslacht als voorspellende variabele in een regressiemodel te gebruiken, moeten we deze naar een dummyvariabele converteren.
Omdat dit momenteel een categorische variabele is die twee verschillende waarden kan aannemen („Male“ of „Female“), maken we eenvoudigweg k -1 = 2-1 = 1 dummyvariabele.
Om deze dummyvariabele te maken, kunnen we een van de waarden (“Male” of “Female”) kiezen om 0 weer te geven en de andere om 1 weer te geven.
Over het algemeen vertegenwoordigen we de meest voorkomende waarde meestal met een 0, wat in deze dataset ‚Man‘ zou zijn.
Hier leest u hoe u geslacht omzet in een dummyvariabele:
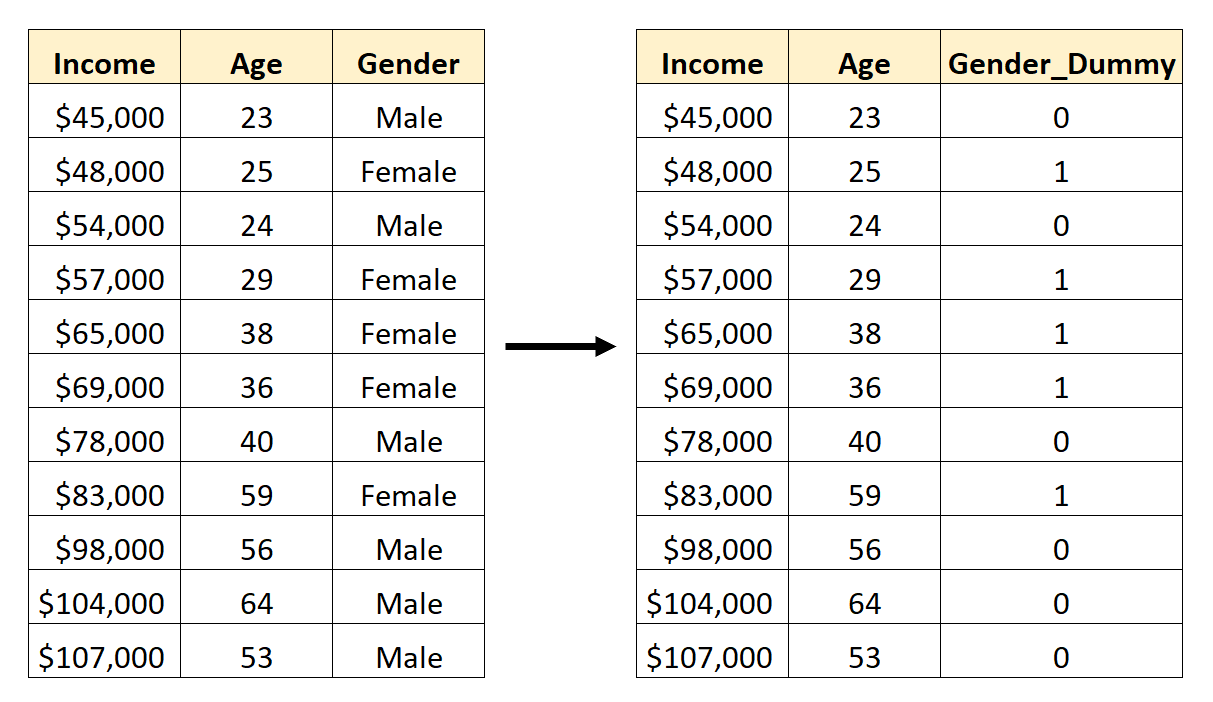
We zouden dan Age en Gender_Dummy kunnen gebruiken als voorspellende variabelen in een regressiemodel.
Voorbeeld 2: Maak een dummyvariabele met meerdere waarden
Stel dat we de volgende gegevensset hebben en de burgerlijke staat en leeftijd willen gebruiken om het inkomen te voorspellen:

Om de burgerlijke staat als voorspellende variabele in een regressiemodel te gebruiken, moeten we deze omzetten in een dummyvariabele.
Omdat dit momenteel een categorische variabele is die drie verschillende waarden kan aannemen („Single“, „Married“ of „Divorced“), moeten we k -1 = 3-1 = 2 dummyvariabelen maken.
Om deze dummyvariabele te maken, kunnen we ‚Single‘ als basiswaarde laten staan, aangezien deze het vaakst voorkomt. Dus hier is hoe we de burgerlijke staat zouden omzetten in dummyvariabelen:

We zouden dan Leeftijd , Getrouwd en Gescheiden kunnen gebruiken als voorspellende variabelen in een regressiemodel.
Hoe regressie-uitvoer met dummyvariabelen te interpreteren
Stel dat we een meervoudig lineair regressiemodel passen met behulp van de gegevensset uit het vorige voorbeeld, met Leeftijd , Getrouwd en Gescheiden als voorspellende variabelen en Inkomen als responsvariabele.
Hier is het resultaat van de regressie:
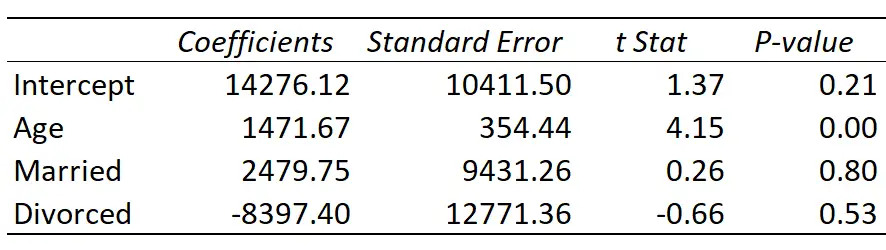
De gepaste regressielijn wordt gedefinieerd als:
Inkomen = 14.276,21 + 1.471,67*(Leeftijd) + 2.479,75*(Getrouwd) – 8.397,40*(Gescheiden)
We kunnen deze vergelijking gebruiken om het geschatte inkomen van een persoon te vinden op basis van zijn leeftijd en burgerlijke staat. Een persoon van 35 jaar en getrouwd zou bijvoorbeeld een geschat inkomen hebben van $ 68.264 :
Inkomen = 14.276,21 + 1.471,67*(35) + 2.479,75*(1) – 8.397,40*(0) = $68.264
Zo interpreteert u de regressiecoëfficiënten in de tabel:
- Intercept: Het intercept vertegenwoordigt het gemiddelde inkomen van een alleenstaande van nul jaar oud. Het is duidelijk dat je geen nuljaren kunt hebben, dus het heeft geen zin om het snijpunt op zichzelf te interpreteren in dit specifieke regressiemodel.
- Leeftijd: Elk jaar dat de leeftijd stijgt, gaat gepaard met een gemiddelde inkomensstijging van $ 1.471,67. Omdat de p-waarde (0,00) kleiner is dan 0,05, is leeftijd een statistisch significante voorspeller van het inkomen.
- Getrouwd: Een getrouwde persoon verdient gemiddeld €2.479,75 meer dan een alleenstaande. Omdat de p-waarde (0,80) niet kleiner is dan 0,05, is dit verschil niet statistisch significant.
- Gescheiden: Een gescheiden persoon verdient gemiddeld €8.397,40 minder dan een alleenstaande. Omdat de p-waarde (0,53) niet kleiner is dan 0,05, is dit verschil niet statistisch significant.
Omdat beide dummyvariabelen niet statistisch significant waren, konden we de burgerlijke staat als voorspeller uit het model verwijderen, omdat deze geen voorspellende waarde lijkt toe te voegen aan het inkomen.
Aanvullende bronnen
Kwalitatieve en kwantitatieve variabelen
De dummy-variabele val
Een regressietabel lezen en interpreteren
Een uitleg van P-waarden en statistische significantie