Wat is een unimodale verdeling? (definitie & #038; voorbeeld)
Een unimodale verdeling is een kansverdeling met een duidelijke piek.
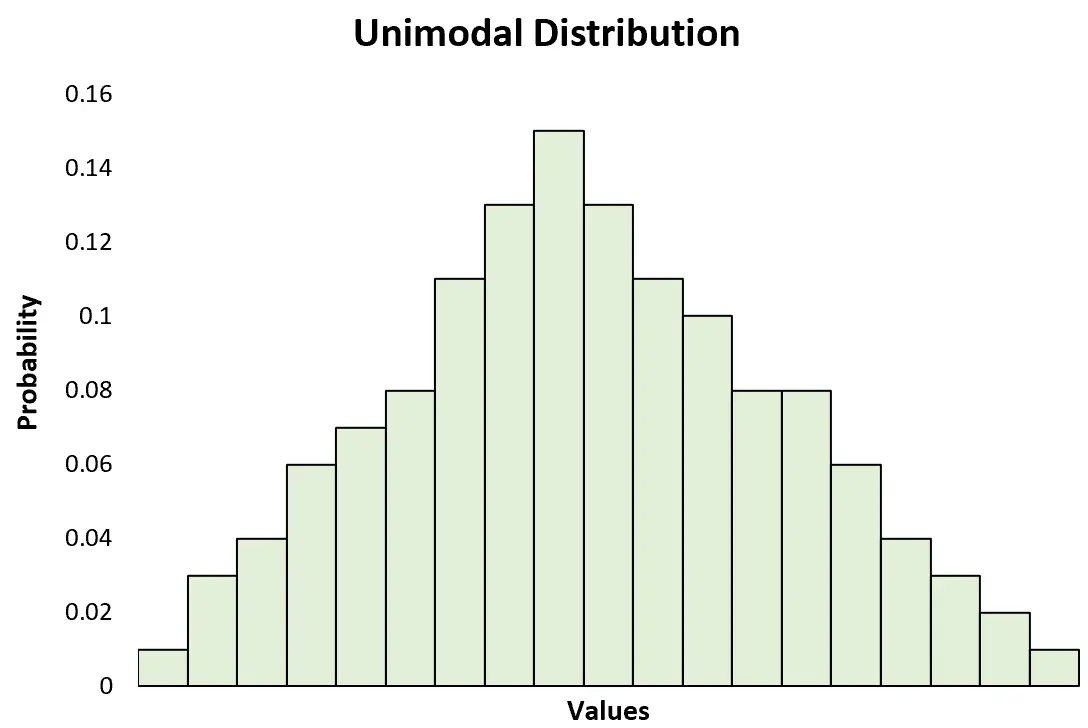
Dit staat in contrast met een bimodale verdeling , die twee duidelijke pieken kent:
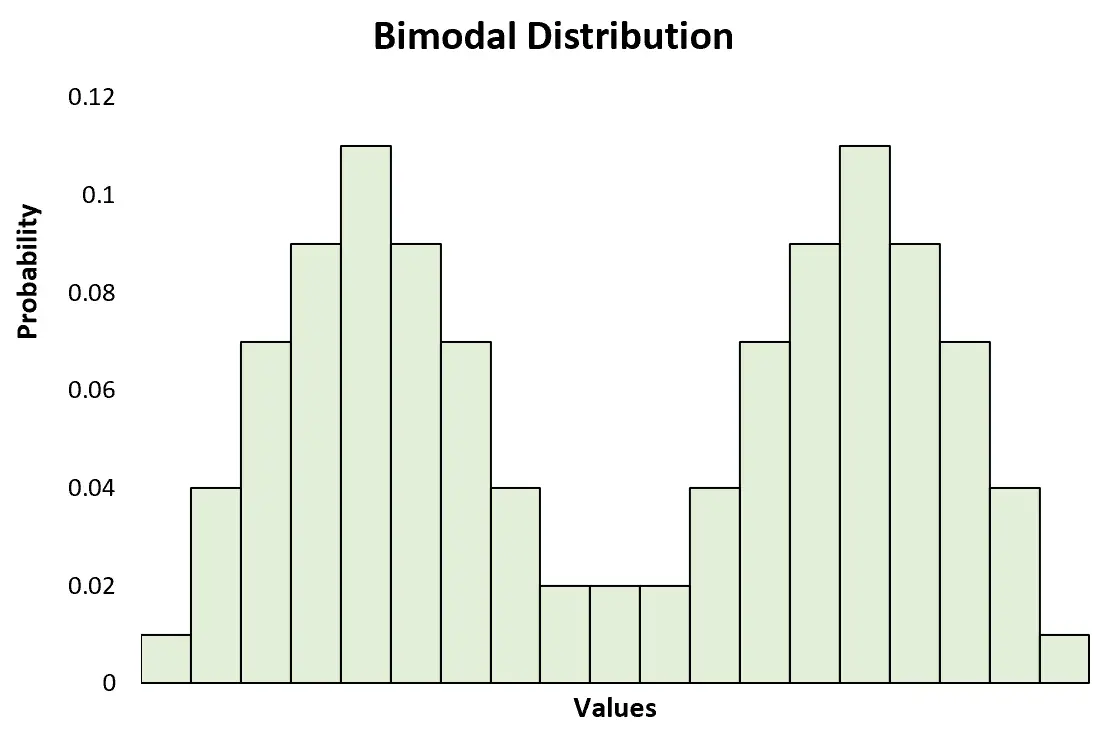
Dit staat ook in contrast met een multimodale distributie , die twee of meer pieken kent:
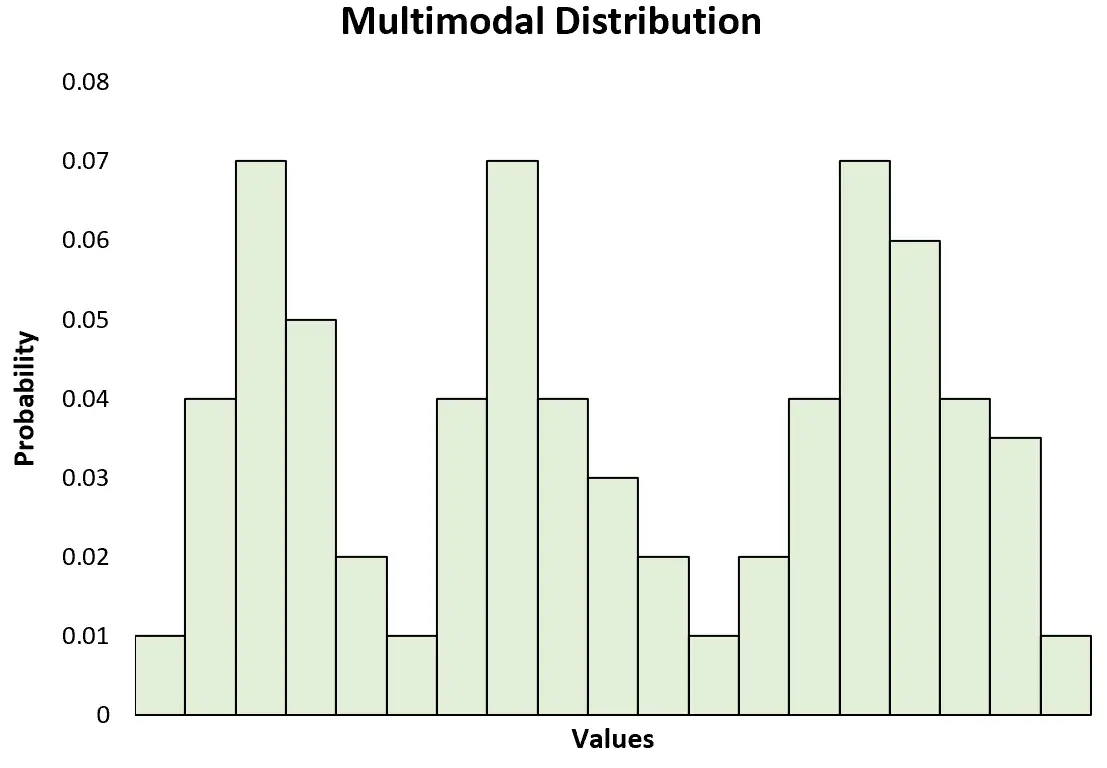
Opmerking: een bimodale distributie is slechts een specifiek type multimodale distributie.
Voorbeelden van unimodale distributies
Hier zijn enkele voorbeelden van unimodale distributies in de praktijk.
Voorbeeld 1: Geboortegewicht van baby’s
Het is bekend dat de gewichtsverdeling van pasgeborenen een unimodale verdeling volgt, met een gemiddelde van ongeveer 7,5 pond. Als we een histogram van het gewicht van baby’s maken, zien we een „piek“ van 7,5 pond, waarbij sommige baby’s meer wegen en andere minder.

Voorbeeld 2: ACT-scores
De gemiddelde ACT-score voor middelbare scholieren in de Verenigde Staten ligt rond de 21, waarbij sommige studenten lager scoren en andere hoger. Als we een histogram van ACT-scores voor alle studenten in de Verenigde Staten maken, zien we een enkele „piek“ op 21-jarige leeftijd, met hogere scores voor sommige studenten en lagere scores voor andere.
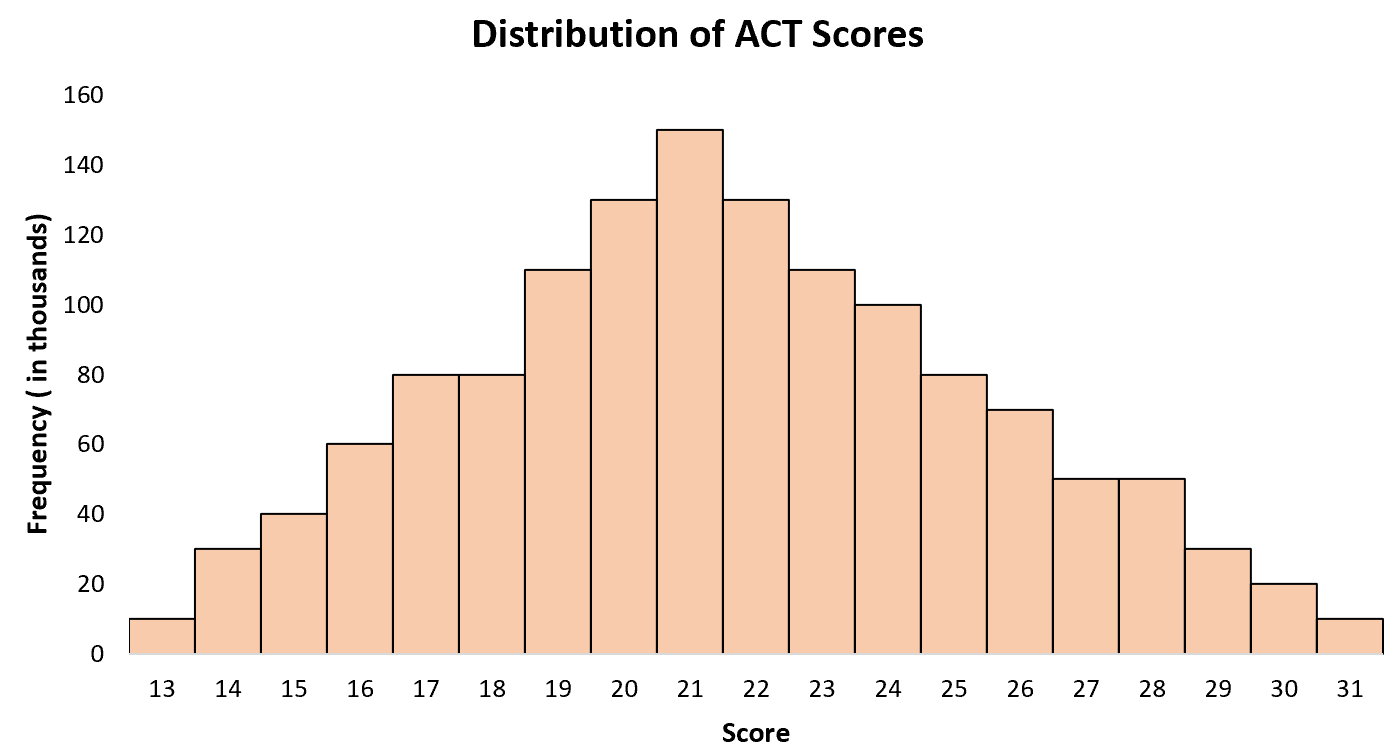
Voorbeeld 3: schoenmaten
De verdeling van herenschoenmaten is een unimodale verdeling met een ‘piek’ rond de 10. Als we een histogram maken van alle herenschoenmaten, zien we een enkele piek bij 10, waarbij sommige mannen een grotere schoenmaat dragen en anderen een grotere schoenmaat. maat. kleinere maat.
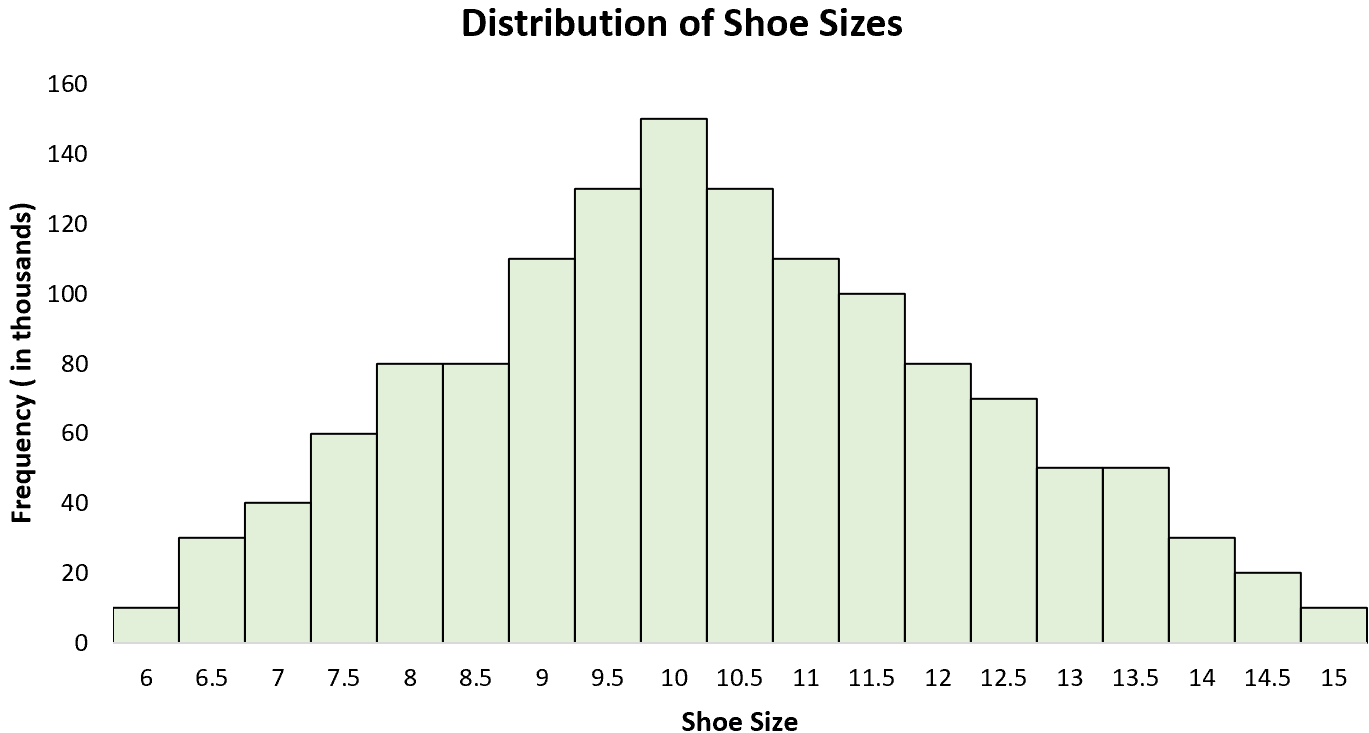
Unimodale verdelingen in statistieken
De volgende kansverdelingen in de statistieken zijn allemaal unimodale verdelingen:
De normale verdeling
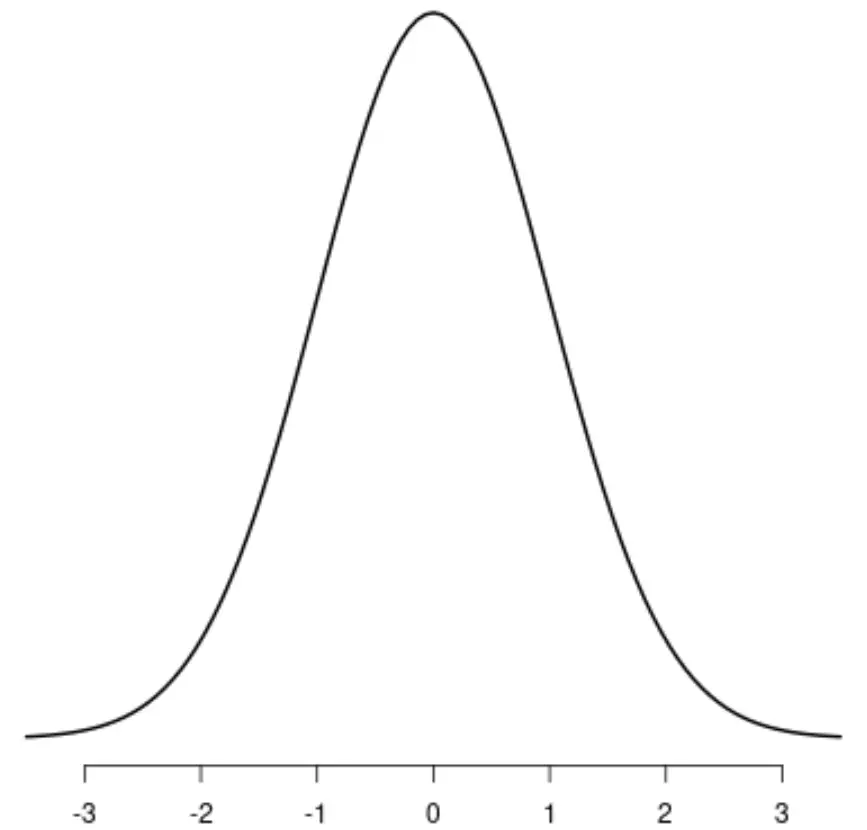
De distributie t
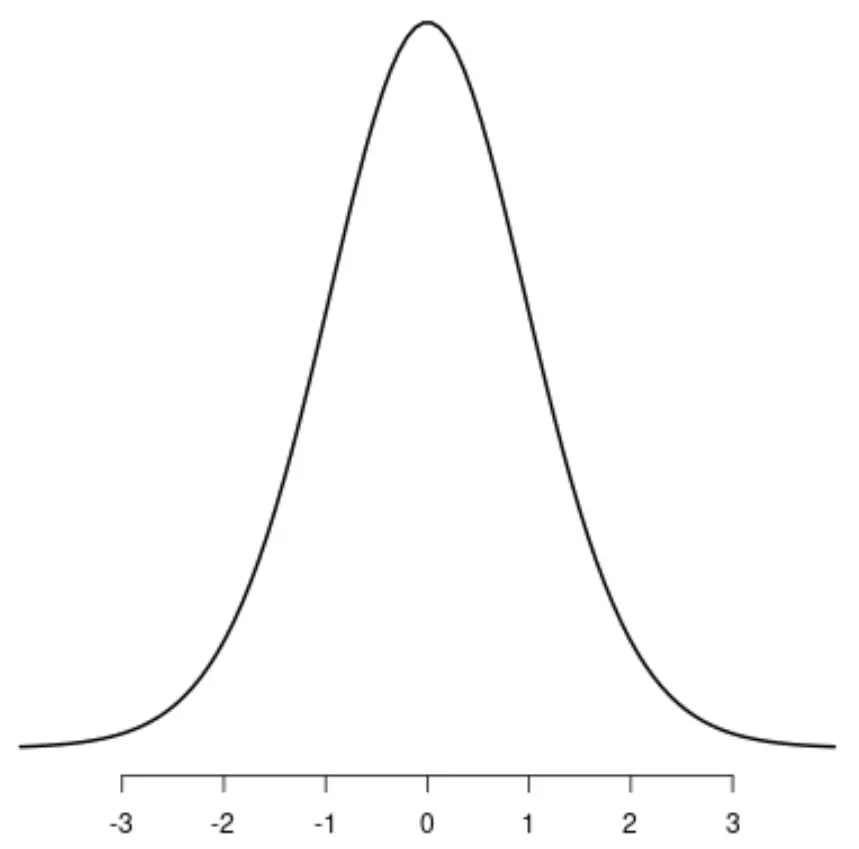
Uniforme verdeling

De Cauchy-verdeling
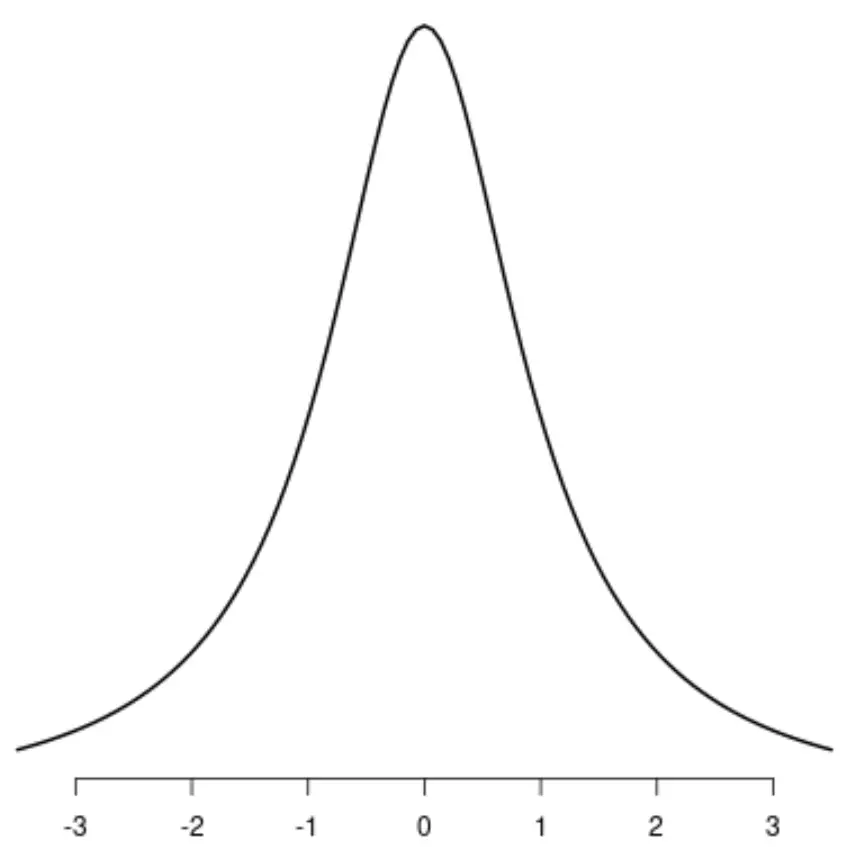
Merk op dat elk van deze verdelingen één enkele afzonderlijke piek heeft.
Hoe unimodale distributies te analyseren
We beschrijven unimodale distributies vaak met behulp van drie verschillende maten van centrale tendens :
- Gemiddelde : de gemiddelde waarde
- Mediaan : de mediaanwaarde
- Modus : de waarde die het vaakst voorkomt
Afhankelijk van deasymmetrie van de verdeling zijn deze drie metingen op verschillende plaatsen terug te vinden.
Linksscheve verdeling: gemiddelde <mediaan <modus
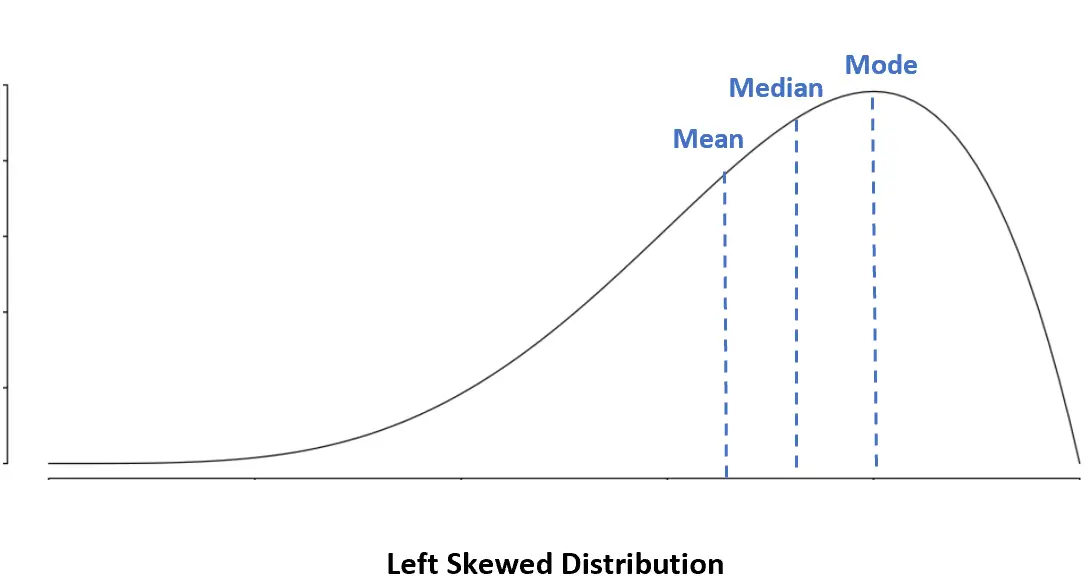
Bij een linksscheve verdeling is het gemiddelde kleiner dan de mediaan.
Rechtsscheve verdeling: Modus < Mediaan < Gemiddelde
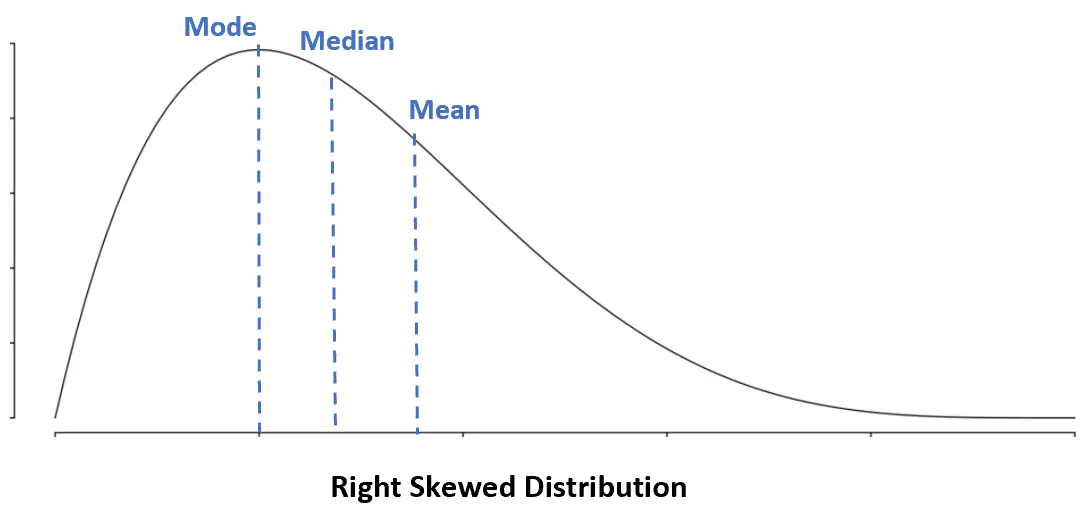
Bij een rechtsscheve verdeling is het gemiddelde groter dan de mediaan.
Geen vertekening: gemiddelde = mediaan = modus

Bij een symmetrische verdeling zijn het gemiddelde, de mediaan en de modus allemaal gelijk.
Aanvullende bronnen
Links- of rechtsscheve verdelingen
Symmetrische verdelingen: definitie + voorbeelden