Wat is een factoriële anova? (definitie & #038; voorbeeld)

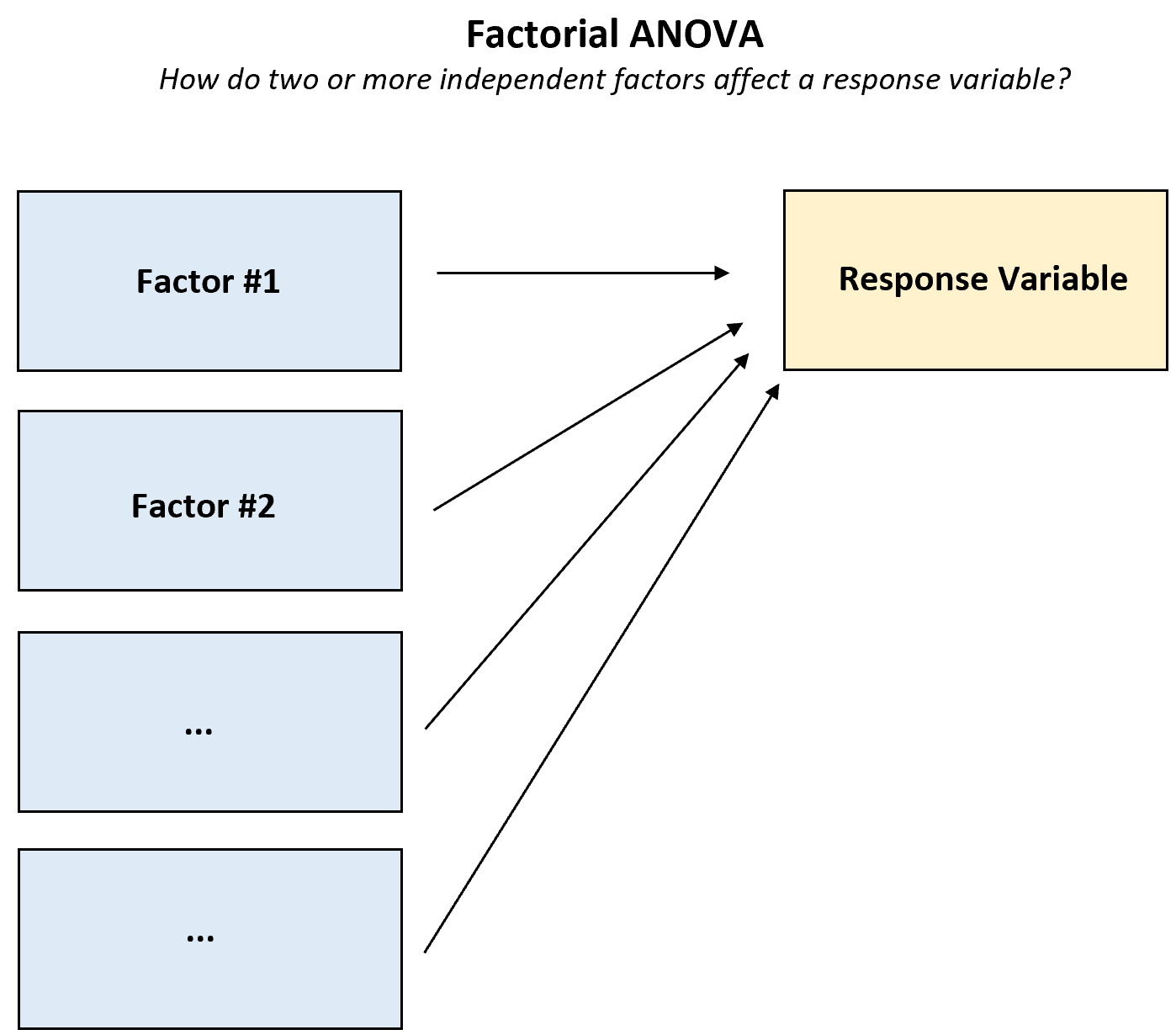
Een factoriële ANOVA is elke ANOVA (“variantieanalyse”) die twee of meer onafhankelijke factoren en één enkele responsvariabele gebruikt.

Dit type ANOVA moet worden gebruikt wanneer u wilt begrijpen hoe twee of meer factoren eenresponsvariabele beïnvloeden en of er al dan niet een interactie-effect is tussen de factoren op de responsvariabele.

Deze tutorial biedt verschillende voorbeelden van situaties waarin een factoriële ANOVA kan worden gebruikt, evenals een stapsgewijs voorbeeld van hoe u een factoriële ANOVA kunt uitvoeren.

Opmerking: een tweeweg-ANOVA is een type factoriële ANOVA.

Voorbeelden van het gebruik van een factoriële ANOVA

In elk van de volgende situaties kan een factoriële ANOVA worden gebruikt.

Voorbeeld 1: Plantengroei

Een botanicus wil begrijpen hoe blootstelling aan de zon en de waterfrequentie de plantengroei beïnvloeden. Ze plant 100 zaden en laat ze drie maanden lang groeien onder verschillende omstandigheden wat betreft blootstelling aan de zon en waterfrequentie. Na drie maanden registreert ze de hoogte van elke plant.

In dit geval heeft het de volgende variabelen:

• Responsvariabele: plantengroei
• Factoren: blootstelling aan de zon, waterfrequentie

En ze wil graag de volgende vragen beantwoorden:

• Heeft blootstelling aan de zon invloed op de plantengroei?
• Heeft de waterfrequentie invloed op de plantengroei?
• Is er een interactie-effect tussen blootstelling aan de zon en de waterfrequentie?

Ze zou voor deze analyse een factoriële ANOVA kunnen gebruiken, omdat ze wil begrijpen hoe twee factoren een enkele responsvariabele beïnvloeden.

Voorbeeld 2: Examenresultaten

Een professor wil begrijpen hoe lestijd en lesmethode de examenresultaten beïnvloeden. Het maakt gebruik van twee verschillende lesmethoden en twee verschillende lestijden (vroege ochtend en vroege middag) en registreert de gemiddelde examenscores van elke student aan het einde van het semester.

In dit geval heeft het de volgende variabelen:

• Responsvariabele: examenscore
• Factoren: lesmethode, lestijd

En hij wil graag de volgende vragen beantwoorden:

• Heeft de lesmethode invloed op de examenresultaten?
• Heeft de lestijd invloed op de examenscores?
• Is er sprake van een interactie-effect tussen lesmethode en lestijd?

Hij zou voor deze analyse een factoriële ANOVA kunnen gebruiken, omdat hij wil begrijpen hoe twee factoren een enkele responsvariabele beïnvloeden.

Voorbeeld 3: Jaarinkomen

Een econoom verzamelt gegevens om te begrijpen hoe het opleidingsniveau (middelbare schooldiploma, universiteitsdiploma, universitair diploma), burgerlijke staat (alleenstaand, gescheiden, getrouwd) en regio (Noord, Oost, Zuid, West) het jaarinkomen beïnvloeden.

In dit geval heeft het de volgende variabelen:

• Responsvariabele: jaarinkomen
• Factoren: opleidingsniveau, burgerlijke staat, regio

En hij wil graag de volgende vragen beantwoorden:

• Heeft het opleidingsniveau invloed op het inkomen?
• Heeft de burgerlijke staat invloed op het inkomen?
• Heeft de regio invloed op het inkomen?
• Is er een interactie-effect tussen deze drie onafhankelijke factoren?

Hij zou voor deze analyse een factoriële ANOVA kunnen gebruiken, omdat hij wil begrijpen hoe drie factoren een enkele responsvariabele beïnvloeden.

Stapsgewijs voorbeeld van een factoriële ANOVA

Een botanicus wil weten of blootstelling aan zonlicht en de frequentie van water geven de plantengroei beïnvloeden. Ze plant 40 zaden en laat ze twee maanden lang groeien onder verschillende omstandigheden wat betreft blootstelling aan de zon en waterfrequentie. Na twee maanden registreert ze de hoogte van elke plant.

De resultaten worden hieronder weergegeven:

We kunnen zien dat er onder elke combinatie van omstandigheden vijf planten werden gekweekt.

Er werden bijvoorbeeld vijf planten gekweekt met dagelijks water en zonder zonlicht en hun hoogten na twee maanden waren 4,8 inch, 4,4 inch, 3,2 inch, 3,9 inch en 4,4 inch:

De botanicus gebruikt deze gegevens om een factoriële ANOVA uit te voeren in Excel en krijgt het volgende resultaat:

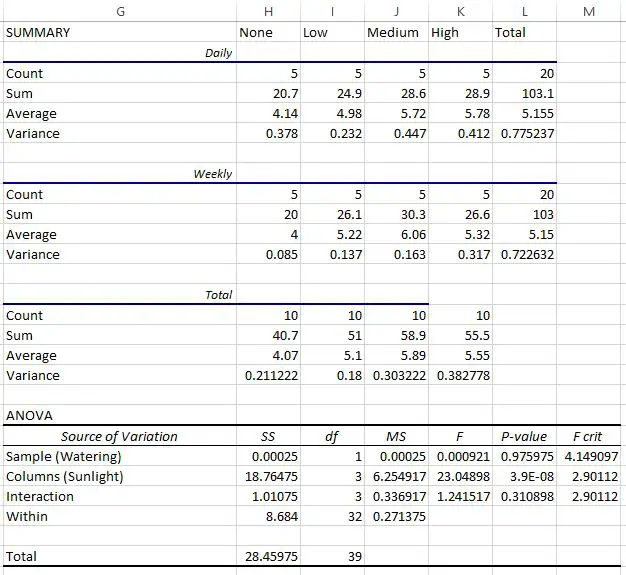
De laatste tabel toont het resultaat van de factoriële ANOVA:

• De p-waarde voor de interactie tussen de waterfrequentie en de blootstelling aan de zon was 0,310898 . Dit is niet statistisch significant op het alfaniveau van 0,05.
• De p-waarde voor de bewateringsfrequentie was 0,975975 . Dit is niet statistisch significant op het alfaniveau van 0,05.
• De p-waarde voor blootstelling aan de zon was 3,9E-8 (0,000000039) . Dit is statistisch significant op het alfaniveau van 0,05.

We kunnen concluderen dat blootstelling aan zonlicht de enige factor is met een statistisch significant effect op de plantengroei.

We kunnen ook concluderen dat er geen interactie-effect is tussen blootstelling aan de zon en de waterfrequentie en dat de waterfrequentie geen statistisch significant effect heeft op de plantengroei. planten.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over ANOVA-modellen:

Een inleiding tot One-Way ANOVA
Een inleiding tot tweerichtings-ANOVA
Een inleiding tot ANOVA met herhaalde metingen
De verschillen tussen ANOVA, ANCOVA, MANOVA en MANCOVA