Aangepaste oddsratio: definitie + voorbeelden

In de statistieken vertelt een odds ratio ons de verhouding tussen de waarschijnlijkheid dat een gebeurtenis optreedt in een behandelgroep en de waarschijnlijkheid dat een gebeurtenis optreedt in een controlegroep.

Odds ratio’s komen het meest voor in logistische regressie , een methode die we gebruiken om een regressiemodel te fitten dat een of meer voorspellende variabelen en een binaire responsvariabele heeft.

Een aangepaste oddsratio is een oddsratio die is aangepast voor andere voorspellende variabelen in een model.

Het is vooral nuttig om ons te helpen begrijpen hoe een voorspellende variabele de kans beïnvloedt dat een gebeurtenis plaatsvindt, na aanpassing voor het effect van andere voorspellende variabelen.

Het volgende voorbeeld illustreert het verschil tussen een odds ratio en een aangepaste odds ratio.

Voorbeeld: Berekening van aangepaste oddsratio’s

Stel dat we willen begrijpen of de leeftijd van een moeder invloed heeft op de kans op een baby met een laag geboortegewicht.

Om dit te onderzoeken kunnen we logistische regressie uitvoeren met leeftijd als voorspellende variabele en een laag geboortegewicht (ja of nee) alsresponsvariabele .

Stel dat we gegevens verzamelen over 300 moeders en passen in een logistisch regressiemodel. Hier zijn de resultaten:

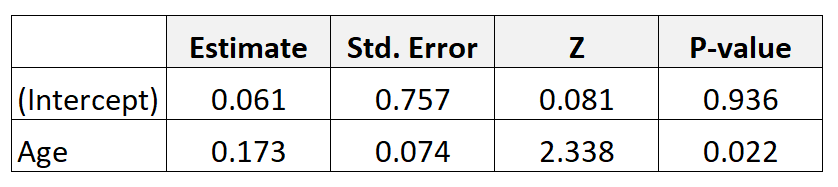
Om de oddsratio voor leeftijd te verkrijgen, kunt u eenvoudigweg de coëfficiëntschatting uit de tabel exponentiëren: e ^0,173 = 1,189 .

Dit vertelt ons dat een leeftijdstoename van één jaar gepaard gaat met een toename van 1.189 in de kans dat een baby een laag geboortegewicht heeft. Met andere woorden: de kans op het krijgen van een baby met een laag geboortegewicht neemt met 18,9% toe voor elke extra jaarlijkse leeftijdstoename.

Deze odds ratio wordt de „ruwe“ odds ratio of „niet-aangepaste“ odds ratio genoemd, omdat deze niet is aangepast voor de andere voorspellende variabelen in het model, aangezien het de enige voorspellende variabele in het model is.

Maar stel dat we willen begrijpen of de leeftijd en het rookgedrag van een moeder invloed hebben op de kans op een baby met een laag geboortegewicht.

Om dit te onderzoeken kunnen we logistische regressie uitvoeren met leeftijd en roken (ja of nee) als voorspellende variabelen en een laag geboortegewicht alsresponsvariabele .

Stel dat we gegevens verzamelen over 300 moeders en passen in een logistisch regressiemodel. Hier zijn de resultaten:

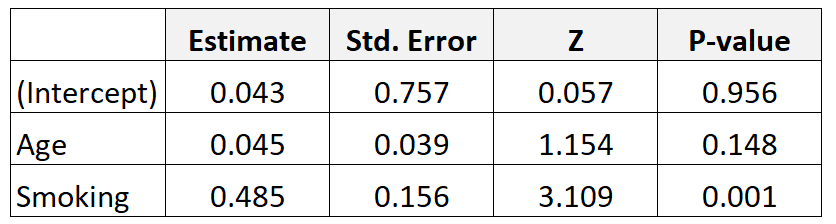
Zo interpreteert u de resultaten:

Leeftijd: De voor leeftijd gecorrigeerde odds ratio wordt als volgt berekend: e ^0,045 = 1,046 . Dit betekent dat de kans op het krijgen van een baby met een laag geboortegewicht met 4,6% toeneemt voor elke extra jaarlijkse leeftijdstoename, ervan uitgaande dat de variabele roken constant blijft.

Stel bijvoorbeeld dat moeder A en moeder B allebei roken. Als moeder A één jaar ouder is dan moeder B, dan is de kans dat moeder A een baby met een laag geboortegewicht krijgt 1,046 maal de kans dat moeder B een baby met een laag geboortegewicht krijgt.

Roken : De aangepaste oddsratio voor roken wordt als volgt berekend: ^e.485 = 1.624 . Dit betekent dat de kans op het krijgen van een baby met een laag geboortegewicht met 62,4% toeneemt als de moeder rookt (vergeleken met niet roken), ervan uitgaande dat de leeftijdsvariabele constant blijft.

Stel bijvoorbeeld dat moeder A en moeder B allebei 30 jaar oud zijn. Als moeder A rookt tijdens de zwangerschap en moeder B niet, dan is de kans dat moeder A een baby met een laag geboortegewicht krijgt 62,4% groter dan de kans dat moeder B een baby met een laag geboortegewicht krijgt.

Merk op dat de voor leeftijd gecorrigeerde odds ratio lager is dan de niet-gecorrigeerde odds ratio uit het vorige voorbeeld. Dit komt omdat wanneer andere voorspellende variabelen de kans vergroten dat de responsvariabele optreedt, de aangepaste oddsratio voor een voorspellende variabele die al in het model aanwezig is, altijd zal afnemen.

Samenvatting: oddsratio versus aangepaste oddsratio

Een oddsratio (ook wel een ‘ruwe’ oddsratio genoemd) is nuttig om ons te vertellen hoe veranderingen in een voorspellende variabele de kans beïnvloeden dat een responsvariabele optreedt.

Een aangepaste oddsratio is nuttig om ons te vertellen hoe veranderingen in een voorspellende variabele de kans beïnvloeden dat een responsvariabele optreedt, na controle voor andere voorspellende variabelen in een model.

Aanvullende bronnen

Inleiding tot logistieke regressie
Hoe logistische regressie uit te voeren in R
Hoe logistieke regressie uit te voeren in Python