Relatieve frequentie

In dit artikel leer je wat relatieve frequentie is in statistieken, hoe je relatieve frequentie kunt krijgen en twee stapsgewijze oefeningen over relatieve frequentie.

Wat is relatieve frequentie?

In de statistiek is de relatieve frequentie een maatstaf die het aantal keren aangeeft dat een waarde in een gegevensmonster voorkomt als proportie of percentage. Nauwkeuriger gezegd, de relatieve frequentie is gelijk aan de absolute frequentie gedeeld door het totale aantal gegevens.

Als de absolute frequentie van een waarde bijvoorbeeld 15 is en er in totaal 100 gegevenspunten zijn, is de relatieve frequentie van die waarde 0,15 (15/100=0,15).

Over het algemeen wordt het symbool _hi gebruikt om de relatieve frequentie weer te geven. Hoewel er nog steeds geen consensus bestaat in de statistische gemeenschap, kun je de relatieve frequentie zien die wordt weergegeven door een ander symbool.

Hoe de relatieve frequentie te berekenen

De relatieve frequentie is gelijk aan de absolute frequentie gedeeld door het totale aantal gegevens. Om de relatieve frequentie te berekenen, moet u daarom eerst de absolute frequentie vinden en deze vervolgens delen door het totale aantal waarnemingen.

De formule voor de relatieve frequentie is dus als volgt:

Goud:

• 

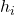
  is de relatieve frequentie.

• 

  is de absolute frequentie.

• 

  is het totale aantal gegevens.

Aan de andere kant, om de relatieve frequentie in procenten te berekenen, dat wil zeggen de relatieve frequentie uitgedrukt als percentage, vermenigvuldigt u eenvoudigweg de vorige formule met 100:

Voorbeelden van relatieve frequentie

Nadat u de definitie van relatieve frequentie heeft gezien, vindt u hieronder twee voorbeelden uit de praktijk, zodat u kunt zien hoe dit type frequentie wordt berekend. In het eerste voorbeeld wordt de relatieve frequentie van een discrete variabele bepaald en in het tweede voorbeeld van een continue variabele.

Voorbeeld 1: discrete variabele

• De cijfers behaald voor het vak statistiek in een klas van 30 studenten zijn als volgt. Wat is de relatieve frequentie van elke noot?

De variabele in deze oefening is discreet omdat de gegevens alleen gehele getallen kunnen zijn; daarom is het niet nodig om de gegevens in intervallen te groeperen.

Om de relatieve frequentie te vinden, moeten we eerst de absolute frequentie bepalen. We construeren dus een frequentietabel en berekenen de absolute frequentie voor elke verschillende waarde:

Nu we de absolute frequentie hebben berekend, kunnen we de relatieve frequentie berekenen. Om dit te doen, deelt u eenvoudigweg elke absolute frequentie door het totale aantal gegevens (30):

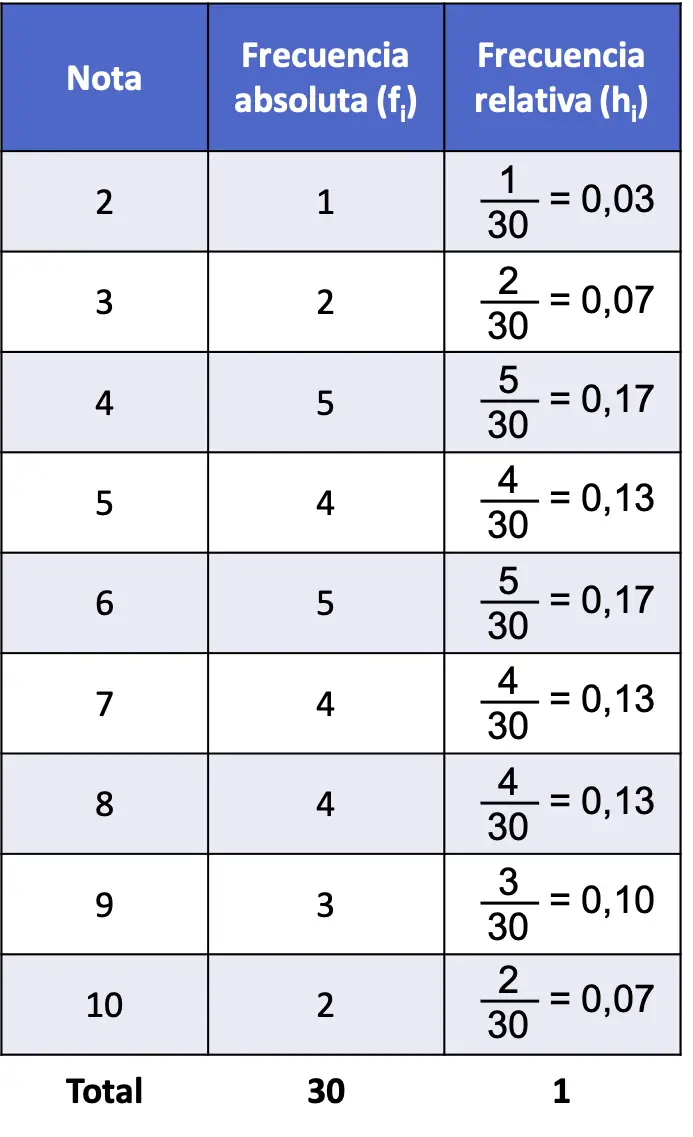
De frequentietabel van het probleem met absolute frequentie en relatieve frequentie is dus als volgt:

Merk op dat de som van alle relatieve frequenties altijd 1 oplevert, anders betekent dit dat sommige berekeningen verkeerd zijn.

Voorbeeld 2: continue variabele

• De lengte van 20 personen werd gemeten en de onderstaande resultaten werden verkregen. Verdeel de gegevens in intervallen en vind de relatieve frequentie van elk interval.

De gegevens in dit statistische voorbeeld behoren tot een continue variabele, aangezien ze decimaal zijn en de variabele daarom elke waarde kan aannemen. Dus voordat we de frequentieberekeningen uitvoeren, zullen we de gegevens eerst groeperen in intervallen met een amplitude van 10 tienden.

Vervolgens maken we een frequentietabel met de absolute frequentie van elk interval:

En zodra we de absolute frequentie hebben gevonden, kunnen we de relatieve frequentie van elk interval bepalen door de absolute frequentie ervan te delen door het totale aantal gegevens (20):

Cumulatieve relatieve frequentie

Zoals de naam al doet vermoeden, is cumulatieve relatieve frequentie een ander type frequentie dat in statistieken wordt gebruikt en wordt berekend op basis van de relatieve frequentie.

Nauwkeuriger gezegd: de cumulatieve relatieve frequentie van een waarde is gelijk aan de som van de relatieve frequentie van de waarde zelf plus de relatieve frequenties van alle kleinere waarden.

Om u te laten zien hoe de cumulatieve relatieve frequentie wordt verkregen, is hieronder de cumulatieve relatieve frequentie van de dataset in het eerste voorbeeld berekend: