Anova versus regressie: wat is het verschil?
Twee veelgebruikte modellen in de statistiek zijn ANOVA- en regressiemodellen.
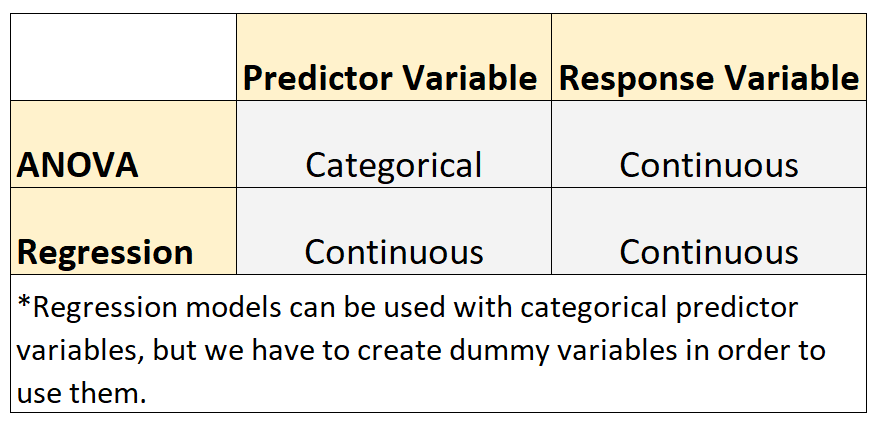
Deze twee soorten modellen delen de volgende gelijkenis:
- Deresponsvariabele in elk model is continu. Voorbeelden van continue variabelen zijn gewicht, lengte, lengte, breedte, tijd, leeftijd, enz.
Deze twee soorten modellen hebben echter het volgende verschil :
- ANOVA-modellen worden gebruikt wanneer de voorspellende variabelen categorisch zijn. Voorbeelden van categorische variabelen zijn opleidingsniveau, oogkleur, burgerlijke staat, enz.
- Regressiemodellen worden gebruikt als de voorspellende variabelen continu zijn.*
*Regressiemodellen kunnen worden gebruikt met categorische voorspellende variabelen, maar we moeten dummyvariabelen maken om ze te gebruiken.
De volgende voorbeelden laten zien wanneer u ANOVA- of regressiemodellen in de praktijk kunt gebruiken.
Voorbeeld 1: Voorkeurs-ANOVA-model
Stel dat een bioloog wil begrijpen of vier verschillende meststoffen over een periode van een maand tot dezelfde gemiddelde plantengroei (in inches) leiden. Om dit te testen, brengt ze elke meststof aan op twintig planten en registreert ze na een maand de groei van elke plant.
In dit scenario moet de bioloog een eenrichtings-ANOVA-model gebruiken om de verschillen tussen meststoffen te analyseren, omdat er een voorspellende variabele is en deze categorisch is.
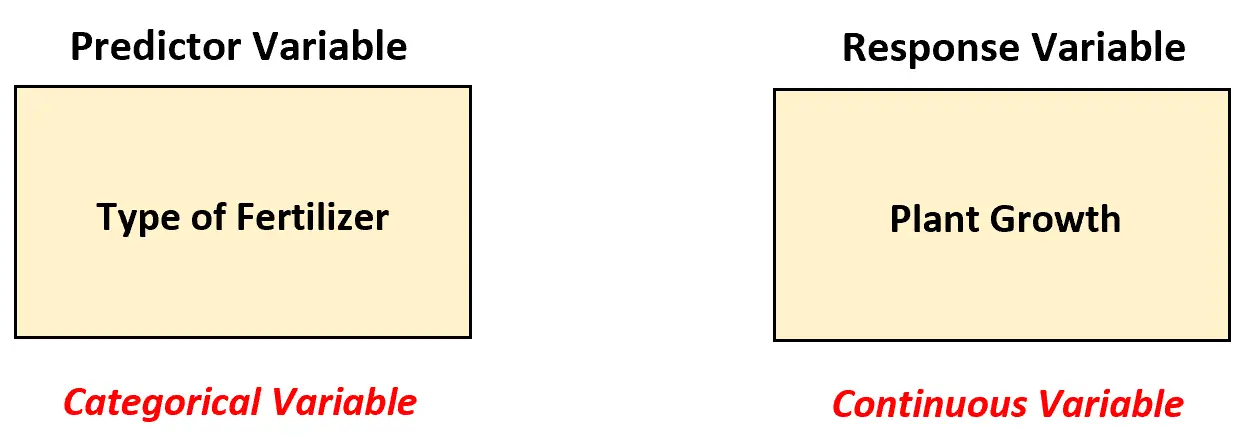
Met andere woorden, de waarden van de voorspellende variabele kunnen in de volgende “categorieën” worden ingedeeld:
- Meststof 1
- Meststof 2
- Meststof 3
- Meststof 4
Een one-way ANOVA zal de bioloog vertellen of de gemiddelde plantengroei gelijk is tussen de vier verschillende meststoffen.
Voorbeeld 2: Voorkeursregressiemodel
Laten we zeggen dat een makelaar de relatie tussen vierkante meters en de prijs van onroerend goed wil begrijpen. Om deze relatie te analyseren, verzamelt hij gegevens over de vierkante meters en de prijs van 200 woningen in een bepaalde stad.
In dit scenario moet de makelaar een eenvoudig lineair regressiemodel gebruiken om de relatie tussen deze twee variabelen te analyseren, omdat de voorspellende variabele (vierkante meters) continu is.
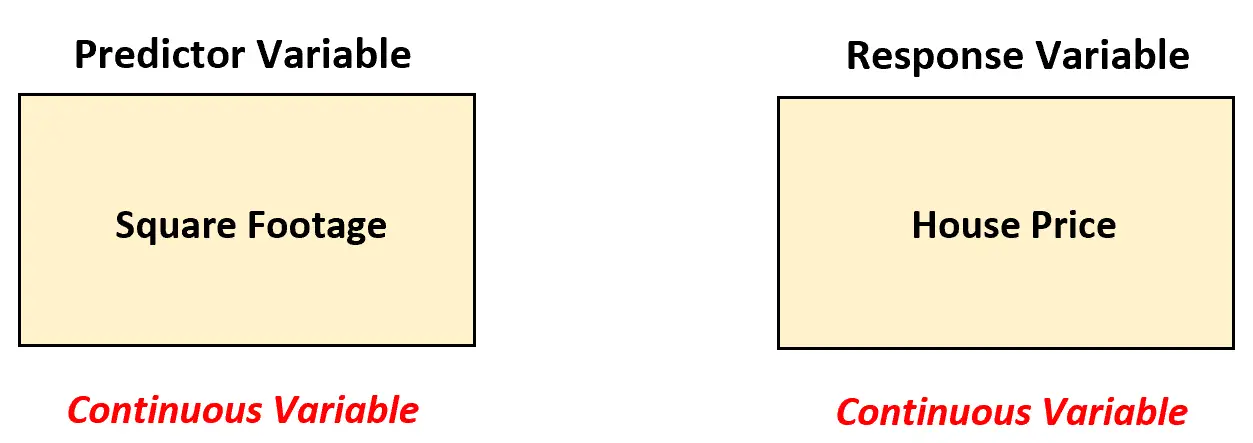
Met behulp van eenvoudige lineaire regressie kan de makelaar in het volgende regressiemodel passen:
Vastgoedprijs = β 0 + β 1 (vierkante oppervlakte)
De waarde van β 1 vertegenwoordigt de gemiddelde verandering in de huizenprijs die gepaard gaat met elke extra vierkante meter.
Hierdoor kan de makelaar de relatie tussen vierkante meters en de vastgoedprijs kwantificeren.
Voorbeeld 3: Regressiemodel met voorkeursdummyvariabelen
Stel dat een makelaar de relatie wil begrijpen tussen de voorspellende variabelen “vierkante meters” en “woningtype” (eengezinswoning, appartement, herenhuis) met de responsvariabele van de vastgoedprijs.
In dit scenario kan de makelaar meerdere lineaire regressies gebruiken door ‚woningtype‘ om te zetten in een dummyvariabele, aangezien dit momenteel een categorische variabele is.
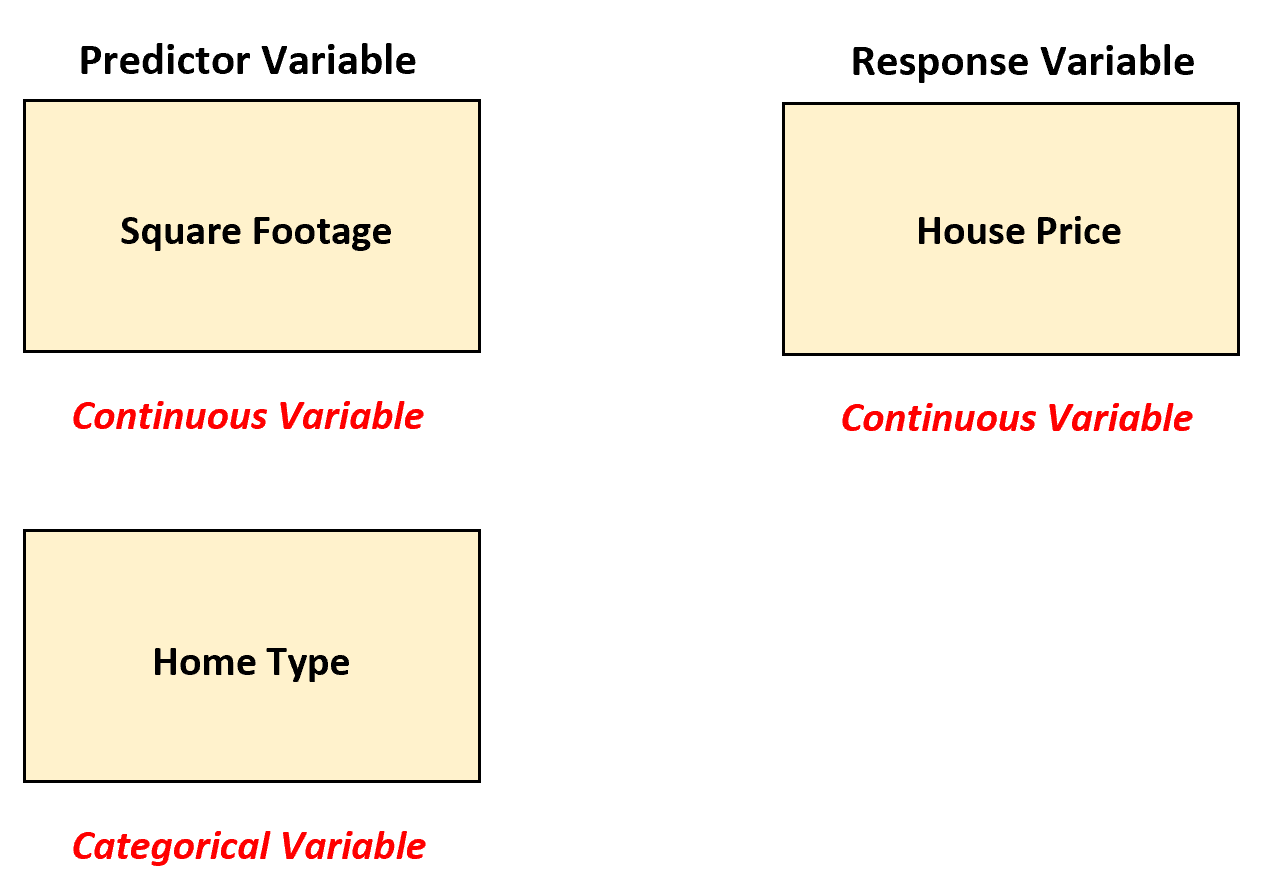
De makelaar in onroerend goed kan dan voldoen aan het volgende meervoudige lineaire regressiemodel:
Vastgoedprijs = β 0 + β 1 (vierkante oppervlakte) + β 2 (eengezinswoning) + β 3 (appartement)
Hier ziet u hoe we de modelcoëfficiënten zouden interpreteren:
- β 1 : De gemiddelde verandering in de huizenprijs geassocieerd met één vierkante meter extra.
- β 2 : Het gemiddelde prijsverschil tussen een eengezinswoning en een herenhuis, ervan uitgaande dat het aantal vierkante meters constant blijft.
- β 3 : Gemiddeld prijsverschil tussen een eengezinswoning en een appartement, uitgaande van een constante oppervlakte.
Bekijk de volgende tutorials om te zien hoe u dummyvariabelen maakt in verschillende statistische software:
Aanvullende bronnen
De volgende tutorials bieden een diepgaande introductie tot ANOVA-modellen:
De volgende tutorials bieden een diepgaande introductie tot lineaire regressiemodellen: