Waarom zijn statistieken belangrijk? (10 redenen waarom statistieken belangrijk zijn!)

Het vakgebied statistiek houdt zich bezig met het verzamelen, analyseren, interpreteren en presenteren van gegevens.

Naarmate technologie steeds meer aanwezig wordt in ons dagelijks leven, worden er meer gegevens gegenereerd en verzameld dan ooit tevoren in de menselijke geschiedenis.

Statistiek is het gebied dat ons kan helpen begrijpen hoe we deze gegevens kunnen gebruiken om de volgende taken uit te voeren:

• De wereld om ons heen beter begrijpen.
• Neem beslissingen met behulp van data.
• Maak voorspellingen over de toekomst met behulp van data.

In dit artikel delen we 10 redenen waarom het vakgebied statistiek zo belangrijk is in het moderne leven.

Reden 1: Gebruik beschrijvende statistieken om de wereld te begrijpen

Beschrijvende statistiek wordt gebruikt om een stukje ruwe data te beschrijven. Er zijn drie hoofdtypen beschrijvende statistieken:

• Samenvattende statistieken
• Grafisch
• de tafels

Elk van deze elementen kan ons helpen bestaande gegevens beter te begrijpen.

Laten we bijvoorbeeld zeggen dat we een ruwe dataset hebben die de testscores van 10.000 studenten in een bepaalde stad laat zien. We kunnen beschrijvende statistieken gebruiken om:

• Bereken de gemiddelde testscore en de standaardafwijking van de testresultaten.
• Genereer een histogram of boxplot om de verdeling van de testresultaten te visualiseren.
• Maak een frequentietabel om de verdeling van testresultaten te begrijpen.

Door beschrijvende statistieken te gebruiken, kunnen we de toetsscores van studenten veel gemakkelijker begrijpen dan alleen door naar de onbewerkte gegevens te kijken.

Reden 2: Pas op voor misleidende afbeeldingen

Er worden steeds meer afbeeldingen gegenereerd in tijdschriften, media, online artikelen en tijdschriften. Helaas kunnen grafieken vaak misleidend zijn als u de onderliggende gegevens niet begrijpt.

Stel bijvoorbeeld dat een tijdschrift een onderzoek publiceert waarin een negatieve correlatie wordt gevonden tussen de GPA- en ACT-scores van studenten aan een bepaalde universiteit.

Deze negatieve correlatie treedt echter alleen op omdat studenten met zowel een hoge GPA- als een ACT-score naar een elite-universiteit kunnen gaan, terwijl studenten met zowel een lage GPA- als een ACT-score helemaal niet worden toegelaten.

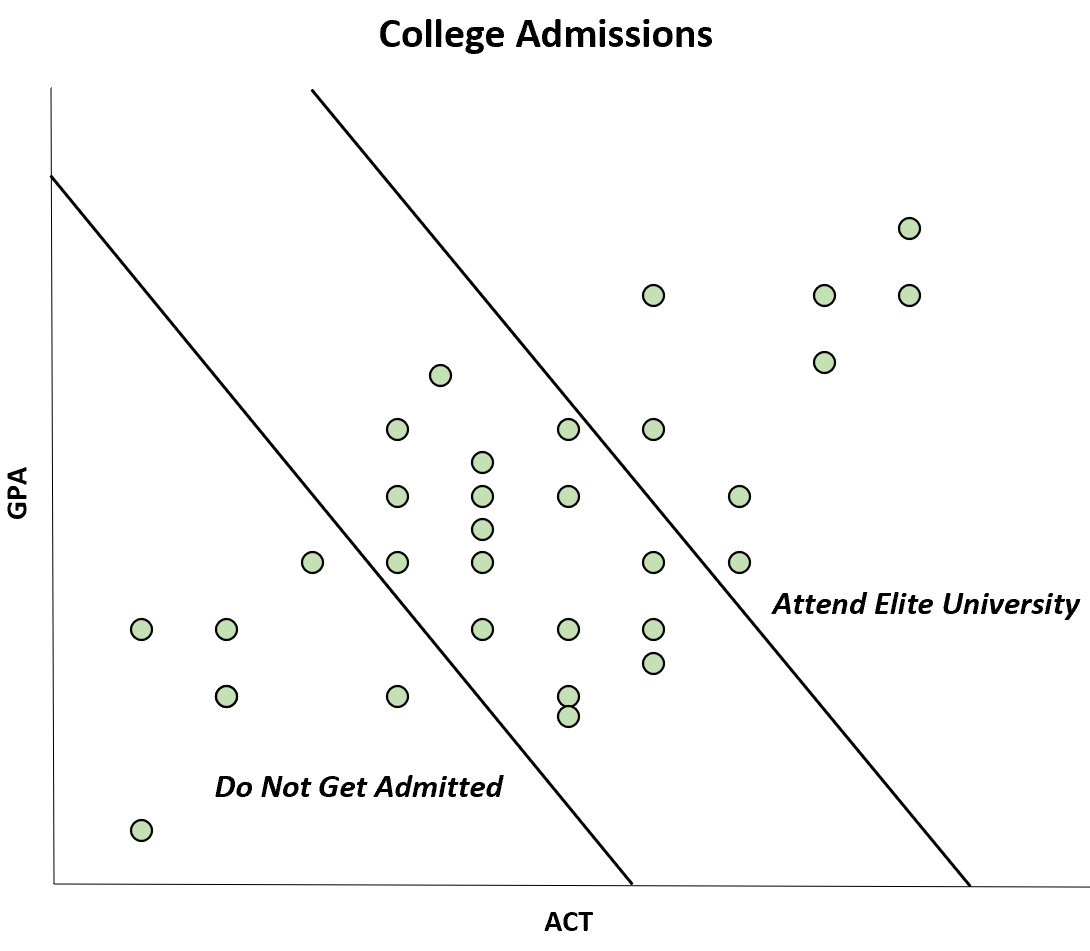
Hoewel de correlatie tussen ACT en GPA positief is in de populatie, lijkt de correlatie negatief in de steekproef.

Deze specifieke bias staat bekend als de Berkson bias . Door u bewust te zijn van deze vooringenomenheid, kunt u voorkomen dat u door bepaalde grafieken wordt misleid.

Reden 3: wees op uw hoede voor verwarrende variabelen

Een belangrijk concept dat u in de statistiek zult leren, is het concept van verwarrende variabelen .

Dit zijn variabelen waarmee geen rekening wordt gehouden en die de resultaten van een experiment kunnen verwarren en tot onbetrouwbare conclusies kunnen leiden.

Stel bijvoorbeeld dat een onderzoeker gegevens verzamelt over de verkoop van ijs en aanvallen van haaien en ontdekt dat de twee variabelen sterk gecorreleerd zijn. Betekent dit dat de toegenomen verkoop van ijs meer haaienaanvallen veroorzaakt?

Het is onwaarschijnlijk. De meest waarschijnlijke oorzaak is de verwarrende variabele temperatuur . Als het buiten warmer is, kopen meer mensen ijs en gaan meer mensen naar de oceaan.

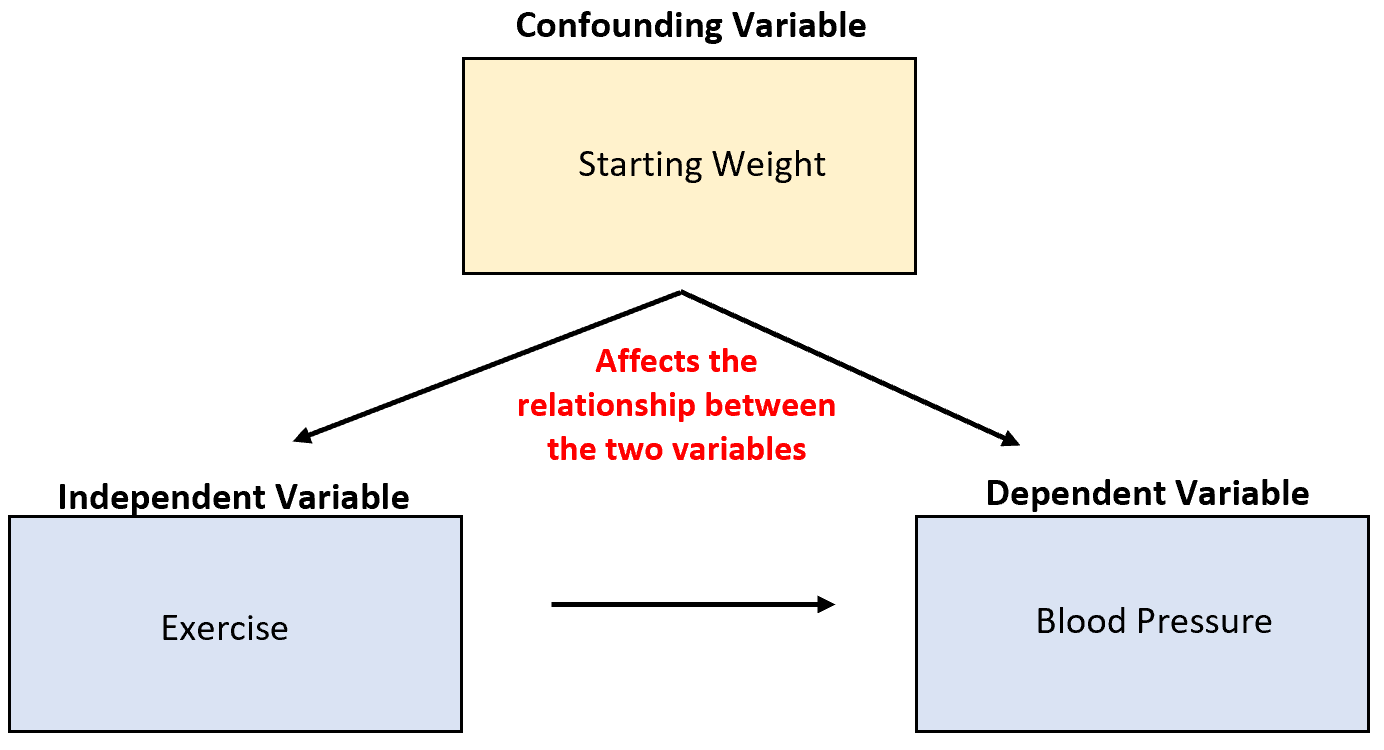
Reden 4: betere beslissingen nemen met behulp van waarschijnlijkheden

Een van de belangrijkste deelgebieden van de statistiek is waarschijnlijkheid . Het is het veld dat de waarschijnlijkheid bestudeert dat gebeurtenissen plaatsvinden.

Door een basiskennis van waarschijnlijkheid te hebben, kunt u beter geïnformeerde beslissingen nemen in de echte wereld.

Stel bijvoorbeeld dat een middelbare scholier weet dat hij 10% kans heeft om toegelaten te worden tot een bepaalde universiteit. Met behulp van de formule voor de kans om „ten minste één“ te behalen , kan deze student de waarschijnlijkheid berekenen dat hij wordt toegelaten tot ten minste één universiteit waarvoor hij solliciteert en kan hij het aantal universiteiten waarvoor hij solliciteert op basis van het resultaat aanpassen.

Reden 5: P-waarden in onderzoek begrijpen

Een ander belangrijk concept waarover u in de statistiek zult leren, zijn p-waarden .

De klassieke definitie van een p-waarde is:

Een p-waarde is de waarschijnlijkheid dat u een steekproefstatistiek waarneemt die minstens zo extreem is als uw steekproefstatistiek, gegeven het feit dat de nulhypothese waar is.

Stel bijvoorbeeld dat een fabriek beweert banden te produceren met een gemiddeld gewicht van 200 pond. Een auditor veronderstelt dat het werkelijke gemiddelde gewicht van de in deze fabriek geproduceerde banden 200 pond afwijkt. Hij voert dus een hypothesetest uit en ontdekt dat de p-waarde van de test 0,04 is.

Zo interpreteert u deze p-waarde:

Als de fabriek daadwerkelijk banden produceert met een gemiddeld gewicht van 200 pond, zal 4% van alle audits het in de steekproef waargenomen effect bereiken, of meer, als gevolg van willekeurige steekproeffouten. Dit vertelt ons dat het verkrijgen van de door de auditor verkregen voorbeeldgegevens vrij zeldzaam zou zijn als de fabriek daadwerkelijk banden zou produceren met een gemiddeld gewicht van 200 pond.

De auditor zou dus waarschijnlijk de nulhypothese verwerpen dat het werkelijke gemiddelde gewicht van de in deze fabriek geproduceerde banden inderdaad 200 pond bedraagt.

Reden 6: Begrijp de correlatie

Een ander belangrijk concept dat je in de statistiek leert, iscorrelatie , wat ons de lineaire associatie tussen twee variabelen vertelt.

De waarde van een correlatiecoëfficiënt ligt altijd tussen -1 en 1 waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

Door deze waarden te begrijpen, kunt u de relatie tussen variabelen in de echte wereld begrijpen.

Als de correlatie tussen advertentie-uitgaven en inkomsten bijvoorbeeld 0,87 is, kun je begrijpen dat er een sterk positief verband bestaat tussen de twee variabelen. Naarmate u meer geld uitgeeft aan advertenties, kunt u een voorspelbare omzetstijging verwachten.

Reden 7: Maak voorspellingen over de toekomst

Een andere belangrijke reden om statistieken te leren is het begrijpen van fundamentele regressiemodellen zoals:

• Eenvoudige lineaire regressie
• Meerdere lineaire regressie
• Logistieke regressie

Met elk van deze modellen kunt u voorspellingen doen over de toekomstige waarde van eenresponsvariabele op basis van de waarde van bepaalde voorspellende variabelen in het model.

Bedrijven gebruiken bijvoorbeeld voortdurend meerdere lineaire regressiemodellen in de echte wereld bij het gebruik van voorspellende variabelen zoals leeftijd, inkomen, etniciteit, enz. om te voorspellen hoeveel klanten in hun winkels zullen uitgeven.

Op dezelfde manier gebruiken logistieke bedrijven voorspellende variabelen zoals de totale vraag, de bevolkingsomvang, enz. om toekomstige verkopen te voorspellen.

In welk vakgebied je ook werkt, de kans is groot dat regressiemodellen worden gebruikt om een toekomstig fenomeen te voorspellen.

Reden 8: Begrijp mogelijke vooroordelen in onderzoeken

Een andere reden om statistieken te bestuderen is om je bewust te zijn van alle verschillende soorten vooroordelen die kunnen optreden in praktijkstudies.

Hier zijn enkele voorbeelden:

• Observeer vooroordelen
• Vooroordeel over zelfselectie
• Referentie bias
• Weggelaten variabele bias
• Onderschattingsvooroordeel
• Non-respons bias

Door een basiskennis te hebben van dit soort vooroordelen, kunt u voorkomen dat u zich hieraan schuldig maakt bij het uitvoeren van onderzoek, of kunt u zich ervan bewust zijn wanneer u andere onderzoeksartikelen of onderzoeken leest.

Reden 9: Begrijp de aannames van statistische tests

Veel statistische tests maken aannames over de onderliggende gegevens die worden bestudeerd.

Wanneer u de resultaten van een onderzoek leest of zelfs uw eigen onderzoek uitvoert, is het belangrijk om te begrijpen welke aannames moeten worden gedaan om de resultaten betrouwbaar te maken.

De volgende artikelen delen de aannames die zijn gemaakt in veelgebruikte statistische tests en procedures:

• Wat is de aanname van gelijke variantie in de statistiek?
• Wat is de normaliteitsaanname in de statistiek?
• Wat is de onafhankelijkheidsaanname in de statistiek?

Reden 10: Om overgeneralisatie te voorkomen

Een andere reden om statistieken te bestuderen is om het concept van overgeneralisatie te begrijpen.

Dit gebeurt wanneer de individuen die aan een onderzoek deelnemen niet representatief zijn voor individuen in de totale populatie en het daarom ongepast is om de bevindingen van een onderzoek te generaliseren naar de hele populatie.

Laten we bijvoorbeeld zeggen dat we willen weten welk percentage van de leerlingen op een bepaalde school de voorkeur geeft aan ‚drama‘ als hun favoriete filmgenre. Als de totale studentenpopulatie uit een mix van 50% jongens en 50% meisjes bestaat, zou een steekproef bestaande uit 90% jongens en 10% meisjes tot vertekende resultaten kunnen leiden als aanzienlijk minder jongens theater als favoriet genre verkiezen.

Idealiter willen we dat onze steekproef lijkt op een ‘miniversie’ van onze populatie. Als de totale studentenpopulatie dus voor 50% uit meisjes en voor 50% uit jongens bestaat, zou onze steekproef niet representatief zijn als deze voor 90% uit jongens en slechts 10% uit meisjes zou bestaan.

Dus of u nu uw eigen enquête uitvoert of de resultaten van een enquête leest, het is belangrijk om te begrijpen of de steekproefgegevens representatief zijn voor de totale populatie en of de enquêteresultaten met vertrouwen kunnen worden gegeneraliseerd naar de populatie.

Aanvullende bronnen

Bekijk de volgende artikelen om basiskennis te krijgen van de belangrijkste concepten in inleidende statistieken:

Beschrijvende of inferentiële statistieken
Bevolking versus steekproef
Statistieken versus parameters
Kwalitatieve en kwantitatieve variabelen
Meetniveaus: nominaal, ordinaal, interval en ratio