Hoe u het midden en de spreiding van een puntendiagram kunt vinden
Een puntplot is een soort plot dat de frequenties van waarden in een dataset weergeeft met behulp van gestapelde punten.
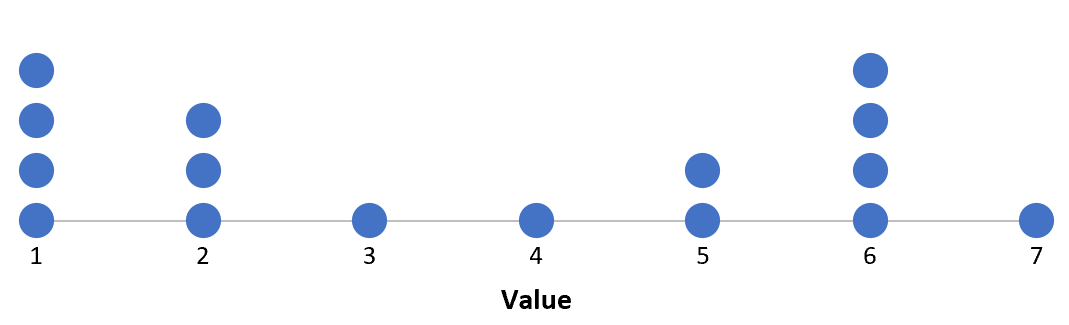
Als we een puntendiagram maken, willen we vaak het centrum en de distributie kwantificeren:
- Midden : het centrale punt van de gegevensset. Om dit te meten gebruiken we vaak de mediaan.
- Spreiding : de verdeling van waarden in de dataset. Om dit te meten gebruiken we vaak bereik.
Door alleen deze twee waarden te kennen, kunnen we een goed beeld krijgen van hoe de waarden verdeeld zijn in een bepaalde dataset.
De volgende voorbeelden laten zien hoe u in de praktijk het middelpunt en de omvang van een puntendiagram kunt vinden.
Voorbeeld 1: Puntdiagram van gemaakte fouten
Het volgende puntendiagram toont het aantal overtredingen begaan in een bepaalde wedstrijd door basketbalspelers:
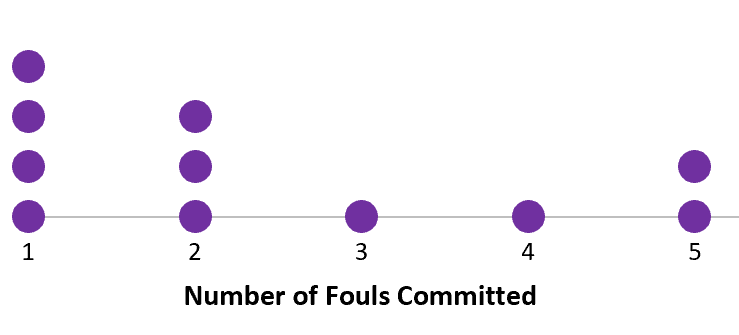
Zo vindt u het centrum en de verdeling van waarden in deze dataset:
Midden : We kunnen de mediaan gebruiken om het “centrum” van de dataset te meten. De mediaan vertegenwoordigt de middelste waarde van de dataset. Om de mediaan voor deze specifieke dataset te vinden, kunnen we elke waarde vermelden en de mediaanwaarde identificeren:
Gegevenswaarden: 1, 1, 1, 1, 2, 2 , 2, 3, 4, 5, 5
De mediaanwaarde in deze gegevensset is 2 .
Spreiding : We kunnen bereik gebruiken om de ‘spreiding’ van waarden over de dataset te meten. Het bereik vertegenwoordigt het verschil tussen de grootste en de kleinste waarde.
In deze dataset kunnen we zien dat de grootste waarde 5 is en de kleinste waarde 1, dus het bereik kan als volgt worden berekend: 5 – 1 = 4 .
Voorbeeld 2: Puntdiagram van testresultaten
Het volgende puntendiagram toont de toetsresultaten van leerlingen in een bepaalde klas:
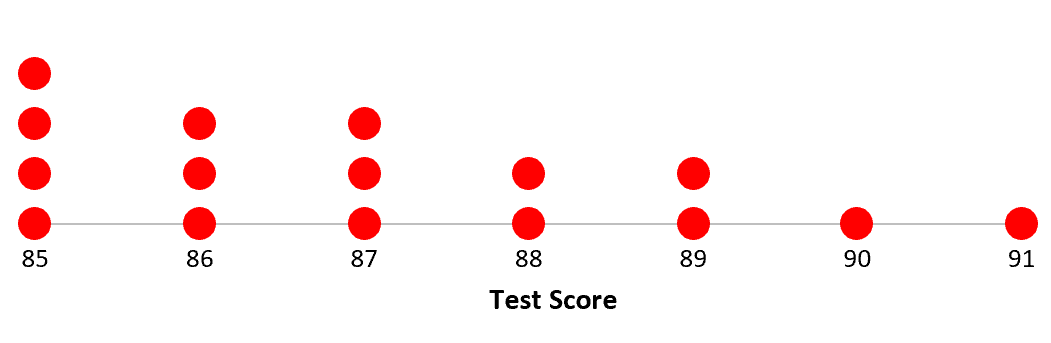
Zo vindt u het centrum en de verdeling van waarden in deze dataset:
Midden : We kunnen de mediaan gebruiken om het “centrum” van de dataset te meten. Om de mediaan voor deze specifieke dataset te vinden, kunnen we elke waarde opsommen en de mediaanwaarde identificeren:
Gegevenswaarden: 85, 85, 85, 85, 86, 86, 86 , 87 , 87, 87, 88, 88, 89, 89, 90, 91
Deze gegevensset heeft een even aantal waarden, dus de mediaan is het gemiddelde van de middelste twee waarden. De mediaan blijkt 87 te zijn.
Spreiding : We kunnen bereik gebruiken om de “spreiding” van waarden in de dataset te meten, die het verschil vertegenwoordigt tussen de grootste en kleinste waarde.
In deze dataset kunnen we zien dat de grootste waarde 91 is en de kleinste 85, dus het bereik kan als volgt worden berekend: 91 – 85 = 6 .
Aanvullende bronnen
In de volgende tutorials wordt uitgelegd hoe u puntplots maakt in verschillende statistische software: