Wat is perfecte multicollineariteit? (definitie & voorbeelden)

In de statistiek treedt multicollineariteit op wanneer twee of meer voorspellende variabelen sterk met elkaar gecorreleerd zijn, zodat ze geen unieke of onafhankelijke informatie verschaffen in het regressiemodel.

Als de mate van correlatie tussen variabelen hoog genoeg is, kan dit problemen veroorzaken bij het aanpassen en interpreteren van het regressiemodel.

Het meest extreme geval van multicollineariteit wordt perfecte multicollineariteit genoemd. Dit gebeurt wanneer twee of meer voorspellende variabelen een exact lineair verband met elkaar hebben.

Stel dat we bijvoorbeeld de volgende gegevensset hebben:

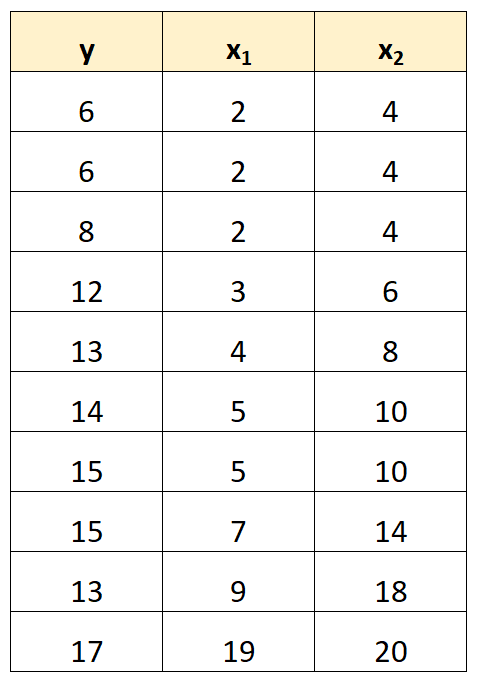
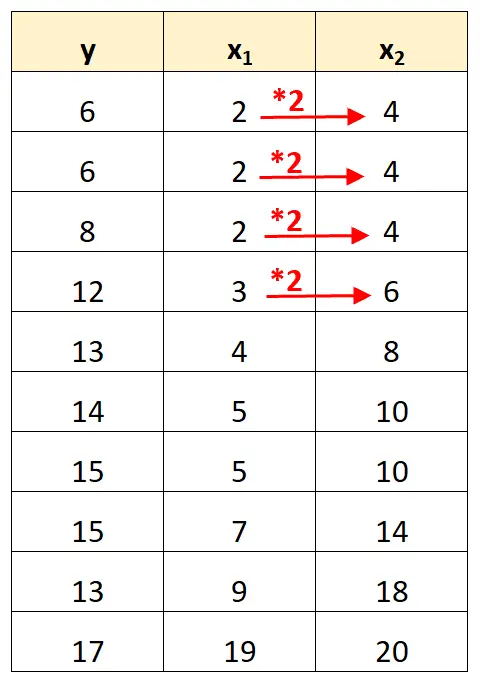
Merk op dat de waarden van de voorspellende variabele x ₂ eenvoudigweg de waarden zijn van x ₁ vermenigvuldigd met 2.

Dit is een voorbeeld van perfecte multicollineariteit .

Het probleem van perfecte multicollineariteit

Wanneer perfecte multicollineariteit aanwezig is in een dataset, kunnen gewone kleinste kwadraten geen schattingen van regressiecoëfficiënten produceren.

Het is inderdaad niet mogelijk om het marginale effect van een voorspellende variabele (x ₁ ) op de responsvariabele (y) te schatten terwijl een andere voorspellende variabele (x ₂ ) constant blijft, omdat x ₂ altijd precies beweegt wanneer x ₁ beweegt.

Kortom, perfecte multicollineariteit maakt het onmogelijk om voor elke coëfficiënt in een regressiemodel een waarde te schatten.

Hoe om te gaan met perfecte multicollineariteit

De eenvoudigste manier om met perfecte multicollineariteit om te gaan, is door een van de variabelen te verwijderen die een exact lineair verband heeft met een andere variabele.

In onze vorige dataset konden we bijvoorbeeld eenvoudigweg x ₂ als voorspellende variabele verwijderen.

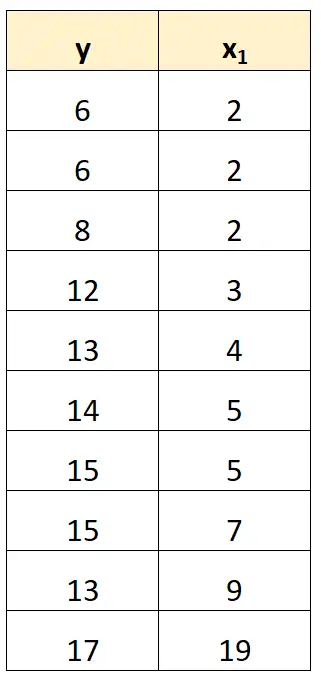
We zouden dan een regressiemodel passen met x ₁ als voorspellende variabele en y als responsvariabele.

Voorbeelden van perfecte multicollineariteit

De volgende voorbeelden tonen de drie meest voorkomende scenario’s van perfecte multicollineariteit in de praktijk.

1. Een voorspellende variabele is een veelvoud van een andere

Laten we zeggen dat we ‚hoogte in centimeters‘ en ‚hoogte in meters‘ willen gebruiken om het gewicht van een bepaalde dolfijnsoort te voorspellen.

Dit is hoe onze dataset er uit zou kunnen zien:

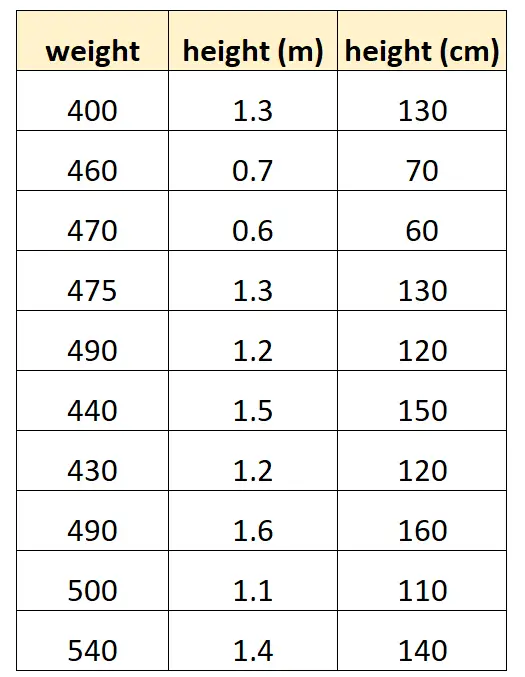
Merk op dat de waarde van „hoogte in centimeters“ eenvoudigweg gelijk is aan „hoogte in meters“ vermenigvuldigd met 100. Dit is een geval van perfecte multicollineariteit.

Als we proberen een meervoudig lineair regressiemodel in R te fitten met behulp van deze dataset, zullen we geen coëfficiëntenschatting kunnen maken voor de voorspellende variabele „meters“:

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. Een voorspellende variabele is een getransformeerde versie van een andere

Laten we zeggen dat we ‚punten‘ en ‚geschaalde punten‘ willen gebruiken om de beoordeling van basketbalspelers te voorspellen.

Stel dat de variabele “geschaalde punten” als volgt wordt berekend:

Geschaalde punten = (punten – μ _punten ) / σ _punten

Dit is hoe onze dataset er uit zou kunnen zien:

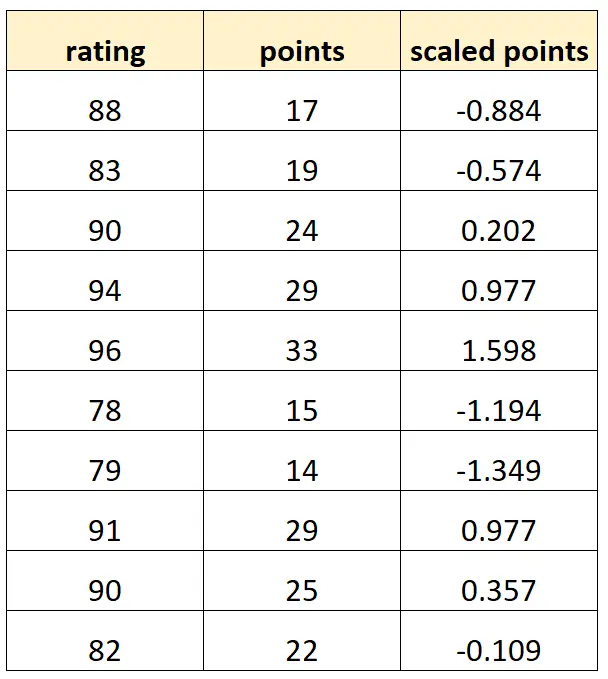
Merk op dat elke „geschaalde punten“-waarde eenvoudigweg een gestandaardiseerde versie van „punten“ is. Dit is een geval van perfecte multicollineariteit.

Als we proberen een meervoudig lineair regressiemodel in R te passen met behulp van deze dataset, zullen we geen coëfficiëntenschatting kunnen maken voor de voorspellende variabele „geschaalde punten“:

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. De dummy-variabele val

Een ander scenario waarin perfecte multicollineariteit kan optreden, staat bekend als de dummy-variabeleval . Dit is wanneer we een categorische variabele in een regressiemodel willen nemen en deze willen converteren naar een „dummyvariabele“ die de waarden 0, 1, 2, enz. aanneemt.

Laten we bijvoorbeeld zeggen dat we de voorspellende variabelen ‚leeftijd‘ en ‚burgerlijke staat‘ willen gebruiken om het inkomen te voorspellen:

Om ‘burgerlijke staat’ als voorspellende variabele te gebruiken, moeten we deze eerst omzetten in een dummyvariabele.

Om dit te doen, kunnen we ‚Single‘ als basiswaarde laten, aangezien dit het vaakst gebeurt, en als volgt waarden van 0 of 1 toewijzen aan ‚Getrouwd‘ en ‚Echtscheiding‘:

Een fout zou zijn om als volgt drie nieuwe dummyvariabelen te maken:

In dit geval is de variabele ‘Single’ een perfecte lineaire combinatie van de variabelen ‘Getrouwd’ en ‘Gescheiden’. Dit is een voorbeeld van perfecte multicollineariteit.

Als we proberen een meervoudig lineair regressiemodel in R te fitten met behulp van deze dataset, zullen we niet in staat zijn om voor elke voorspellende variabele een coëfficiëntenschatting te maken:

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

Aanvullende bronnen

Een gids voor multicollineariteit en VIF in regressie
Hoe VIF in R te berekenen
Hoe VIF in Python te berekenen
Hoe VIF in Excel te berekenen