Hoe log-waarschijnlijkheidswaarden te interpreteren (met voorbeelden)

De log-waarschijnlijkheidswaarde van een regressiemodel is een manier om de goedheid van de pasvorm van een model te meten. Hoe hoger de log-waarschijnlijkheidswaarde, hoe beter het model bij een dataset past.

De waarde van de logwaarschijnlijkheid voor een bepaald model kan variëren van negatief oneindig tot positief oneindig. De werkelijke log-waarschijnlijkheidswaarde voor een bepaald model is over het algemeen betekenisloos, maar is nuttig voor het vergelijken van twee of meer modellen .

In de praktijk passen we vaak meerdere regressiemodellen aan een dataset toe en kiezen we het model met de hoogste logwaarschijnlijkheidswaarde als het model dat het beste bij de gegevens past.

Het volgende voorbeeld laat zien hoe log-waarschijnlijkheidswaarden voor verschillende regressiemodellen in de praktijk kunnen worden geïnterpreteerd.

Voorbeeld: Log-waarschijnlijkheidswaarden interpreteren

Laten we zeggen dat we de volgende dataset hebben die het aantal slaapkamers, het aantal badkamers en de verkoopprijzen van 20 verschillende woningen in een bepaalde buurt laat zien:

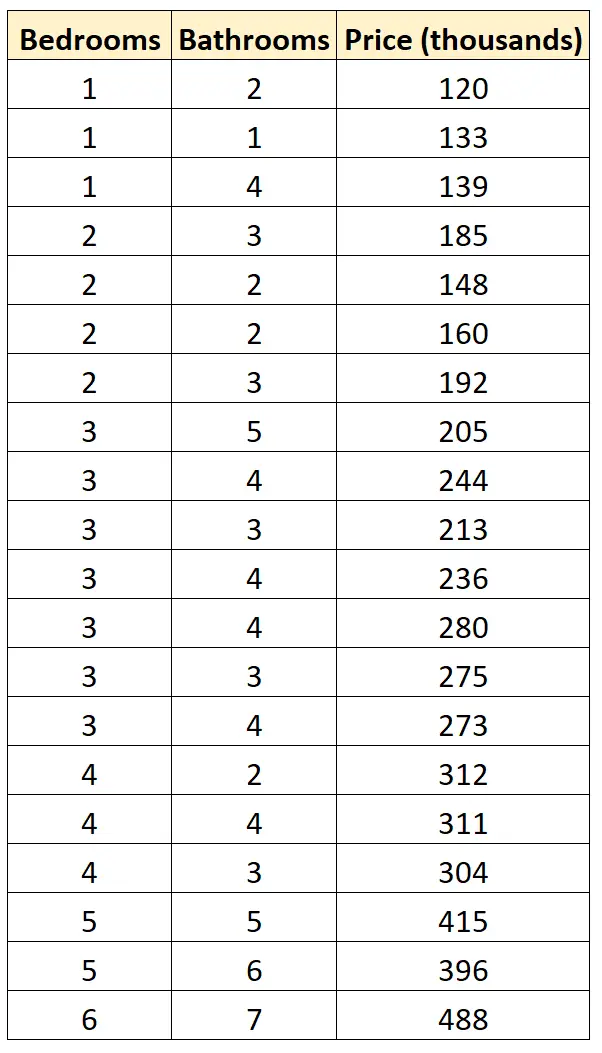
Stel dat we de volgende twee regressiemodellen willen passen en bepalen welke het beste bij de gegevens past:

Model 1 : Prijs = β ₀ + β ₁ (aantal kamers)

Model 2 : Prijs = β ₀ + β ₁ (aantal badkamers)

De volgende code laat zien hoe u elk regressiemodel kunt aanpassen en de logwaarschijnlijkheidswaarde van elk model in R kunt berekenen:

 #define data
df <- data. frame (beds=c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
                        3, 3, 3, 3, 4, 4, 4, 5, 5, 6),
                 baths=c(2, 1, 4, 3, 2, 2, 3, 5, 4, 3,
                         4, 4, 3, 4, 2, 4, 3, 5, 6, 7),
                 price=c(120, 133, 139, 185, 148, 160, 192, 205, 244, 213,
                         236, 280, 275, 273, 312, 311, 304, 415, 396, 488))

#fitmodels
model1 <- lm(price~beds, data=df)
model2 <- lm(price~baths, data=df)

#calculate log-likelihood value of each model
logLik(model1)

'log Lik.' -91.04219 (df=3)

logLik(model2)

'log Lik.' -111.7511 (df=3)

Het eerste model heeft een hogere logwaarschijnlijkheidswaarde ( -91,04 ) dan het tweede model ( -111,75 ), wat betekent dat het eerste model beter aansluit bij de gegevens.

Voorzorgsmaatregelen voor het gebruik van log-waarschijnlijkheidswaarden

Bij het berekenen van log-waarschijnlijkheidswaarden is het belangrijk op te merken dat het toevoegen van extra voorspellende variabelen aan een model bijna altijd de log-waarschijnlijkheidswaarde zal verhogen, zelfs als de extra voorspellende variabelen niet statistisch significant zijn.

Dit betekent dat u de logwaarschijnlijkheidswaarden tussen twee regressiemodellen alleen moet vergelijken als elk model hetzelfde aantal voorspellende variabelen heeft.

Als u modellen met verschillende aantallen voorspellende variabelen wilt vergelijken, kunt u een waarschijnlijkheidsratiotest uitvoeren om de goedheid van de pasvorm van twee geneste regressiemodellen te vergelijken.

Aanvullende bronnen

Hoe de functie lm() te gebruiken om lineaire modellen in R te passen
Hoe een waarschijnlijkheidsratiotest uit te voeren in R