Bètadistributie

Von Dr.benjamin anderson August 4, 2023 Waarschijnlijkheid Keine Kommentare

In dit artikel wordt uitgelegd wat bètadistributie is en waarvoor het wordt gebruikt. Op dezelfde manier kunt u de bètaverdelingsgrafiek en de eigenschappen van dit type kansverdeling zien.

Wat is de bètaverdeling?

De bètaverdeling is een waarschijnlijkheidsverdeling gedefinieerd op het interval (0,1) en geparametriseerd door twee positieve parameters: α en β. Met andere woorden: de waarden van de bètaverdeling zijn afhankelijk van de parameters α en β.

Het belangrijkste kenmerk van de bètaverdeling is daarom dat de vorm ervan kan worden bepaald door de parameters α en β. Bovendien wordt de bètaverdeling gebruikt om willekeurige variabelen te definiëren waarvan de waarde tussen 0 en 1 ligt.

Er zijn verschillende notaties die aangeven dat een continue willekeurige variabele wordt bepaald door een bètaverdeling. De meest voorkomende zijn:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}$

In de statistieken heeft de bètadistributie zeer uiteenlopende toepassingen. De bètaverdeling wordt bijvoorbeeld gebruikt om variaties in percentages in verschillende steekproeven te bestuderen. Op dezelfde manier wordt bij projectbeheer bètadistributie gebruikt om Pert-analyse uit te voeren.

Bèta-distributieplot

Rekening houdend met de definitie van bètaverdeling, worden hieronder de dichtheidsfunctie en de waarschijnlijkheidsverdelingsfunctie van de bètaverdeling weergegeven.

Hieronder kunt u zien hoe de dichtheidsfunctiegrafiek van de bètaverdeling varieert afhankelijk van de parameters α en β.

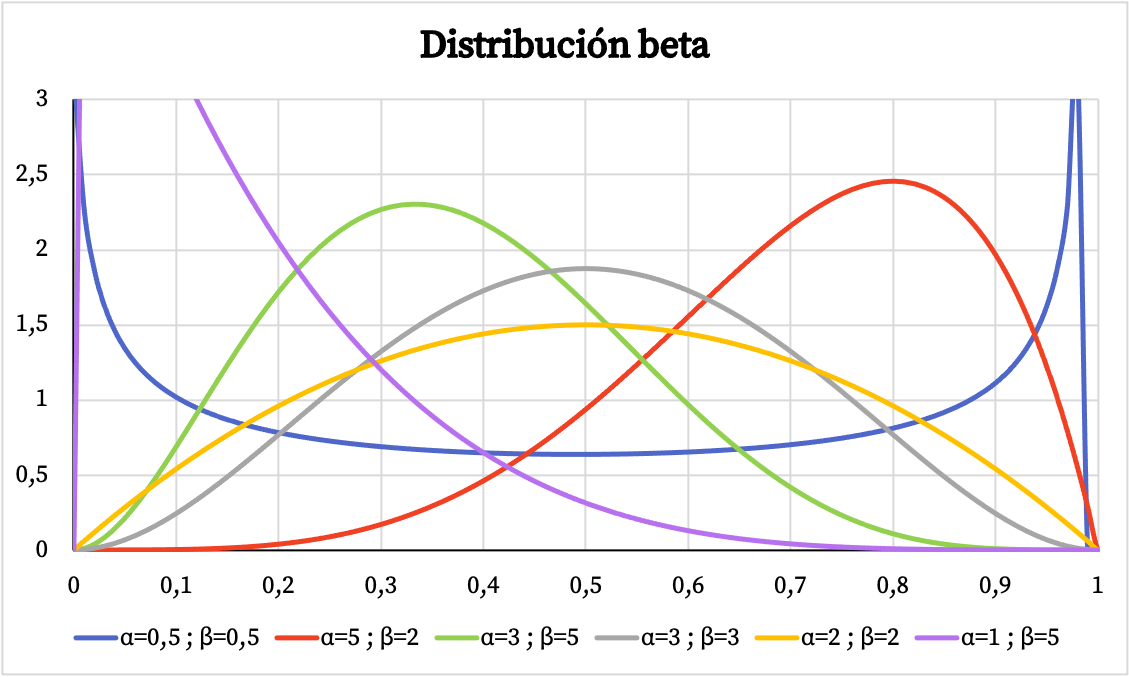
Op dezelfde manier ziet u hieronder de grafische weergave van de cumulatieve waarschijnlijkheid van de bètaverdeling op basis van de parameters α en β.

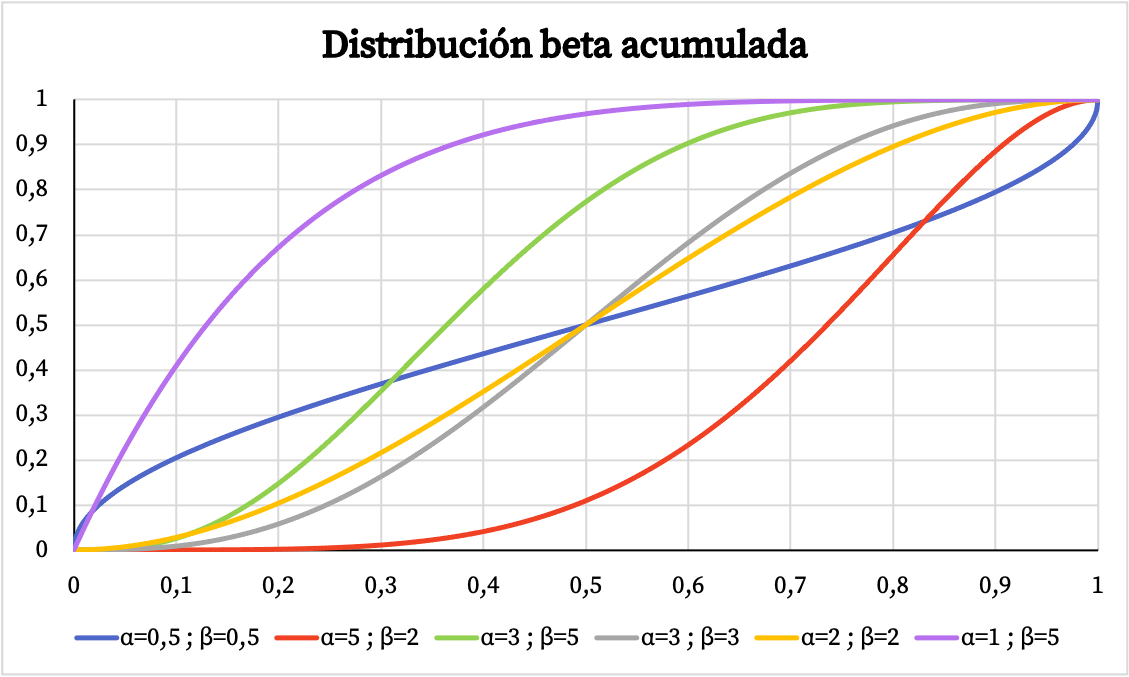
Kenmerken van de bètaverdeling

In deze sectie zullen we zien wat de belangrijkste kenmerken van de bètadistributie zijn.

De parameters α en β van de bètaverdeling zijn reële en positieve getallen.

$\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}“ title=“Rendered by QuickLaTeX.com“ height=“54″ width=“44″ style=“vertical-align: 0px;“></p> </p> <ul> <li> Het domein van de bètaverdeling varieert van 0 tot 1, de twee uitersten zijn niet inbegrepen.</li> </ul> <p class=$ $x\in (0,1)$

Het gemiddelde van de bètaverdeling is gelijk aan alfa gedeeld door de som alfa plus bèta.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}$

De variantie van de bètaverdeling kan worden berekend met behulp van de volgende formule:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}$

Voor waarden van alfa en bèta groter dan 1 kan de bètaverdelingsmodus eenvoudig worden gevonden met de volgende uitdrukking:

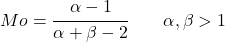
$Mo=\cfrac{\alpha-1}{\alpha+\beta-2}\qquad \alpha,\beta>1″ title=“Rendered by QuickLaTeX.com“ height=“42″ width=“225″ style=“vertical-align: -16px;“></p> </p> <ul> <li> De dichtheidsfunctie van de bètaverdeling is als volgt:</li> </ul> <p class=$ $\displaystyle P[X=x]=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$

Waarbij B(α,β) de bètafunctie is, die wordt gedefinieerd als:

$\displaystyle B(\alpha,\beta)=\int_0^1x^{\alpha-1}(1-x)^{\beta-1}dx$

De cumulatieve waarschijnlijkheidsfunctie van de bètaverdeling is:

$\displaystyle P[X\leq x]=\frac{B(x;\alpha,\beta)}{B(\alpha,\beta)}$

Waarbij B(x;α,β) de onvolledige bètafunctie is, gedefinieerd als:

$\displaystyle B(x;\,a,b) = \int_0^x t^{a-1}\,(1-t)^{b-1}\,dt$

Als X een variabele is die wordt gedefinieerd door een bètaverdeling, dan is 1-X een variabele die wordt gedefinieerd door een bètaverdeling waarvan de alfa- en bètaparameters respectievelijk de bèta- en alfaparameters zijn van de oorspronkelijke bètaverdeling.

$X\sim B(\alpha,\beta) \ \color{orange}\bm{\longrightarrow}\color{black} \ 1-X\sim B(\beta,\alpha)$

Als de alfa- en bètaparameters van de bètaverdeling beide gelijk zijn aan 1, dan is de verdeling equivalent aan een uniforme verdeling van parameters 0 en 1.

$X\sim B(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim U(0,1)$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Wat is de bètaverdeling?

Bèta-distributieplot

Kenmerken van de bètaverdeling

Über den Autor

Dr.benjamin anderson

Einen Kommentar hinzufügen