Gamma-distributie

In dit artikel wordt uitgelegd wat de gammaverdeling is en waarvoor deze wordt gebruikt. Zo vindt u de definitie van de gammaverdeling, de eigenschappen ervan en hoe de grafische weergave ervan eruit ziet.

Wat is de gammaverdeling?

De gammaverdeling is een continue waarschijnlijkheidsverdeling die wordt gedefinieerd door twee karakteristieke parameters, α en λ. Met andere woorden, de gammaverdeling hangt af van de waarde van de twee parameters: α is de vormparameter en λ is de schaalparameter.

Het symbool voor de gammaverdeling is de Griekse hoofdletter Γ. Dus als een willekeurige variabele een gammaverdeling volgt, wordt deze als volgt geschreven:

De gammaverdeling kan ook worden geparametriseerd met behulp van de vormparameter k = α en de inverse schaalparameter θ = 1/λ. In alle gevallen zijn de twee parameters die de gammaverdeling bepalen positieve reële getallen.

Meestal wordt de gammaverdeling gebruikt om naar rechts scheve gegevenssets te modelleren, zodat er een grotere concentratie van gegevens aan de linkerkant van de grafiek is. De gammaverdeling wordt bijvoorbeeld gebruikt om de betrouwbaarheid van elektrische componenten te modelleren.

Gamma-verdelingsdiagram

De grafiek van de gammaverdeling hangt af van de waarden van de karakteristieke parameters. Hieronder kunt u zien hoe de dichtheidsfunctie van de gammaverdeling varieert afhankelijk van de vormparameter en de schaalparameter.

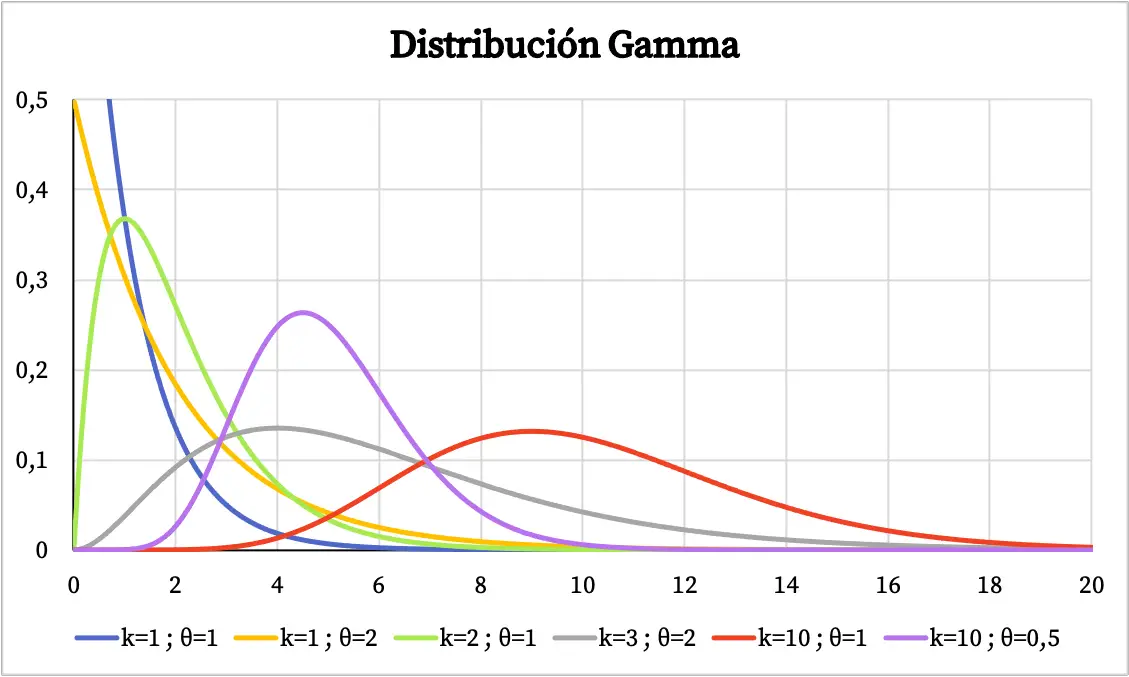
Aan de andere kant kunt u hieronder de grafiek zien van de cumulatieve waarschijnlijkheidsfunctie van de gammaverdeling:

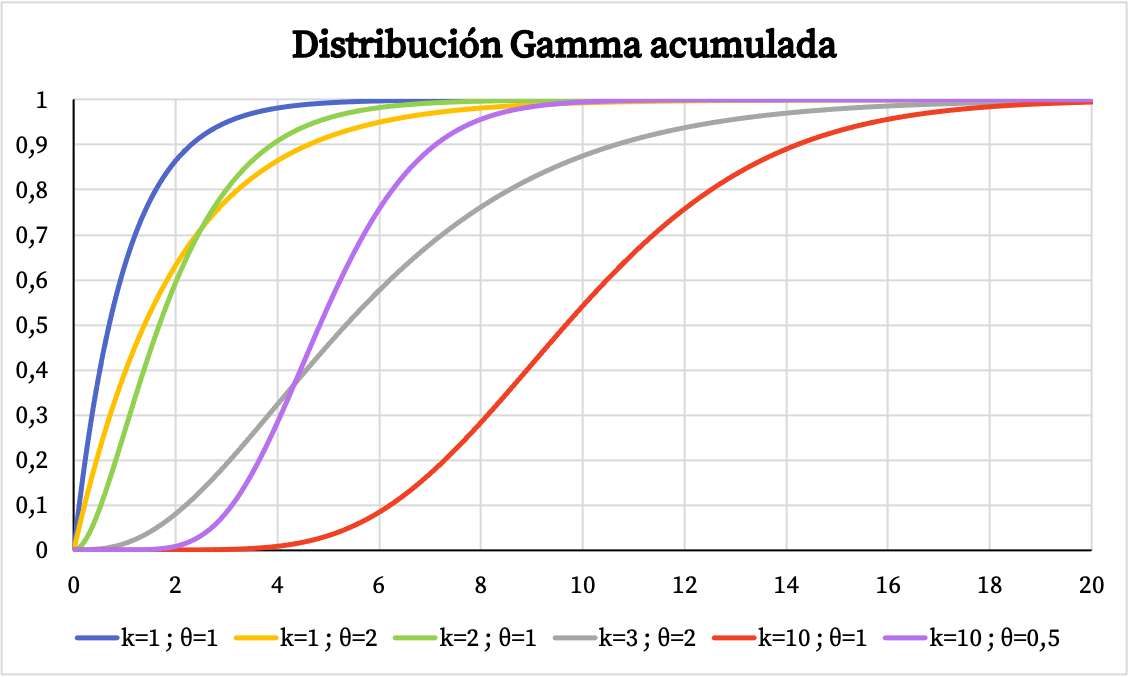
Kenmerken van de gammaverdeling

We zullen dan zien wat de kenmerken van de gammaverdeling zijn.

• De grafiek van de gammaverdeling wordt volledig bepaald door de twee karakteristieke parameters: α is de vormparameter en λ is de schaalparameter.

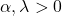
• Het gemiddelde van de gammaverdeling is gelijk aan de verhouding tussen de vormparameter en de schaalparameter, dwz α/λ.

• De variantie van de gammaverdeling is equivalent aan de vormparameter gedeeld door het kwadraat van de schaalparameter.

• Voor waarden van α kleiner dan 1 is de modus 0. Maar als α gelijk is aan of groter is dan 1, kan de modus van de gammaverdeling worden berekend met de volgende formule:

• De formule voor de dichtheidsfunctie van de gammaverdeling is:

Waarbij Γ de gammafunctie is, die wordt gedefinieerd als:

• De formule voor de cumulatieve verdeling van een willekeurige variabele gedefinieerd door een gammaverdeling is als volgt:

• Als de vormparameter α gelijk is aan 1, dan is de gammaverdeling equivalent aan een exponentiële verdeling met dezelfde schaalparameter λ.

• Wanneer de schaalparameter λ een gemiddelde is, dan is de gammaverdeling een speciaal geval van de chikwadraatverdeling .