Discrete uniforme distributie

In dit artikel wordt uitgelegd wat de discrete uniforme verdeling is en wat de karakteristieke formule ervan is. Op dezelfde manier kunt u de grafische weergave zien van de discrete uniforme verdeling en wat de eigenschappen ervan zijn.

Wat is discrete uniforme verdeling?

Discrete uniforme verdeling is een discrete kansverdeling waarin alle waarden gelijkwaardig zijn, dat wil zeggen dat in een discrete uniforme verdeling alle waarden dezelfde waarschijnlijkheid hebben om te voorkomen.

De worp van een dobbelsteen kan bijvoorbeeld worden gedefinieerd met een discrete uniforme verdeling, aangezien alle mogelijke uitkomsten (1, 2, 3, 4, 5 of 6) dezelfde waarschijnlijkheid van voorkomen hebben.

Over het algemeen heeft een discrete uniforme verdeling twee karakteristieke parameters, a en b , die het bereik van mogelijke waarden definiëren die de verdeling kan aannemen. Wanneer een variabele dus wordt gedefinieerd door een discrete uniforme verdeling, wordt deze geschreven Uniform(a,b) .

De discrete uniforme verdeling kan worden gebruikt om willekeurige experimenten te beschrijven, want als alle uitkomsten dezelfde waarschijnlijkheid hebben, betekent dit dat het experiment willekeurig is.

Discrete uniforme distributieformule

Nu we de definitie van de discrete uniforme verdeling kennen, zullen we zien wat de formule is waarmee we de waarschijnlijkheid van het verschijnen van de waarden van een dergelijke verdeling kunnen berekenen.

De waarschijnlijkheidsfunctie van een discrete uniforme verdeling is constant en de waarde ervan is gelijk aan één over het totale aantal mogelijke uitkomsten. De formule voor de discrete uniforme verdeling is dus als volgt:

Aan de andere kant is de formule voor de cumulatieve waarschijnlijkheidsfunctie van de discrete uniforme verdeling als volgt:

Goud

En

zijn de karakteristieke parameters van de discrete uniforme verdeling.

Discreet uniform distributiediagram

Omdat de discrete uniforme verdeling slechts bepaalde waarden in een interval kan aannemen, bestaat de grafische weergave ervan uit punten. Bovendien zijn alle kansen gelijk, dus alle punten in de discrete uniforme verdeling hebben dezelfde verticale coördinaat.

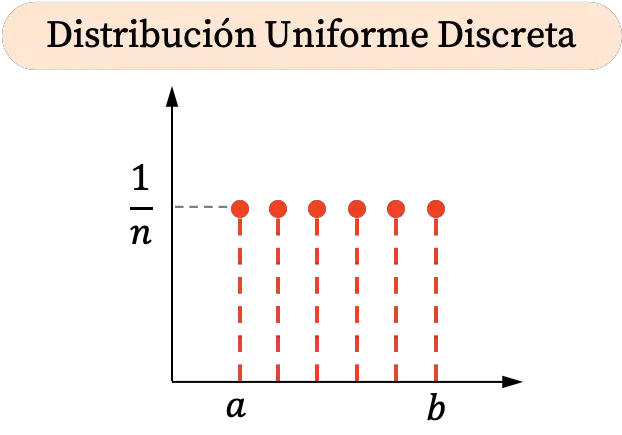
Aan de andere kant is de cumulatieve waarschijnlijkheidsgrafiek van de discrete uniforme verdeling als volgt:

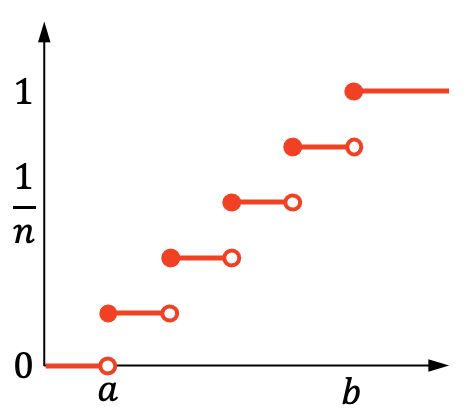
Kenmerken van de discrete uniforme verdeling

De discrete uniforme verdeling heeft de volgende kenmerken:

• De discrete uniforme verdeling wordt gedefinieerd door twee geheeltallige parameters, a en b , die het bereik van mogelijke waarden van de verdeling bepalen.

• Het gemiddelde van een discrete uniforme verdeling is gelijk aan de som van de twee karakteristieke parameters gedeeld door twee.

• De mediaan van een discrete uniforme verdeling is gelijk aan het gemiddelde, dus wordt berekend met dezelfde uitdrukking:

• De variantie van een discrete uniforme verdeling is gelijk aan het kwadraat van het totale aantal uitkomsten min één gedeeld door twaalf.

• De discrete uniforme verdeling is symmetrisch ten opzichte van het gemiddelde, daarom is de scheefheidscoëfficiënt van deze waarschijnlijkheidsverdeling nul.

• De kurtosis van de discrete uniforme verdeling kan worden berekend met behulp van de volgende uitdrukking:

Discrete uniforme distributie en continue uniforme distributie

Ten slotte zullen we zien wat het verschil is tussen een discrete uniforme verdeling en een continue uniforme verdeling, aangezien het twee vergelijkbare soorten waarschijnlijkheidsverdelingen zijn, maar met een substantieel verschil.

Het verschil tussen een discrete uniforme verdeling en een continue uniforme verdeling ligt in hun mogelijke waarden. De discrete uniforme verdeling kan alleen bepaalde waarden in een interval aannemen, terwijl de continue uniforme verdeling elke waarde kan aannemen in het interval waarin deze is gedefinieerd.

Over het algemeen kunnen discrete uniforme verdelingen alleen gehele waarden aannemen, terwijl continue uniforme verdelingen ook decimale waarden kunnen aannemen.