De wet van benford
In dit artikel wordt uitgelegd wat de wet van Benford is. Bovendien kunt u zien hoe de wet van Benford werd ontdekt en wat de toepassingen van deze statistische wet zijn.
Wat is de wet van Benford?
De wet van Benford , ook wel de wet van het eerste cijfer genoemd, is een statistische wet die zegt dat de kans dat het eerste cijfer van een gegeven een 1 is, groter is dan de kans dat het een ander getal is.
Met andere woorden, de wet van Benford zegt dat in een reeks numerieke gegevens die in het echte leven bestaan, het getal 1 het meest herhaalde getal is als eerste cijfer van de gegevens.
Bovendien geldt: hoe hoger het getal, hoe kleiner de kans dat het op de eerste plaats eindigt. Daarom is het eerste getal waarschijnlijker een 1 dan een 2, maar 2 is waarschijnlijker dan 3, 3 is waarschijnlijker dan 4, enzovoort.
De wet van Benford dankt zijn naam aan de Amerikaan Frank Benford. Hoewel hij het niet heeft uitgevonden, heeft Benford deze statistische regel gepopulariseerd. Hieronder zullen we de oorsprong van de wet van Benford zien.
De wetsformule van Benford
De wet van Benford stelt dat de kans dat het eerste cijfer een bepaald getal is, gelijk is aan de logaritme van één plus één boven dat getal.
De formule voor de wet van Benford is daarom als volgt:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a77defb5b209293a074ac2bee02c2e07_l3.png)
Daarom kunnen we uit de formule van de wet van Benford voor elk getal de waarschijnlijkheid afleiden dat dit het eerste cijfer van een gegevensitem is. In de volgende tabel ziet u de percentages van alle kansen:
| Figuur | Waarschijnlijkheid dat wees het eerste getal |
|---|---|
| 1 | 30,1% |
| 2 | 17,6% |
| 3 | 12,5% |
| 4 | 9,7% |
| 5 | 7,9% |
| 6 | 6,7% |
| 7 | 5,8% |
| 8 | 5,1% |
| 9 | 4,6% |
Bovendien ziet u hieronder een histogram waarin alle kansen van de wet van Benford grafisch worden weergegeven:
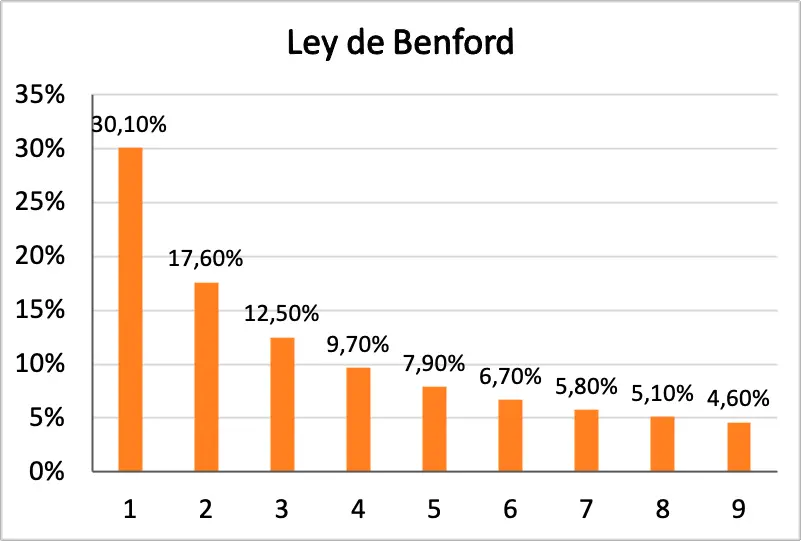
Geschiedenis van de wet van Benford
In 1881 leidde wiskundige Simon Newcomb de wet van Benford af toen hij ontdekte dat de eerste pagina’s van logaritmetabellen aanzienlijk meer werden gebruikt dan de laatste pagina’s. Dat betekende dat de eerste cijfers van getallen niet even waarschijnlijk zijn, maar dat 1 vaker voorkwam dan 2, 2 vaker voorkwam dan 3, enzovoort tot en met 9.
Newcomb liet echter geen statistisch bewijs achter dat deze regel werd gevolgd; hij trok eenvoudigweg een conclusie uit de slijtage van de logaritmische tabellen.
Later, specifiek in 1938, deed natuurkundige Frank Benford dezelfde waarneming en voerde hij ook een experiment uit om dit empirisch te verifiëren. Op een statistische gegevensset van 20.229 waarden uit 20 verschillende monsters voerde hij een onderzoek uit naar het eerste cijfer van elke gegevens. Op basis van de resultaten demonstreerde hij dus dat aan de wet van Benford was voldaan en leidde hij de formule af waarmee hij de waarschijnlijkheid kon berekenen dat het eerste cijfer een bepaald getal was (we hebben deze formule hierboven gezien).
Kortom, hoewel de wet van Benford voor het eerst werd ontdekt door Simon Newcomb, is hij vernoemd naar Frank Benford omdat hij degene was die deze statistische wet heeft geverifieerd.
Toepassingen van de wet van Benford
De wet van Benford is een statistische wet die toepassingen vindt op zeer verschillende gebieden. De wet van Benford wordt bijvoorbeeld veel gebruikt in de economie, de biologie en zelfs de politiek.
In de economie wordt de wet van Benford vaak gebruikt om datamanipulatie op te sporen, omdat als een dataset niet voldoet aan de wet van Benford, dit aangeeft dat de gegevens zijn gemanipuleerd. Deze wet wordt bijvoorbeeld gebruikt om mogelijke gevallen van belastingfraude op te sporen.
Opgemerkt moet worden dat de wet van Benford niet wordt gebruikt om de waarheid van willekeurige verschijnselen aan te tonen, aangezien de resultaten gelijkwaardig zijn. De regel van Benford kan dus niet worden gebruikt om loterijresultaten te verifiëren.
Aan de andere kant kan in de genetica de wet van Benford worden gebruikt om verschillen in genoomlengte tussen verschillende soorten organismen te analyseren.
Ten slotte zijn er ook pogingen ondernomen om kiezersfraude op te sporen door de wet van Benford toe te passen, hoewel het nut ervan in dit geval in twijfel wordt getrokken.