Pareto-distributie
In dit artikel wordt uitgelegd wat Pareto-distributie in statistieken is en waarvoor het wordt gebruikt. U kunt ook de Pareto-verdelingsgrafiek en de eigenschappen van dit type kansverdeling zien.
Wat is Pareto-verdeling?
De Pareto-verdeling is een continue kansverdeling die in statistieken wordt gebruikt om het Pareto-principe te modelleren. Daarom is de Pareto-verdeling een kansverdeling die een paar waarden heeft waarvan de waarschijnlijkheid van voorkomen veel groter is dan de rest van de waarden.
Bedenk dat de wet van Pareto, ook wel de 80-20-regel genoemd, een statistisch principe is dat zegt dat het grootste deel van de oorzaak van een fenomeen te wijten is aan een klein deel van de bevolking.
De Pareto-verdeling heeft twee karakteristieke parameters: de schaalparameter x m en de vormparameter α.
Oorspronkelijk werd de Pareto-verdeling gebruikt om de verdeling van de rijkdom binnen de bevolking te beschrijven, omdat het grootste deel ervan te danken was aan een klein deel van de bevolking. Maar momenteel heeft de Pareto-verdeling vele toepassingen, bijvoorbeeld in de kwaliteitscontrole, in de economie, in de wetenschap, op sociaal gebied, enz.
De Pareto-verdeling is vernoemd naar de econoom Vilfredo Pareto, die de verdeling formuleerde. Hij is echter vooral bekend van de Pareto-grafiek.
Pareto-verdelingstabel
Nu we de definitie van Pareto-verdeling kennen, gaan we eens kijken naar verschillende voorbeelden van Pareto-verdelingen die grafisch worden weergegeven.
Hieronder kunt u dus zien hoe de grafiek van de dichtheidsfunctie van de Pareto-verdeling eruit ziet, afhankelijk van de karakteristieke waarden:
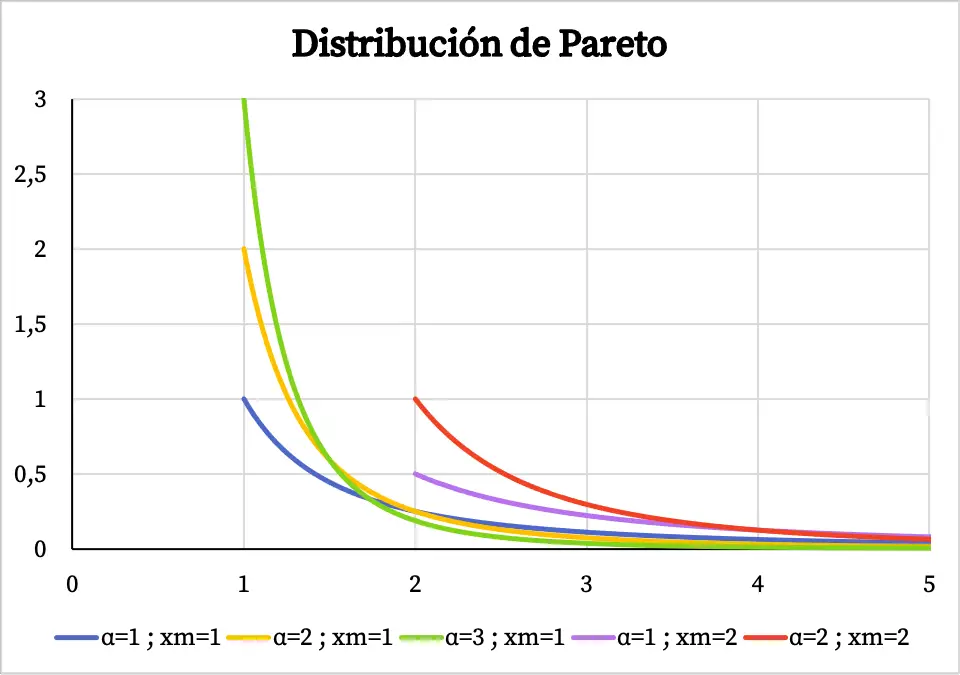
Merk op dat het domein van de Pareto-verdeling van de waarde x m naar +∞ gaat, en daarom bestaat de dichtheidsfunctie niet vóór de waarde van x m .
Aan de andere kant is de grafiek van de cumulatieve waarschijnlijkheidsfunctie van de Pareto-verdeling als volgt:
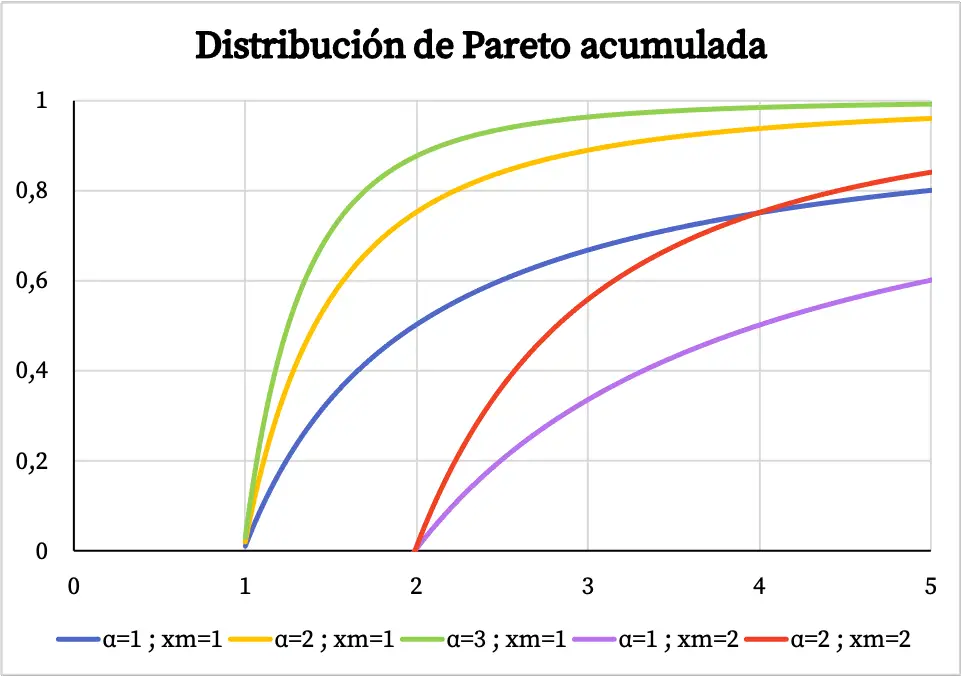
Kenmerken van de Pareto-verdeling
Hieronder staan de belangrijkste kenmerken van de Pareto-verdeling met betrekking tot de waarschijnlijkheidstheorie en statistiek.
- De Pareto-verdeling heeft twee karakteristieke parameters die de curve definiëren: de schaalparameter x m en de vormparameter α.
- Het domein van de Pareto-verdeling bestaat uit alle reële getallen vanaf de schaalparameter tot plus oneindig.
- Als α groter is dan 1, is het gemiddelde van de Pareto-verdeling gelijk aan het product van α maal x m en α min 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=“Rendered by QuickLaTeX.com“ height=“34″ width=“214″ style=“vertical-align: -12px;“></p>
</p>
<ul>
<li> De variantie van de Pareto-verdeling hangt af van de twee karakteristieke parameters van de verdeling en wordt berekend met de volgende formule:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
![\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0dc2c772a0a0662ad05f8b22c3cf1ba1_l3.png "Rendered by QuickLaTeX.com")
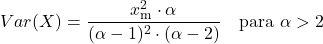
- De modus van de Pareto-verdeling is equivalent aan de schaalparameter x m van de verdeling.
- De formule voor de dichtheidsfunctie van de Pareto-verdeling is:
![\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m](https://statorials.org/wp-content/ql-cache/quicklatex.com-1e182771cfe3bf9a145a2ee59b9c7eeb_l3.png "Rendered by QuickLaTeX.com")
- Op dezelfde manier is de formule voor de cumulatieve waarschijnlijkheidsfunctie van de Pareto-verdeling:
![\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha](https://statorials.org/wp-content/ql-cache/quicklatex.com-480adc7841b7c72cb4bfecb446ed3fab_l3.png "Rendered by QuickLaTeX.com")
- De asymmetriecoëfficiënt van de Pareto-verdeling hangt alleen af van de vormparameter α en de uitdrukking ervan is:
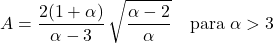
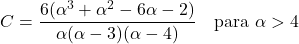
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder