5 voorbeelden van het berekenen van de verwachte waarde in het echte leven

De verwachte waarde is een waarde die ons het verwachte gemiddelde vertelt dat een willekeurige variabele in een oneindig aantal pogingen zal aannemen.

Om de verwachte waarde van een gebeurtenis te berekenen, gebruiken we de volgende formule:

Verwachte waarde = Σx * P(x)

Goud:

• x : gegevenswaarde
• P(x) : Waarschijnlijkheid van waarde

Deze formule lijkt misschien een beetje verwarrend, maar wordt logischer als je hem ziet gebruikt in de context van voorbeelden uit de echte wereld.

De volgende voorbeelden laten zien hoe de verwachte waarde wordt berekend in vijf verschillende praktijksituaties.

Voorbeeld 1: Investeringen

Verwachte waarde wordt door handelsbedrijven vaak gebruikt om de verwachte winst of verlies van een belegging te bepalen.

Stel bijvoorbeeld dat een bepaalde belegging een jaarlijks rendement van 5% kan genereren met een waarschijnlijkheid van 0,95, maar ook een jaarlijks rendement van -20% kan genereren met een waarschijnlijkheid van 0,05.

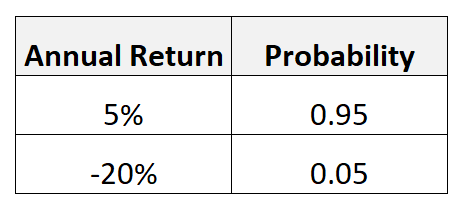
De verwachte waarde van deze investering berekenen wij als volgt:

• Verwachte waarde = 5%*.95 + (-20%)*.05 = 3,75%

Deze bijzondere investering heeft een positieve verwachtingswaarde.

Dit betekent dat als we een oneindig aantal keren in deze specifieke belegging zouden investeren, we op lange termijn een gemiddeld jaarlijks rendement van 3,75% zouden verwachten.

Voorbeeld 2: Weer

De verwachtingswaarde wordt door landbouwbedrijven vaak gebruikt om de verwachte hoeveelheid regen te bepalen die in een bepaald seizoen zal vallen.

Stel bijvoorbeeld dat er een kans van 20% is op 1 inch regen, een kans van 70% op 2 inch regen en een kans van 10% op 7,5 cm regen.

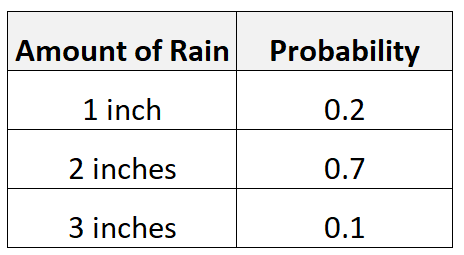
De verwachte waarde van de hoeveelheid regen berekenen we als volgt:

• Verwachte waarde = 0,2*1 + 0,7*2 + 0,1*3 = 1,9 inch

Voorbeeld 3: Kansspelen

Verwachte waarde wordt vaak door spelers gebruikt om te bepalen hoeveel ze potentieel kunnen winnen in een bepaald spel.

Stel bijvoorbeeld dat er in een bepaald spel een kans van 5% is om €100 te winnen, een kans van 50% om €0 te winnen en een kans van 45% om €20 te verliezen.

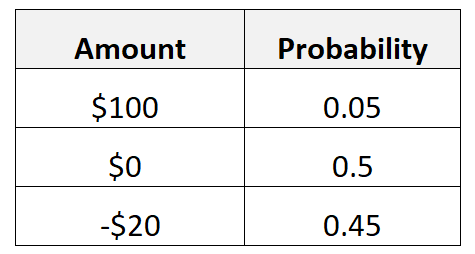
De verwachte waarde van de winst berekenen we als volgt:

• Verwachte waarde = 0,05*100$ + 0,5*0$ + 0,45*(-20$) = -4$

Dit betekent dat als we dit spel een oneindig aantal keren zouden spelen, we gemiddeld € 4 zouden verliezen elke keer dat we spelen.

Voorbeeld 4: Zakelijk

Verwachte waarde wordt vaak door bedrijven gebruikt om het verwachte rendement op advertentie-uitgaven te berekenen.

Stel bijvoorbeeld dat er voor een bepaalde advertentie een kans van 10% is op een rendement van € 5, een kans van 30% op een rendement van € 2, en een kans van 60% op een rendement van -€ 8.

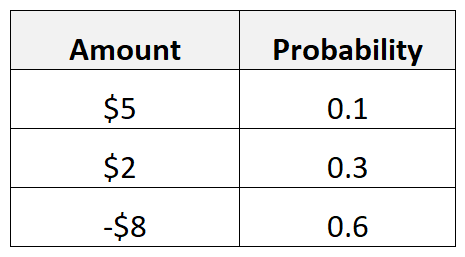
We berekenen de verwachte waarde van de advertentie als volgt:

• Verwachte waarde = 0,1*5$ + 0,3*2$ + 0,6*(-8$) = -3,70$

Deze specifieke advertentie heeft een negatieve verwachtingswaarde.

Dit betekent dat als het bedrijf deze specifieke advertentie een oneindig aantal keren zou gebruiken, het gemiddeld €3,70 per keer zou verliezen.

Voorbeeld 5: Ondernemerschap

Verwachte waarde wordt vaak door individuen gebruikt om te beslissen of ze al dan niet willen ondernemen.

Stel bijvoorbeeld dat iemand gelooft dat als hij zijn baan opzegt en als zelfstandige gaat werken, hij een kans van 60% heeft om in zijn eerste jaar €20.000 te verdienen, een kans van 30% om €60.000 te verdienen en een kans van 10% om €20.000 te winnen. $ 0.

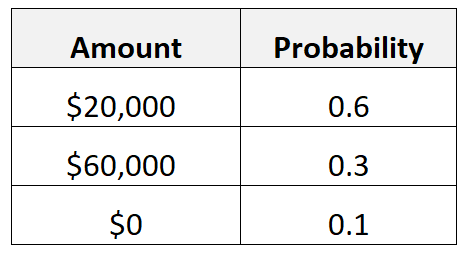
De verwachte waarde van hun inkomen tijdens het eerste jaar van ondernemerschap berekenen we als volgt:

• Verwachte waarde = 0,6*$20.000 + 0,3*$60.000 + 0,1*$0 = $30.000

Afhankelijk van of dit bedrag voldoende is of niet, kan het individu er vervolgens voor kiezen om zijn huidige baan te behouden of deze te verlaten.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over de verwachte waarde:

Hoe de verwachte waarde in Excel te berekenen
Hoe u de verwachte waarde in R kunt berekenen (met voorbeelden)
Verwachte waarde versus gemiddeld: wat is het verschil?