Variatie binnen of tussen groepen in anova
Een eenrichtings-ANOVA wordt gebruikt om te bepalen of de gemiddelden van drie of meer onafhankelijke groepen al dan niet gelijk zijn.
Een eenrichtings-ANOVA gebruikt de volgende nul- en alternatieve hypothesen :
- H 0 : Alle groepsgemiddelden zijn gelijk.
- H A : Minstens één groepsgemiddelde verschilt van de andere.
Elke keer dat u een eenrichtings-ANOVA uitvoert, krijgt u een samenvattende tabel die er als volgt uitziet:
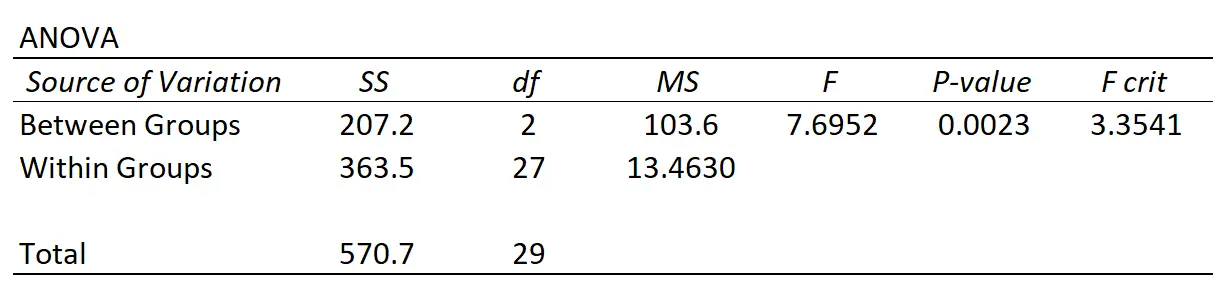
We kunnen zien dat er twee verschillende bronnen van variatie zijn die een ANOVA meet:
Variatie tussen groepen : de totale variatie tussen het gemiddelde van elke groep en het algehele gemiddelde.
Variatie binnen de groep : de totale variatie van individuele waarden in elke groep en hun groepsgemiddelde.
Als de variatie tussen groepen hoog is ten opzichte van de variatie binnen de groep, dan zal de F-statistiek van de ANOVA hoger zijn en de overeenkomstige p-waarde lager, waardoor het waarschijnlijker wordt dat de nulhypothese zal worden verworpen op basis waarvan de groepsgemiddelden zijn gelijk.
Het volgende voorbeeld laat zien hoe u in de praktijk de variatie tussen en binnen de groep kunt berekenen voor eenrichtings-ANOVA.
Voorbeeld: Variatie berekenen binnen een groep en tussen groepen in ANOVA
Stel dat we willen bepalen of drie verschillende studiemethoden tot verschillende gemiddelde examenscores leiden. Om dit te testen, rekruteren we 30 studenten en wijzen we er willekeurig 10 toe om een andere studiemethode te gebruiken.
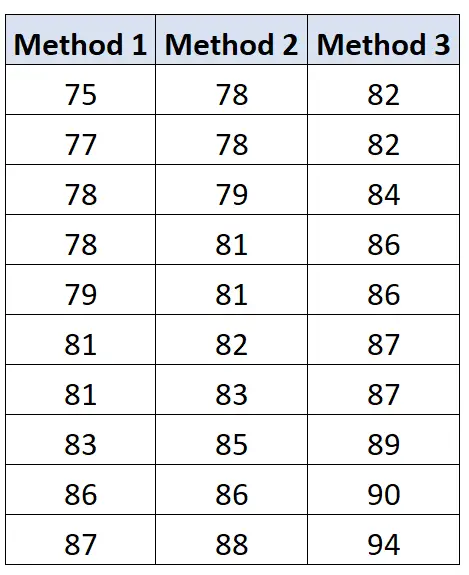
Hieronder vindt u de examenresultaten van studenten per groep:
We kunnen de volgende formule gebruiken om de variatie tussen groepen te berekenen:
Variatie tussen groepen = Σn j (X j – X ..) 2
Goud:
- n j : de steekproefomvang van groep j
- Σ : een symbool dat “som” betekent
- Xj : het gemiddelde van groep j
- X .. : het algemene gemiddelde
Om deze waarde te berekenen, berekenen we eerst het gemiddelde van elke groep en het algemene gemiddelde:
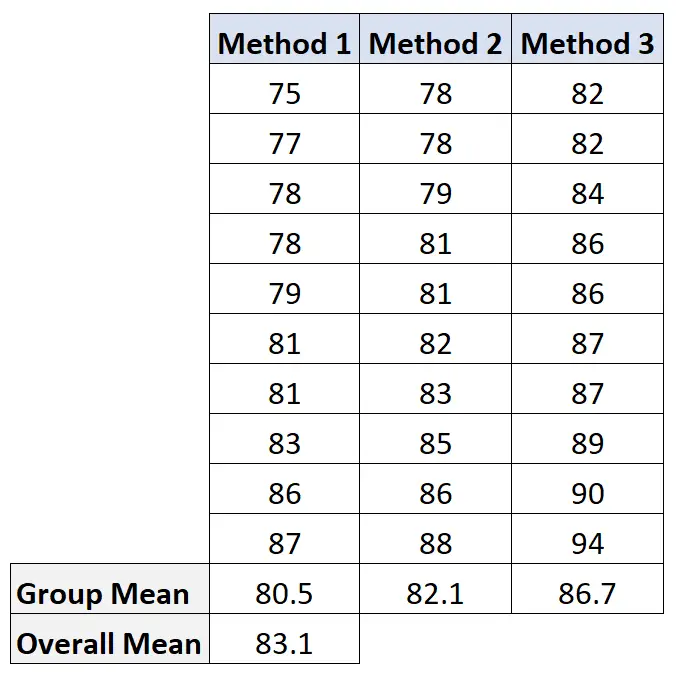
Vervolgens berekenen we de variatie tussen groepen als volgt: 10(80,5-83,1) 2 + 10(82,1-83,1) 2 + 10(86,7-83,1) 2 = 207,2 .
Vervolgens kunnen we de volgende formule gebruiken om de variatie binnen de groep te berekenen:
Variatie binnen de groep : Σ(X ij – X j ) 2
Goud:
- Σ : een symbool dat “som” betekent
- X ij : de ide waarneming van groep j
- Xj : het gemiddelde van groep j
In ons voorbeeld berekenen we de variatie binnen de groep als:
Groep 1: (75-80,5) 2 + (77-80,5) 2 + (78-80,5) 2+ (78-80,5) 2+ (79-80,5) 2+ (81-80,5) 2+ (81-80,5) 2+ (83-80,5) 2+ (86-80,5) 2+ (87-80,5) 2 = 136,5
Groep 2: (78-82.1) 2 + (78-82.1) 2 + (79-82,1) 2+ (81-82,1) 2+ (81-82,1) 2+ (82-82,1) 2+ (83-82,1) 2+ (85-82,1) 2+ (86-82,1) 2+ (88-82,1) 2 = 104,9
Groep 3: (82-86,7) 2 + (82-86,7) 2 + (84-86,7) 2+ (86-86,7) 2+ (86-86,7) 2+ (87-86,7) 2+ (87-86,7) 2+ (89-86,7) 2+ (90-86,7) 2+ (94-86,7) 2 = 122,1
Variatie binnen groep: 136,5 + 104,9 + 122,1 = 363,5
Als we statistische software gebruiken om een one-way ANOVA uit te voeren met behulp van deze dataset, krijgen we de volgende ANOVA-tabel:
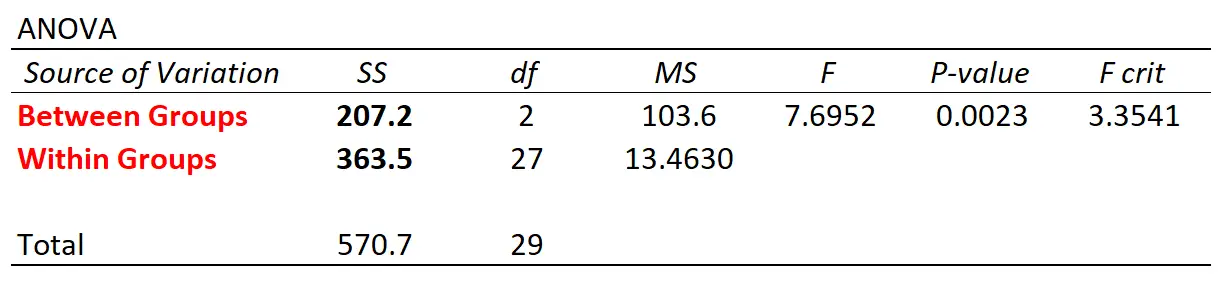
Merk op dat de variatiewaarden tussen en binnen de groep overeenkomen met de waarden die we handmatig hebben berekend.
De algemene F-statistiek in de tabel is een manier om de relatie tussen variatie tussen groepen en variatie binnen de groep te kwantificeren.
Hoe groter de F-statistiek, hoe groter de variatie tussen groepen betekent ten opzichte van de variatie binnen groepen.
Dus hoe groter de F-statistiek, hoe duidelijker het is dat er een verschil is tussen de groepsgemiddelden.
We kunnen in dit voorbeeld zien dat de p-waarde die overeenkomt met een F-statistiek van 7,6952 .0023 is.
Omdat deze waarde kleiner is dan α = 0,05 verwerpen we de nulhypothese van de ANOVA en concluderen we dat de drie studietechnieken niet tot dezelfde score op het examen leiden.
Aanvullende bronnen
De volgende tutorials bieden aanvullende informatie over ANOVA-modellen:
Inleiding tot One-Way ANOVA
Hoe F-waarde en P-waarde in ANOVA te interpreteren
De complete gids: ANOVA-resultaten rapporteren
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder