Quasivariantie

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat quasivariantie in de statistiek is. Zo ontdek je hoe je de quasivariantie berekent, een opgeloste oefening en wat de verschillen zijn tussen de quasivariantie en de variantie. Bovendien kunt u de quasivariantie van elke dataset berekenen met een online rekenmachine.

Wat is quasivariantie?

In de statistiek is quasivariantie een maatstaf voor de spreiding die de variabiliteit van een steekproef aangeeft. Nauwkeuriger gezegd, de quasivariantie is gelijk aan de som van de kwadraten van de afwijkingen gedeeld door het totale aantal waarnemingen min één.

Het symbool voor quasivariantie is

$\sigma_{n-1}^2$

$s_{n-1}^2$

. soms Hoewel het symbool ook wordt gebruikt

$\widehat{s}^2$

om de quasivariantie weer te geven.

Quasivariantie wordt gebruikt om de spreiding van een steekproef te bepalen en vertekening te vermijden. Daarom wordt het vaak onbevooroordeelde variantie genoemd. De quasivariantie is daarom een goede schatter van de populatievariantie. Bij het berekenen van de steekproefvariantie wordt vaak de quasi-variantieformule gebruikt in plaats van de variantieformule. Hieronder gaan we dieper in op het verschil tussen deze twee statistische metingen.

Quasivariantie-formule

Om de quasivariantie te berekenen, moet men de som van de kwadraten van de verschillen tussen de waarden en het gemiddelde van de dataset vinden en deze later delen door het totale aantal gegevens min één.

De formule om de quasivariantie te berekenen is dus als volgt:

Goud:

$\sigma_{n-1}^2$

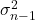
is de quasivariantie.
$x_i$

is de gegevenswaarde

$i$

.
$n$

is het totale aantal gegevens.
$\overline{X}$

is het gemiddelde van de dataset.

👉 U kunt de onderstaande rekenmachine gebruiken om de quasivariantie van elke dataset te berekenen.

Je vraagt je misschien af waarom het wordt gedeeld door n-1 en niet door n? Het gaat erom de vertekening te elimineren, op deze manier krijgen we een zuivere schatter. Dit is precies de reden waarom quasivariantie een goede schatter is van populatievariantie.

Voorbeeld van quasivariantieberekening

Nu we de definitie van quasivariantie kennen, zullen we een eenvoudig voorbeeld oplossen, zodat u kunt zien hoe de quasivariantie van een gegevensreeks wordt berekend.

Van een multinationale onderneming kennen we het economische resultaat dat het de afgelopen vijf jaar heeft behaald; het merendeel behaalde winst, maar een jaar lang boekte het aanzienlijke verliezen: 11,5, 2, -9, 7 miljoen euro. Bereken de quasivariantie van deze dataset.

Het eerste dat we moeten doen om de quasivariantie van een dataset te bepalen, is het rekenkundig gemiddelde ervan berekenen:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

En zodra we de gemiddelde waarde van de gegevens kennen, passen we de quasivariantieformule toe:

$\sigma_{n-1}^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

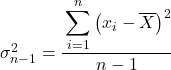
We vervangen dus de gegevens uit de oefeninstructie in de formule:

$\sigma_{n-1}^2=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5-1}$

Ten slotte is het voldoende om de bewerkingen op te lossen om de quasivariantie te berekenen:

$\begin{aligned}\sigma_{n-1}^2&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5-1}\\[2ex]&= \cfrac{228,8}{4} \\[2ex]&=57,2 \ \text{millones de euros}^2\end{aligned}$

Merk op dat de eenheden van de quasivariantie dezelfde eenheden zijn als de eenheden van de statistische gegevens, maar dan in het kwadraat, dus de quasivariantie van deze dataset is 57,2 miljoen ² .

➤ Zie: Quasi-standaarddeviatie

Quasivariantie rekenmachine

Voer een statistische gegevensset in de volgende rekenmachine in om de quasivariantie ervan te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Variantie en quasivariantie

Ten slotte zullen we het verschil zien tussen quasivariantie en variantie, omdat ze ondanks hun gelijkenis in naam ook zeer vergelijkbaar worden berekend.

Het verschil tussen de quasivariantie en de variantie is de noemer van de formule. Om de quasivariantie te berekenen, moet u delen door n-1. De variantie wordt echter berekend door te delen door n.

Quasivariantie en variantie zijn dus wiskundig gerelateerd, aangezien quasivariantie equivalent is aan variantie vermenigvuldigd met n (het totale aantal datapunten) en gedeeld door n-1.

$\sigma_{n-1}^2=\cfrac{n}{n-1}\cdot \sigma^2$

Daarom zal voor dezelfde gegevensset de quasivariantiewaarde altijd groter zijn dan de variantiewaarde.

➤ Zie: Eigenschappen van afwijkingen

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder