Hoe u eenvoudige lineaire regressie uitvoert in sas

Eenvoudige lineaire regressie is een techniek die we kunnen gebruiken om de relatie tussen een voorspellende variabele en een responsvariabele te begrijpen.

Deze techniek vindt een lijn die het beste bij de gegevens past en neemt de volgende vorm aan:

ŷ = _b0 + _b1 x

Goud:

• ŷ : De geschatte responswaarde
• b ₀ : De oorsprong van de regressielijn
• b ₁ : De helling van de regressielijn

Deze vergelijking helpt ons de relatie tussen de voorspellende variabele en de responsvariabele te begrijpen.

In het volgende stapsgewijze voorbeeld ziet u hoe u een eenvoudige lineaire regressie in SAS uitvoert.

Stap 1: Creëer de gegevens

Voor dit voorbeeld maken we een dataset aan met daarin het totaal aantal gestudeerde uren en het eindexamencijfer van 15 studenten.

We passen een eenvoudig lineair regressiemodel toe met uren als voorspellende variabele en score als responsvariabele.

De volgende code laat zien hoe u deze gegevensset in SAS maakt:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

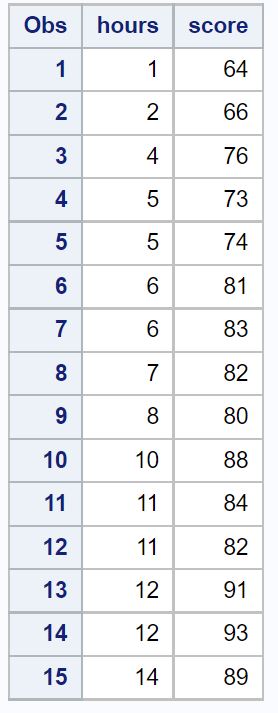
Stap 2: Pas het eenvoudige lineaire regressiemodel toe

Vervolgens zullen we proc reg gebruiken om in het eenvoudige lineaire regressiemodel te passen:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

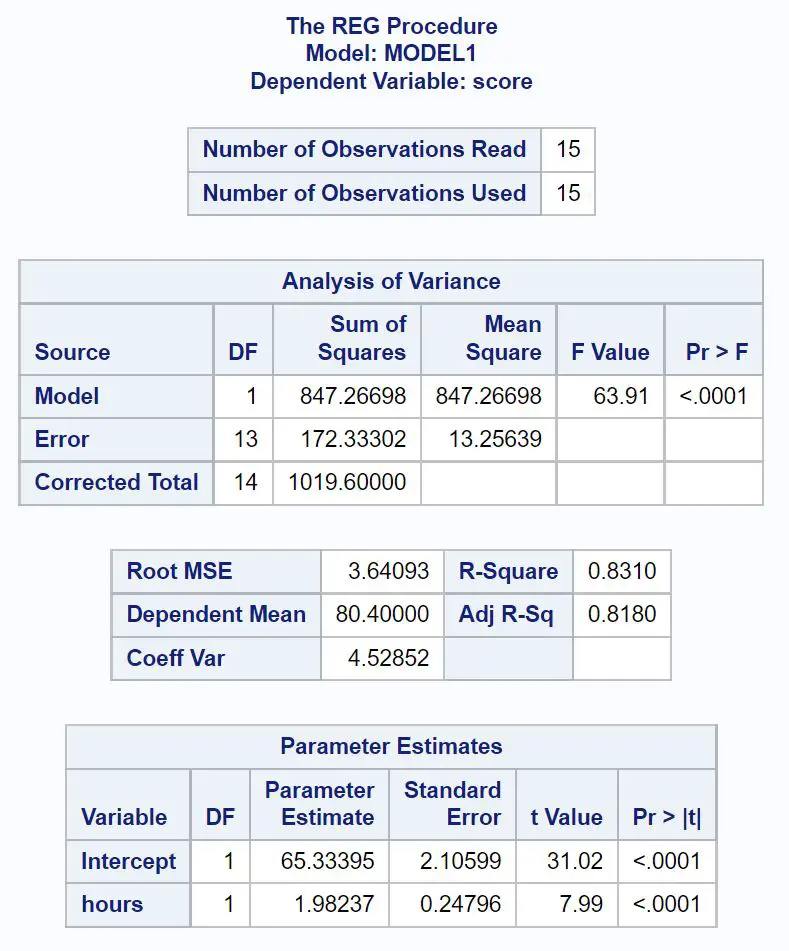
Zo interpreteert u de belangrijkste waarden uit elke tabel in het resultaat:

Tabel met gap-analyse:

De totale F-waarde van het regressiemodel is 63,91 en de overeenkomstige p-waarde is <0,0001 .

Omdat deze p-waarde kleiner is dan 0,05 concluderen we dat het regressiemodel als geheel statistisch significant is. Met andere woorden: uren zijn een nuttige variabele voor het voorspellen van examenresultaten.

Model passende tafel:

De R-Square-waarde vertelt ons het percentage variatie in examenscores dat kan worden verklaard door het aantal bestudeerde uren.

Over het algemeen geldt dat hoe groter de R-kwadraatwaarde van een regressiemodel is, hoe beter de voorspellende variabelen de waarde van de responsvariabele kunnen voorspellen.

In dit geval kan 83,1% van de variatie in examenscores worden verklaard door het aantal gestudeerde uren. Deze waarde is vrij hoog, wat aangeeft dat het aantal gestudeerde uren een zeer nuttige variabele is bij het voorspellen van examenresultaten.

Tabel met parameterschattingen:

Uit deze tabel kunnen we de gepaste regressievergelijking zien:

Score = 65,33 + 1,98*(uur)

Wij interpreteren dit zo dat elk extra uur dat je studeerde gepaard gaat met een gemiddelde stijging van 1,98 punten in de examenscore.

De oorspronkelijke waarde vertelt ons dat de gemiddelde examenscore voor een student die nul uur studeert 65,33 is.

We kunnen deze vergelijking ook gebruiken om de verwachte examenscore te vinden op basis van het aantal uren dat een student studeert.

Een student die bijvoorbeeld 10 uur studeert, moet een examenscore van 85,13 behalen:

Score = 65,33 + 1,98*(10) = 85,13

Omdat de p-waarde (<0,0001) voor uren in deze tabel kleiner is dan 0,05, concluderen we dat dit een statistisch significante voorspellende variabele is.

Stap 3: Analyseer restpercelen

Eenvoudige lineaire regressie maakt twee belangrijke aannames over de modelresiduen :

• De residuen zijn normaal verdeeld.
• De residuen hebben een gelijke variantie (“ homoscedasticiteit ”) op elk niveau van de voorspellende variabele.

Als niet aan deze aannames wordt voldaan, zijn de resultaten van ons regressiemodel mogelijk niet betrouwbaar.

Om te verifiëren dat aan deze aannames wordt voldaan, kunnen we de resterende plots analyseren die SAS automatisch in de uitvoer weergeeft:

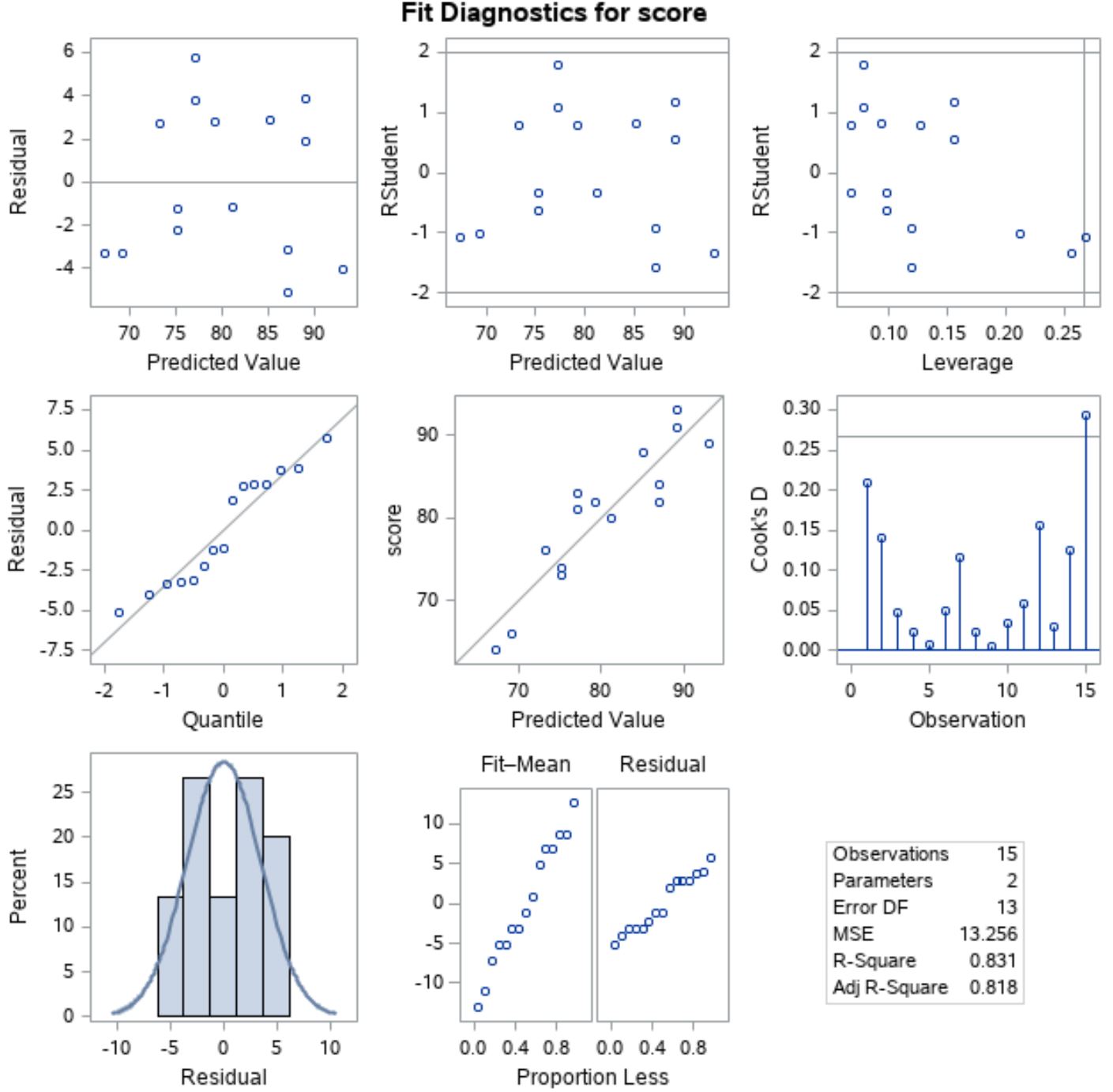
Om te verifiëren dat de residuen normaal verdeeld zijn, kunnen we de grafiek op de linkerpositie van de middelste lijn analyseren met „Kwantiel“ langs de x-as en „Residuaal“ langs de y-as.

Deze plot wordteen QQ-plot genoemd, een afkorting van „quantile-quantile“, en wordt gebruikt om te bepalen of de gegevens normaal verdeeld zijn of niet. Als de gegevens normaal verdeeld zijn, liggen de punten op een QQ-plot op een rechte diagonale lijn.

Uit de grafiek kunnen we zien dat de punten grofweg langs een rechte diagonale lijn liggen, dus we kunnen aannemen dat de residuen normaal verdeeld zijn.

Om vervolgens te verifiëren dat de residuen homoscedastisch zijn, kunnen we naar de grafiek op de linkerpositie van de eerste rij kijken met „Voorspelde waarde“ langs de x-as en „Residuaal“ langs de y-as.

Als de plotpunten willekeurig rond nul verspreid zijn zonder duidelijk patroon, kunnen we aannemen dat de residuen homoskedastisch zijn.

Uit de plot kunnen we zien dat de punten willekeurig rond nul verspreid zijn met ongeveer gelijke variantie op elk niveau in de plot, dus we kunnen aannemen dat de residuen homoscedastisch zijn.

Omdat aan beide aannames wordt voldaan, kunnen we aannemen dat de resultaten van het eenvoudige lineaire regressiemodel betrouwbaar zijn.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Eenrichtings-ANOVA uitvoeren in SAS
Hoe u tweerichtings-ANOVA uitvoert in SAS
Hoe de correlatie in SAS te berekenen