Steekproefverdeling van het gemiddelde

In dit artikel wordt uitgelegd wat de steekproefverdeling van het gemiddelde in de statistiek is. U vindt er ook de formule voor de gemiddelde steekproefverdeling en een stapsgewijze op te lossen oefening.

Wat is de steekproefverdeling van het gemiddelde?

De steekproefverdeling van het gemiddelde (of steekproefverdeling van gemiddelden ) is de verdeling die voortvloeit uit de berekening van het steekproefgemiddelde van elke mogelijke steekproef uit een populatie. Dat wil zeggen dat de verzameling steekproefgemiddelden uit alle mogelijke steekproeven uit een populatie de steekproefverdeling van het gemiddelde vormt.

Of met andere woorden: als we alle steekproeven bestuderen die uit een populatie kunnen worden genomen en het gemiddelde van elk van de steekproeven berekenen, vormt de reeks berekende waarden een steekproefverdeling van het steekproefgemiddelde.

In de statistiek wordt de steekproefverdeling van het gemiddelde gebruikt om de waarschijnlijkheid te berekenen dat de waarde van het populatiegemiddelde wordt benaderd bij het analyseren van een enkele steekproef.

Formule voor de steekproefverdeling van het gemiddelde

Gegeven een populatie die een normale kansverdeling met gemiddelde volgt

en standaarddeviatie

en er worden maatmonsters genomen

, zal de steekproefverdeling van het gemiddelde ook worden gedefinieerd door een normale verdeling met de volgende kenmerken:

Goud

is het gemiddelde van de steekproefverdeling van het gemiddelde en

is de standaarddeviatie. Verder,

is de standaardfout van de steekproefverdeling.

Opmerking: Als de populatie geen normale verdeling volgt, maar de steekproefomvang groot is (n>30), kan de steekproefverdeling van het gemiddelde ook worden benaderd met de vorige normale verdeling door de centrale limietstelling.

Omdat de steekproefverdeling van het gemiddelde een normale verdeling volgt, is de formule voor het berekenen van elke waarschijnlijkheid gerelateerd aan het steekproefgemiddelde daarom:

Goud:

• 

  is het steekproefgemiddelde.

• 

  Dit is het bevolkingsgemiddelde.

• 

  is de standaarddeviatie van de populatie.

• 

  is de steekproefomvang.

• 

  is een variabele gedefinieerd door de standaard normale verdeling N(0,1).

Voorbeeld uit de praktijk van de steekproefverdeling van het gemiddelde

Nadat we de definitie van de steekproefverdeling van het gemiddelde hebben gezien en wat de bijbehorende formules zijn, gaan we een voorbeeld oplossen om het concept beter te begrijpen.

• Het gewicht van universiteitsstudenten volgt een normale verdeling met een gemiddelde van 68 kg en een standaarddeviatie van 9 kg. Bepaald:
  1. Wat is de kans dat het gemiddelde van een willekeurige steekproef van 25 studenten minder dan 66 kg weegt?
  2. Als er 300 monsters worden genomen met een grootte van elk 25 studenten, hoeveel monstergemiddelden zullen dan een waarde hebben van minder dan 66 kg?

Allereerst moeten we de waarde van de overeenkomstige statistiek berekenen, hiervoor passen we de formule toe die we hierboven zagen:

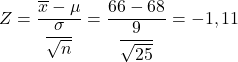
De waarschijnlijkheid waarnaar we op zoek zijn, is daarom de waarschijnlijkheid die overeenkomt met de waarde Z=-1,11 van de linkerstaart van de standaardnormale verdeling, die gemakkelijk kan worden verkregen uit de Z-waarschijnlijkheidstabel. We gebruiken daarom de Z-tabel om de waarschijnlijkheid te bepalen die het probleem ons vraagt:

Nu we de waarschijnlijkheid kennen dat het gemiddelde van een willekeurige steekproef minder is dan 66 kg, moeten we, om te weten dat het aantal monsters minder dan 66 kg betekent bij 300 gelijke monsters, de berekende waarschijnlijkheid vermenigvuldigen met het totale aantal genomen monsters:

Daarom zullen ongeveer 40 van de getrokken monsters gemiddeld minder dan 66 kg wegen.