Hypothesetesten voor verschil in gemiddelden

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat het testen van verschil-van-gemiddelde-hypothesen in de statistiek is en waarvoor het wordt gebruikt. Op dezelfde manier zul je ontdekken hoe je een hypothesetest kunt doen over het verschil in gemiddelden en een stapsgewijze opgeloste oefening.

Wat is het testen van hypothesen voor gemiddelde verschillen?

Hypothesetesten voor verschil in gemiddelden zijn een statistische test die wordt gebruikt om de hypothese dat de gemiddelden van twee populaties verschillend zijn, te verwerpen of te accepteren. Dat wil zeggen dat de verschil-in-gemiddelden-hypothesetest wordt gebruikt om te bepalen of de gemiddelden van twee populaties hetzelfde of verschillend zijn.

Houd er rekening mee dat beslissingen die bij het testen van hypothesen worden genomen, gebaseerd zijn op een eerder vastgesteld niveau van vertrouwen . Je kunt dus niet garanderen dat het resultaat van een hypothesetest altijd correct is, maar dat dit de meest waarschijnlijke uitkomst is die waar is.

Het testen van hypothesen voor het verschil tussen twee gemiddelden omvat het berekenen van de teststatistiek en het vergelijken ervan met de kritische waarde om de nulhypothese al dan niet te verwerpen. Hieronder zullen we zien hoe u een hypothesetest kunt uitvoeren voor het verschil in gemiddelden.

Bedenk ten slotte dat het testen van hypothesen in de statistiek ook hypothesecontrasten, hypothesetesten of significantietesten kan worden genoemd.

➤ Zie: Steekproefverdeling van verschil in gemiddelden

Hypothesetestformule voor verschil in gemiddelden

De formule die moet worden gebruikt om hypothesen over het verschil in gemiddelden te testen, varieert afhankelijk van het feit of de populatievarianties bekend zijn en, zo niet, of kan worden aangenomen dat ze hetzelfde of verschillend zijn. In dit gedeelte zullen we dus zien welke formule we moeten gebruiken, afhankelijk van het geval.

Bekende variaties

De formule voor het berekenen van de hypotheseteststatistiek voor het verschil in gemiddelden wanneer de varianties bekend zijn, is als volgt:

$\displaystyle Z=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Goud:

$Z$

is de hypotheseteststatistiek voor het verschil tussen twee gemiddelden met bekende variantie, die een standaard normale verdeling volgt.
$\mu_1$

is het gemiddelde van populatie 1.
$\mu_2$

is het gemiddelde van populatie 2.
$\overline{x_1}$

is het gemiddelde van monster 1.
$\overline{x_2}$

is het gemiddelde van monster 2.
$\sigma_1$

is de standaardafwijking van populatie 1.
$\sigma_2$

is de standaardafwijking van populatie 2.
$n_1$

is steekproefomvang 1.
$n_2$

is steekproefomvang 2.

Houd er rekening mee dat dit het minst voorkomende geval is, dus deze formule wordt alleen in bepaalde specifieke gevallen gebruikt.

Onbekende en gelijke afwijkingen

De formule voor het berekenen van de hypotheseteststatistiek voor het verschil in gemiddelden wanneer de populatievarianties onbekend zijn maar verondersteld wordt gelijk te zijn, is:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Goud:

$t$

is de hypotheseteststatistiek voor het verschil in gemiddelden met onbekende varianties, die een Student’s t-verdeling volgt met n ₁ + n ₂ -2 vrijheidsgraden.
$\mu_1$

is het gemiddelde van populatie 1.
$\mu_2$

is het gemiddelde van populatie 2.
$\overline{x_1}$

is het gemiddelde van monster 1.
$\overline{x_2}$

is het gemiddelde van monster 2.
$s_p$

is de gecombineerde standaarddeviatie.
$n_1$

is steekproefomvang 1.
$n_2$

is steekproefomvang 2.

De gecombineerde standaardafwijking van de twee monsters wordt berekend met de volgende formule:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Onbekende en verschillende varianten

Wanneer de populatievarianties onbekend zijn en bovendien wordt aangenomen dat ze verschillend zijn, is de formule voor het berekenen van de hypothesetoetsingsstatistiek voor het verschil in gemiddelden als volgt:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Goud:

$t$

is de hypotheseteststatistiek voor het verschil in gemiddelden met onbekende varianties, die de Student’s t-verdeling volgt.
$\mu_1$

is het gemiddelde van populatie 1.
$\mu_2$

is het gemiddelde van populatie 2.
$\overline{x_1}$

is het gemiddelde van monster 1.
$\overline{x_2}$

is het gemiddelde van monster 2.
$\sigma_1$

is de standaardafwijking van populatie 1.
$\sigma_2$

is de standaardafwijking van populatie 2.
$n_1$

is steekproefomvang 1.
$n_2$

is steekproefomvang 2.

In dit geval worden de vrijheidsgraden van de Student’s t-verdeling echter berekend met behulp van de volgende formule:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Zie: Betrouwbaarheidsintervalformule voor verschil in gemiddelden

Concreet voorbeeld van het testen van hypothesen voor het verschil in gemiddelden

Om het concept van het testen van hypothesen op het verschil in gemiddelden af te ronden, zullen we een concreet voorbeeld zien van dit soort hypothesetesten.

U wilt een statistisch onderzoek doen naar de salarissen van twee concurrerende bedrijven, meer specifiek wilt u bepalen of het gemiddelde salaris van de twee bedrijven verschillend is. Om dit te doen, wordt een steekproef van 47 werknemers van het ene bedrijf en een andere steekproef van 55 werknemers van het andere bedrijf genomen. Uit de eerste steekproef wordt een gemiddeld salaris van $40.000 en een standaardafwijking van $12.000 verkregen, terwijl uit de tweede steekproef een gemiddeld salaris van $46.000 en een standaardafwijking van $18.000 wordt verkregen. Voer een hypothesetest uit met een significantieniveau van 5% om te bepalen of de gemiddelde salarissen verschillend zijn of niet.

In dit geval zijn de nulhypothese en de alternatieve hypothese van de hypothesetest voor het verschil tussen de twee gemiddelden als volgt:

$\begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}$

In dit geval zijn de bevolkingskloven niet bekend, maar kan worden aangenomen dat ze gelijk zijn omdat het concurrerende bedrijven zijn en de arbeidsomstandigheden op de markt waarin ze opereren zeer vergelijkbaar zijn. Daarom is de formule voor de hypotheseteststatistiek voor het verschil in gemiddelden die we moeten gebruiken:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

We berekenen daarom de gepoolde standaardafwijking van de twee steekproeven:

$\begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}$

We passen nu de formule voor het testen van de hypothese toe voor het verschil in gemiddelden:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\cfrac{(40000-46000)-0}{\displaystyle 15530,61\sqrt{\frac{1}{47}+\frac{1}{55}}}=-1,94$

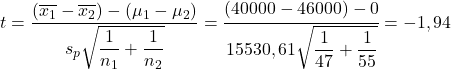
Aan de andere kant zoeken we naar de kritische waarde van de hypothesetest voor het verschil in gemiddelden in de Student’s t-tabel :

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}$

Omdat de absolute waarde van de teststatistiek kleiner is dan de kritische testwaarde, wordt vervolgens de nulhypothese geaccepteerd en de alternatieve hypothese verworpen.

$|-1,94|=1,94<1,984 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Wat is het testen van hypothesen voor gemiddelde verschillen?

Hypothesetestformule voor verschil in gemiddelden

Bekende variaties

Onbekende en gelijke afwijkingen

Onbekende en verschillende varianten

Concreet voorbeeld van het testen van hypothesen voor het verschil in gemiddelden

Über den Autor

Dr.benjamin anderson

Einen Kommentar hinzufügen