Bemonsteringsverdeling

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de steekproefverdeling in de statistiek is en waarvoor deze wordt gebruikt. Zo vind je de betekenis van een steekproevenverdeling, een concreet voorbeeld van een steekproevenverdeling en daarnaast de formules voor de meest voorkomende soorten steekproevenverdelingen.

Wat is de steekproefverdeling?

De steekproevenverdeling , of steekproevenverdeling , is de verdeling die het resultaat is van het in overweging nemen van alle mogelijke steekproeven uit een populatie. Met andere woorden: de steekproefverdeling is de verdeling die wordt verkregen door het berekenen van een steekproefparameter van alle mogelijke steekproeven uit een populatie.

Als we bijvoorbeeld alle mogelijke steekproeven uit een statistische populatie extraheren en het gemiddelde van elke steekproef berekenen, vormt de verzameling steekproefgemiddelden een steekproefverdeling. Preciezer gezegd: aangezien de berekende parameter het rekenkundig gemiddelde is, is dit de steekproefverdeling van het gemiddelde.

In de statistiek wordt de steekproefverdeling gebruikt om de waarschijnlijkheid te berekenen dat de waarde van de populatieparameter wordt benaderd bij het bestuderen van een enkele steekproef. Op dezelfde manier stelt de steekproefverdeling ons in staat de steekproeffout voor een gegeven steekproefomvang te schatten.

Voorbeeld van bemonsteringsverdeling

Nu we de definitie van steekproevenverdeling kennen, kunnen we naar een eenvoudig voorbeeld kijken om het concept volledig te begrijpen.

In een doos stoppen we drie ballen en op elke bal staat een nummer geschreven van één tot drie, zodat de ene bal het nummer 1 heeft, de andere bal het nummer 2 en de laatste bal het nummer 3 heeft. Voor een monster van grootte n = 2, berekent de waarschijnlijkheid van de steekproefverdeling van het gemiddelde als monsters met vervanging worden geselecteerd.

Monsters worden geselecteerd met vervanging, dat wil zeggen dat de bal die is opgepakt om het eerste element van het monster te selecteren, terug in de doos wordt geplaatst en tijdens de tweede extractie opnieuw kan worden geselecteerd. Daarom zijn alle mogelijke steekproeven uit de populatie:

1,1 1,2 1,3
2.1 2.2 2.3
3.1 3.2 3.3

We berekenen dus het rekenkundig gemiddelde van elk mogelijk monster:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

Daarom zijn de kansen om elke waarde van het steekproefgemiddelde te verkrijgen bij het selecteren van een willekeurige steekproef uit de populatie als volgt:

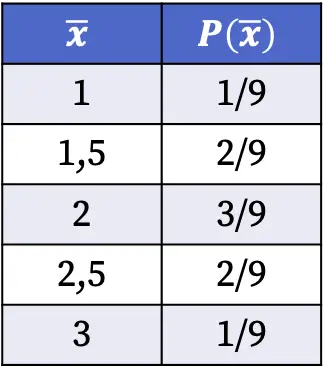
De kansen op de steekproevenverdeling, weergegeven in de bovenstaande tabel, werden berekend door het aantal monsters met de genoemde gemiddelde waarde te delen door het totale aantal mogelijke gevallen. Bijvoorbeeld: het steekproefgemiddelde is in twee van de negen mogelijke gevallen 1,5, dus P(1,5)=2/9.

Soorten steekproefverdelingen

Steekproefverdelingen (of steekproevenverdelingen) kunnen worden geclassificeerd op basis van de steekproefparameter waaruit ze zijn verkregen. De meest voorkomende soorten distributies zijn dus als volgt:

Steekproefverdeling van het gemiddelde : Dit is de steekproefverdeling die het resultaat is van de berekening van het rekenkundig gemiddelde van elke steekproef.
Proportiebemonsteringsverdeling : Het is de steekproefverdeling die wordt verkregen door het aandeel van alle monsters te berekenen.
Steekproefverdeling van variantie : Dit is de steekproefverdeling die de verzameling van alle varianties in de steekproef vormt.
Verschil in steekproefverdeling : is de steekproefverdeling die het resultaat is van de berekening van het verschil tussen de gemiddelden van alle mogelijke steekproeven uit twee verschillende populaties.
Verschil in verhoudingen Steekproefverdeling : is de steekproefverdeling die wordt verkregen door alle mogelijke steekproefverhoudingen van twee populaties af te trekken.

Hieronder wordt elk type steekproefverdeling nader toegelicht.

Steekproefverdeling van het gemiddelde

Gegeven een populatie die een normale kansverdeling met gemiddelde volgt

$\mu$

en standaarddeviatie

$\sigma$

en maatmonsters worden geëxtraheerd

$n$

, zal de steekproefverdeling van het gemiddelde ook worden gedefinieerd door een normale verdeling met de volgende kenmerken:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Goud

$\mu_{\overline{x}}$

is het gemiddelde van de steekproefverdeling van het gemiddelde en

$\sigma_{\overline{x}}$

is de standaarddeviatie. Verder,

$\cfrac{\sigma}{\sqrt{n}}$

is de standaardfout van de steekproefverdeling.

Opmerking: Als de populatie geen normale verdeling volgt, maar de steekproefomvang groot is (n>30), kan de steekproefverdeling van het gemiddelde ook worden benaderd tot de normale verdeling hierboven door de limiet van de centrale stelling.

Omdat de steekproefverdeling van het gemiddelde een normale verdeling volgt, is de formule voor het berekenen van elke waarschijnlijkheid gerelateerd aan het steekproefgemiddelde daarom:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Goud:

$\overline{x}$

is het steekproefgemiddelde.
$\mu$

Dit is het populatiegemiddelde.
$s$

is de standaarddeviatie van de populatie.
$n$

is de steekproefomvang.
$Z$

is een variabele gedefinieerd door de standaard normale verdeling N(0,1).

➤ Zie: Opgeloste oefening over de steekproefverdeling van het gemiddelde

Bemonsteringsverdeling van proporties

Wanneer we een deel van een steekproef bestuderen, analyseren we in feite succesgevallen. Daarom volgt de willekeurige variabele in het onderzoek een binomiale waarschijnlijkheidsverdeling.

Volgens de centrale limietstelling kunnen we voor grote maten (n>30) een binomiale verdeling dichter bij een normale verdeling brengen. Daarom benadert de steekproefverdeling van het aandeel een normale verdeling met de volgende parameters:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Goud

$p$

is de kans op succes en

$q$

is de kans op falen

$q=1-p$

Opmerking: een binominale verdeling kan alleen worden benaderd als een normale verdeling als:

$n>30″ title=“Rendered by QuickLaTeX.com“ height=“14″ width=“52″ style=“vertical-align: -2px;“></p> <p> ,</p> <p class=$ $np\ge 5$

$nq\ge 5$

Omdat de steekproefverdeling van het aandeel kan worden benaderd tot een normale verdeling, is de formule voor het berekenen van elke waarschijnlijkheid die verband houdt met het aandeel van een steekproef daarom:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Goud:

$\widehat{p}$

is de steekproefaandeel.
$p$

is het aandeel van de bevolking.
$q$

is de kans op falen van de populatie,

$q=1-p$

.
$n$

is de steekproefomvang.
$Z$

is een variabele gedefinieerd door de standaard normale verdeling N(0,1).

➤ Zie: Opgeloste oefening over de steekproevenverdeling van het aandeel

Bemonsteringsverdeling van variantie

De steekproefvariantieverdeling wordt gedefinieerd door de chikwadraat-kansverdeling. Daarom is de formule voor de statistiek van de steekproefvariantieverdeling :

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Goud:

$\chi^2$

is de statistiek van de steekproefvariantieverdeling, die een chikwadraatverdeling volgt.
$n$

is de steekproefomvang.
$s^2$

is de steekproefvariantie.
$\sigma^2$

is de populatievariantie.

➤ Zie: Opgeloste oefening over de steekproefverdeling van variantie

Steekproefverdeling van verschil in gemiddelden

Als de steekproefomvang groot genoeg is (n ₁ ≥30 en n ₂ ≥30), volgt de steekproefverdeling van het gemiddelde verschil een normale verdeling. Meer precies worden de parameters van genoemde verdeling als volgt berekend:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Opmerking: Als beide populaties normale verdelingen zijn, volgt de steekproefverdeling van het verschil in gemiddelden een normale verdeling, ongeacht de steekproefomvang.

Omdat de steekproefverdeling van het verschil in gemiddelden wordt gedefinieerd door een normale verdeling, is de formule voor het berekenen van de statistiek van de steekproefverdeling van het verschil in gemiddelden daarom:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Goud:

$\overline{x_i}$

is het gemiddelde van monster i.
$\mu_i$

is het gemiddelde van de populatie i.
$\sigma_i$

is de standaardafwijking van populatie i.
$n_i$

is de steekproefomvang i.
$Z$

is een variabele gedefinieerd door de standaard normale verdeling N(0,1).

Houd er rekening mee dat steekproeven uit verschillende populaties verschillende steekproefgroottes kunnen hebben.

➤ Zie: Opgeloste oefening over de steekproevenverdeling van het verschil in gemiddelden

Bemonsteringsverdeling van verschil in verhoudingen

De steekproeven die zijn geselecteerd op basis van het verschil in proporties van de steekproevenverdeling worden gedefinieerd door binomiale verdelingen, omdat voor praktische doeleinden een proportie de verhouding is tussen succesgevallen en het totale aantal waarnemingen.

Vanwege de centrale limietstelling kunnen binominale verdelingen echter worden benaderd als normale waarschijnlijkheidsverdelingen. Daarom kan de steekproefverdeling van het verschil in verhoudingen worden benaderd tot een normale verdeling met de volgende kenmerken:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Opmerking: De steekproefverdeling van het verschil in verhoudingen kan alleen worden benaderd als een normale verdeling als:

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

$n_2q_2\geq5$

Omdat de steekproefverdeling van het verschil in verhoudingen kan worden benaderd tot een normale verdeling, is de formule voor het berekenen van de statistiek van de steekproefverdeling van het verschil in verhoudingen daarom als volgt:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

Goud:

$\widehat{p_i}$

is de steekproefaandeel i.
$p_i$

is het aandeel van de bevolking i.
$q_i$

is de kans op falen van populatie i,

$q_i=1-p_i$

.
$n_i$

is de steekproefomvang i.
$Z$

is een variabele gedefinieerd door de standaard normale verdeling N(0,1).

➤ Zie: Opgeloste oefening over de steekproevenverdeling van het verschil in verhoudingen

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Wat is de steekproefverdeling?

Voorbeeld van bemonsteringsverdeling

Soorten steekproefverdelingen

Steekproefverdeling van het gemiddelde

Bemonsteringsverdeling van proporties

Bemonsteringsverdeling van variantie

Steekproefverdeling van verschil in gemiddelden

Bemonsteringsverdeling van verschil in verhoudingen

Über den Autor

Dr.benjamin anderson

Einen Kommentar hinzufügen