Student's t-test

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de Student t-toets is en waarvoor deze in de statistiek wordt gebruikt. Zo zul je ontdekken hoe de Student’s t-test wordt uitgevoerd, wat de verschillende soorten Student’s t-tests zijn en de formule voor elke test.

Wat is de Student’s t-toets?

De Student’s t-test , ook wel de T-test of eenvoudigweg t-test genoemd, is een statistische test waarbij de teststatistiek de t-verdeling van de Student volgt. Daarom wordt in de statistiek de Student’s t-test gebruikt om de nulhypothese van een hypothesetest te verwerpen of te accepteren.

Concreet wordt de Student’s t-test gebruikt bij het testen van hypothesen waarbij de bestudeerde populatie een normale verdeling volgt, maar de steekproefomvang te klein is om de populatievariantie te kennen.

Kortom, Student’s t-test wordt gebruikt om de studiehypothese van bepaalde hypothesetests te verwerpen of te accepteren. De Student’s t-test wordt bijvoorbeeld gebruikt om hypothesen te testen voor één steekproef, voor onafhankelijke steekproeven of voor gerelateerde steekproeven. We zullen dan zien hoe de Student’s t-toets in elk geval wordt berekend.

Soorten Student’s t-tests

Er zijn drie soorten Student’s t-toetsen :

Student’s t-test met één steekproef – wordt gebruikt om de hypothese over de waarde van het steekproefgemiddelde te testen.
Student’s t-test voor twee onafhankelijke steekproeven : hiermee kunt u de hypothese testen op het verschil tussen de gemiddelden van twee onafhankelijke steekproeven.
Student’s t-test voor twee gepaarde steekproeven (of gerelateerde steekproeven) – wordt gebruikt om de hypothese over het gemiddelde van een tweemaal geteste steekproef te onderzoeken.

Een voorbeeld van Student’s t-test

Hypothesetests voor het steekproefgemiddelde zijn tests waarbij de nulhypothese en de alternatieve hypothese van de test iets zeggen over de waarde van een populatiegemiddelde.

De formule voor de Student t-test met één monster is als volgt:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Goud:

$t$

is de hypotheseteststatistiek voor het gemiddelde, dat wordt gedefinieerd door de Student’s t-verdeling.
$\overline{x}$

is het steekproefgemiddelde.
$\mu$

is de waarde van het gemiddelde dat wordt voorgesteld in de hypothesetest.
$s$

is de standaardafwijking van het monster.
$n$

is de steekproefomvang.

Zodra de waarde van de Student’s t-test is berekend, moet het resultaat van de statistische test met de kritische waarde worden geïnterpreteerd om de nulhypothese al dan niet te verwerpen:

Als de hypothesetest voor het gemiddelde tweezijdig is, wordt de nulhypothese verworpen als de absolute waarde van de Student’s t-test groter is dan de kritische waarde t _α/2|n-1 .
Als de hypothesetest voor het gemiddelde overeenkomt met de rechterstaart, wordt de nulhypothese verworpen als de t-testwaarde van de Student groter is dan de kritische waarde t _α|n-1 .
Als de hypothesetest voor het gemiddelde overeenkomt met de linkerstaart, wordt de nulhypothese verworpen als de t-testwaarde van de Student kleiner is dan de kritische waarde -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Merk op dat de kritische testwaarden worden verkregen uit de verdelingstabel van de student.

➤ Zie: Concreet voorbeeld van hypothesetoetsing voor het gemiddelde

Student’s t-test voor onafhankelijke steekproeven

De Student’s t-test voor onafhankelijke steekproeven wordt gebruikt om de hypothese van een verband tussen de gemiddelden van twee populaties te verwerpen of te accepteren, bijvoorbeeld dat de gemiddelden van twee populaties verschillend zijn of dat het gemiddelde van populatie A groter is dan het gemiddelde van . bevolking B.

In dit geval varieert de Student’s t-test-formule echter afhankelijk van het feit of kan worden aangenomen dat de populatievarianties gelijk zijn of niet. We zullen dan de twee mogelijke gevallen zien.

Onbekende en gelijke afwijkingen

De formule voor het berekenen van de Student t-toets voor onafhankelijke steekproeven wanneer de populatievarianties onbekend zijn maar verondersteld wordt gelijk te zijn, is als volgt:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Goud:

$t$

is de hypotheseteststatistiek voor het verschil tussen gemiddelden met onbekende varianties, die een Student’s t-verdeling volgt met n ₁ + n ₂ -2 vrijheidsgraden.
$\mu_1$

is het gemiddelde van populatie 1.
$\mu_2$

is het gemiddelde van populatie 2.
$\overline{x_1}$

is het gemiddelde van monster 1.
$\overline{x_2}$

is het gemiddelde van monster 2.
$s_p$

is de gepoolde standaarddeviatie.
$n_1$

is steekproefomvang 1.
$n_2$

is steekproefomvang 2.

De gecombineerde standaardafwijking van de twee monsters wordt berekend met behulp van de volgende formule:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Onbekende en verschillende varianten

Wanneer de populatievarianties onbekend zijn en bovendien aangenomen wordt dat ze verschillend zijn, is de formule voor het berekenen van de Student’s t-toets voor onafhankelijke steekproeven als volgt:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Goud:

$t$

is de hypotheseteststatistiek voor het verschil tussen gemiddelden met onbekende varianties, die de Student’s t-verdeling volgt.
$\mu_1$

is het gemiddelde van populatie 1.
$\mu_2$

is het gemiddelde van populatie 2.
$\overline{x_1}$

is het gemiddelde van monster 1.
$\overline{x_2}$

is het gemiddelde van monster 2.
$\sigma_1$

is de standaardafwijking van populatie 1.
$\sigma_2$

is de standaardafwijking van populatie 2.
$n_1$

is steekproefomvang 1.
$n_2$

is steekproefomvang 2.

In dit geval worden de vrijheidsgraden van de Student’s t-verdeling echter berekend met behulp van de volgende formule:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Zie: Concreet voorbeeld van hypothesetoetsing voor het verschil in gemiddelden

Student’s t-test voor gepaarde of gerelateerde monsters

Deze test wordt gebruikt wanneer twee onderzochte monsters aan elkaar gerelateerd zijn, zodat het feitelijk om één monster van individuen gaat dat tweemaal is geanalyseerd (elke keer onder verschillende omstandigheden).

Je kunt bijvoorbeeld de cijfers van studenten in een wiskunde- en statistiekcursus analyseren om te zien of er een significant verschil is tussen de gemiddelden voor de twee vakken. In dit geval wordt het wiskundecijfer van elke leerling gekoppeld aan het statistiekcijfer van diezelfde leerling.

De Student’s t-testformule voor gepaarde of gerelateerde monsters is:

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

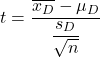
Goud:

$t$

is de hypotheseteststatistiek voor gepaarde gemiddelden, die wordt gedefinieerd door de Student’s t-verdeling.
$\overline{x_D}$

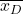
is het gemiddelde van de steekproef gevormd door het verschil in de gegevens.
$\mu_D$

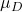
is de waarde van het gemiddelde dat wordt voorgesteld in de hypothesetest.
$s_D$

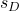
is de standaardafwijking van de steekproef, gevormd door het verschil in de gegevens.
$n$

is de steekproefomvang.

Aannames van de t-test van studenten

Om de Student’s t-toets uit te voeren, moet aan de volgende voorwaarden worden voldaan:

Continuïteit – Voorbeeldgegevens zijn continu.
Willekeurigheid : Gegevensmonsters werden willekeurig geselecteerd.
Homogeniteit : de variantie van het gegevensmonster is homogeen.
Normaliteit – De verdeling die het gegevensmonster definieert, is ongeveer normaal.

Hoe doe je een Student’s t-test?

Ten slotte worden, samengevat, de stappen beschreven die moeten worden gevolgd om een Student’s t-test uit te voeren.

Definieer de nul- en alternatieve hypothesen voor het testen van hypothesen.
Bepaal het significantieniveau (α) van de hypothesetest.
Controleer of aan de aannames van de Student’s t-test is voldaan.
Pas de overeenkomstige Student’s t-test-formule toe en bereken de teststatistiek.
Interpreteer het resultaat van de Student’s t-test door het te vergelijken met de kritische waarde van de test.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Wat is de Student’s t-toets?

Soorten Student’s t-tests

Een voorbeeld van Student’s t-test

Student’s t-test voor onafhankelijke steekproeven

Onbekende en gelijke afwijkingen

Onbekende en verschillende varianten

Student’s t-test voor gepaarde of gerelateerde monsters

Aannames van de t-test van studenten

Hoe doe je een Student’s t-test?

Über den Autor

Dr.benjamin anderson

Einen Kommentar hinzufügen