Kwaliteit van pasvorm
In dit artikel wordt uitgelegd wat goedheid van fit is in statistieken. Op dezelfde manier laat het zien hoe u de goodness of fit van een regressiemodel kunt meten en bovendien kunt u een opgeloste oefening van goodness of fit zien.
Wat is een goede pasvorm?
In de statistiek is de goodness of fit hoe goed een regressiemodel bij de gegevenssteekproef past. Met andere woorden: de ‘goodness of fit’ van een regressiemodel verwijst naar het niveau van koppeling tussen de reeks observaties en de waarden die door de regressie zijn verkregen.
Hoe beter de fit van een regressiemodel, hoe beter het de bestudeerde gegevens verklaart. We willen dus dat hoe beter het statistische model past, hoe beter.
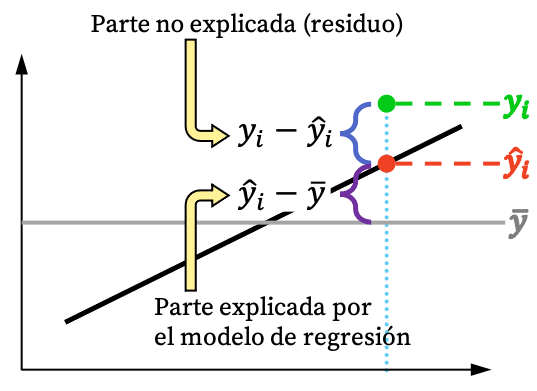
Zoals je in de afbeelding hierboven kunt zien, kan de waarde van een waarneming meestal niet volledig worden verklaard door het regressiemodel. Maar logischerwijs geldt dat hoe meer het regressiemodel uit de dataset kan verklaren, hoe beter het model zal passen. Kortom: wij zijn geïnteresseerd in een zo strak mogelijk regressiemodel.
Goede pasvorm van een regressiemodel
Om de goodness of fit van een regressiemodel te bepalen, gebruikt men doorgaans de determinatiecoëfficiënt , een statistische coëfficiënt die het percentage aangeeft dat door het regressiemodel wordt verklaard. Dus hoe hoger de determinatiecoëfficiënt van een model, hoe beter het model zal worden aangepast aan de gegevenssteekproef.
![]()
Er moet echter worden opgemerkt dat hoe meer variabelen een regressiemodel heeft, hoe hoger de determinatiecoëfficiënt zal zijn. Om deze reden wordt de aangepaste determinatiecoëfficiënt ook vaak gebruikt om de goodness of fit van een model te meten. De aangepaste determinatiecoëfficiënt is een variatie op de vorige coëfficiënt die het percentage aangeeft dat wordt verklaard door het regressiemodel, waarbij elke verklarende variabele in het model wordt bestraft.
![]()
Het verdient daarom de voorkeur om de aangepaste determinatiecoëfficiënt te gebruiken om twee modellen met een aantal verschillende variabelen te vergelijken, omdat hierbij rekening wordt gehouden met het aantal variabelen dat in het model is opgenomen.
Ten slotte moet worden opgemerkt dat de Chi-kwadraattest ook kan worden gebruikt om de goodness of fit van een regressiemodel te meten, hoewel meestal de waarden van de vorige twee coëfficiënten worden gebruikt.
Concreet voorbeeld van goede pasvorm
Ten slotte zullen we een opgeloste oefening in de kwaliteit van de aanpassing zien om de assimilatie van dit statistische concept te voltooien.
- Met dezelfde gegevensreeksen worden twee verschillende lineaire regressiemodellen uitgevoerd, waarvan u de resultaten in de volgende tabel kunt zien. Welk model kan ik het beste gebruiken?
| Regressiemodel 1 | Regressiemodel 2 | |
|---|---|---|
| Bepalingscoëfficiënt | 57% | 64% |
| Aangepaste bepalingscoëfficiënt | 49% | 43% |
| Aantal verklarende variabelen | 3 | 7 |
In dit geval gaan we ervan uit dat beide modellen voldoen aan de eerdere aannames van lineaire regressiemodellen en hoeven we daarom alleen de goede pasvorm van de modellen te analyseren.
Regressiemodel 2 heeft een hogere determinatiecoëfficiënt dan regressiemodel 1, dus het lijkt a priori een beter regressiemodel te zijn, omdat het de gegevenssteekproef beter kan verklaren.
Regressiemodel 2 heeft echter zeven onafhankelijke variabelen in het model, terwijl regressiemodel 1 er slechts drie heeft. Model 2 zal dus veel gecompliceerder en moeilijker te interpreteren zijn dan het eerste model.
Als we bovendien kijken naar de aangepaste determinatiecoëfficiënt, die rekening houdt met het aantal variabelen in het model, heeft regressiemodel 1 een hogere aangepaste determinatiecoëfficiënt dan regressiemodel 2.
Concluderend: hoewel het beter is om regressiemodel 1 te gebruiken, omdat de aangepaste determinatiecoëfficiënt hoger is dan die van regressiemodel 2. Regressiemodel 2 heeft een hogere, niet-gecorrigeerde determinatiecoëfficiënt, komt dit doordat ze veel meer variabelen in de regressie hebben opgenomen. model 1. model, dat de waarde van de genoemde coëfficiënt verhoogt, maar de interpretatie van het model moeilijker maakt en, zeker, de voorspelling van een nieuwe waarde slechter maakt.
Om modellen met verschillende aantallen variabelen te vergelijken, kunt u het beste de aangepaste determinatiecoëfficiënt gebruiken, omdat deze voor elke variabele die aan het model wordt toegevoegd, bestraft. Zoals je in dit voorbeeld hebt gezien, is regressiemodel 2 volgens de niet-aangepaste determinatiecoëfficiënt beter, maar door de aangepaste determinatiecoëfficiënt kunnen we weten dat regressiemodel 1 feitelijk beter is.