Hoe een standaarddeviatie van nul te interpreteren

In de statistieken wordt de standaardafwijking gebruikt om de verdeling van waarden in een steekproef te meten.

We kunnen de volgende formule gebruiken om de standaardafwijking van een bepaald monster te berekenen:

√ Σ(x _i – x _bar ) ² / (n-1)

Goud:

• Σ: Een symbool dat “som” betekent
• x _i : de ^i- de waarde van het monster
• x _bar : Het monster betekent
• n: De steekproefomvang

Hoe hoger de standaarddeviatiewaarde, hoe meer verspreid de waarden in een steekproef zijn.

Hoe lager de standaardafwijkingswaarde, hoe dichter de waarden bij elkaar zijn gegroepeerd.

Als de standaarddeviatie van een monster nul is, betekent dit dat alle waarden in het monster exact hetzelfde zijn.

Met andere woorden: er is geen kloof tussen de waarden.

Het volgende voorbeeld laat zien hoe u een standaarddeviatie van nul in de praktijk interpreteert.

Voorbeeld: hoe u een standaarddeviatie van nul interpreteert

Stel dat we een eenvoudig willekeurig monster van 10 hagedissen verzamelen en hun lengte meten (in inches):

Lengtes : 7, 7, 7, 7, 7, 7, 7, 7, 7, 7

De gemiddelde lengte van hagedissen in het monster is 7 inch.

Als we dit weten, kunnen we de standaardafwijking(en) van de steekproef voor deze dataset berekenen:

• s = √ Σ(x _ik – x _bar ) ² / (n-1)
• s = √ ((7 – 7) ² + (7 – 7) ² + (7 – 7) ² + … + (7 – 7) ² / (10-1)
• s = √ 0 ² + 0 ² + 0 ² + … + 0 ² / 9
• s = 0

De standaarddeviatie van de steekproef blijkt 0 te zijn.

Omdat elke hagedis exact even lang is, is de verdeling van waarden in de dataset exact nul.

Zal de standaarddeviatie in de echte wereld ooit nul zijn?

Het is heel goed mogelijk dat een dataset uit de echte wereld een standaardafwijking van nul heeft, maar dat komt zelden voor.

Het meest waarschijnlijke scenario waarin u een standaardafwijking van nul tegenkomt, is wanneer u kleine steekproeven verzamelt voor zeldzame gebeurtenissen.

Stel dat u in een bepaalde stad gedurende een periode van één week gegevens verzamelt over het aantal verkeersongevallen.

Het is heel goed mogelijk dat u de volgende gegevens verzamelt:

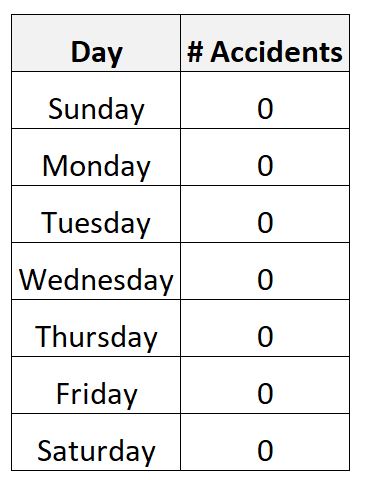
In dit scenario zou het gemiddelde aantal dagelijkse ongevallen nul zijn en zou de standaarddeviatie ook nul zijn.

Of misschien verzamelt u de volgende gegevens over het aantal maandelijkse verkopen van een duur product voor een bedrijf over een periode van zes maanden:

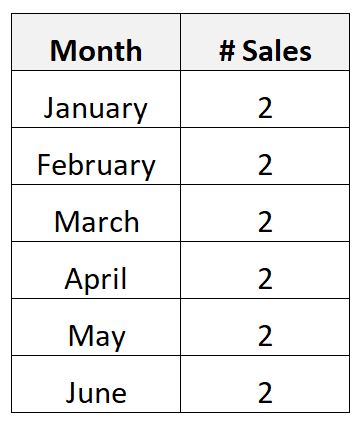
Omdat het product zo duur is, blijkt dat het bedrijf er maar precies twee per maand verkoopt.

In dit scenario is het gemiddelde aantal maandelijks verkochte producten twee en is de standaardafwijking van de maandelijks verkochte producten nul.

Wanneer u in een echte dataset een standaardafwijking van nul tegenkomt, weet dan dat dit betekent dat elke waarde in de dataset precies hetzelfde is.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over de standaarddeviatie in statistieken:

Waarom is standaarddeviatie belangrijk?
Standaardafwijking en standaardfout: wat is het verschil?
Standaarddeviatie en interkwartielbereik: wat is het verschil?