Hoe kwartielen voor gegroepeerde gegevens te berekenen

Kwartielen zijn waarden die een dataset in vier gelijke delen verdelen.

U kunt de volgende formule gebruiken om kwartielen voor gegroepeerde gegevens te berekenen:

Q _ik = L + (C/F) * (iN/4 – M)

Goud:

• L : De ondergrens van het interval dat het i- ^de kwartiel bevat
• C : De breedte van de klas
• F : De frequentie van het interval dat het i- ^de kwartiel bevat
• N : De totale frequentie
• M : De cumulatieve frequentie die leidt naar het interval dat het i- ^de kwartiel bevat

Het volgende voorbeeld laat zien hoe u deze formule in de praktijk kunt gebruiken.

Voorbeeld: Bereken kwartielen voor gegroepeerde gegevens

Stel dat we de volgende frequentieverdeling hebben:

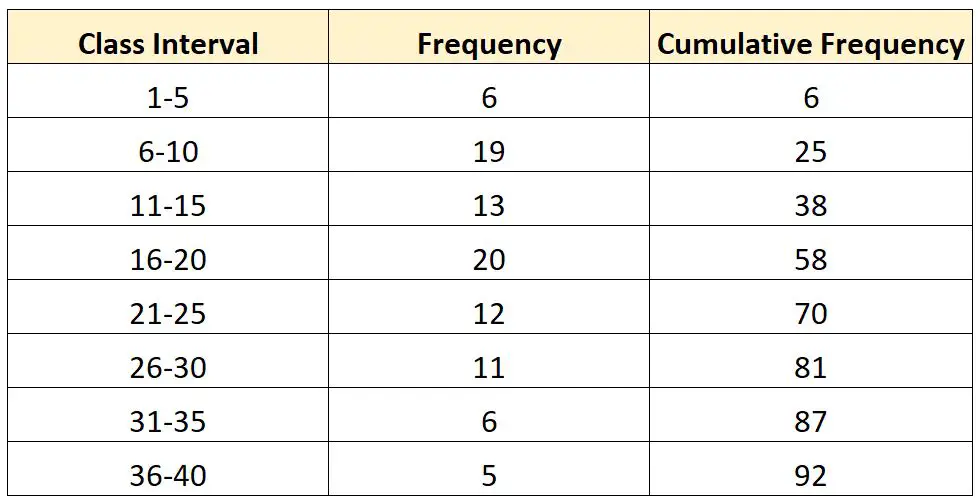
Stel nu dat we de waarde in het derde kwartiel (Q ₃ ) van deze verdeling willen berekenen.

De waarde in het derde kwartiel bevindt zich op positie (iN/4) in de verdeling.

Dus (iN/4) = (3*92/4) = 69.

Het interval dat het derde kwartiel bevat, is het interval 21-25 , aangezien 69 tussen de cumulatieve frequenties van 58 en 70 ligt.

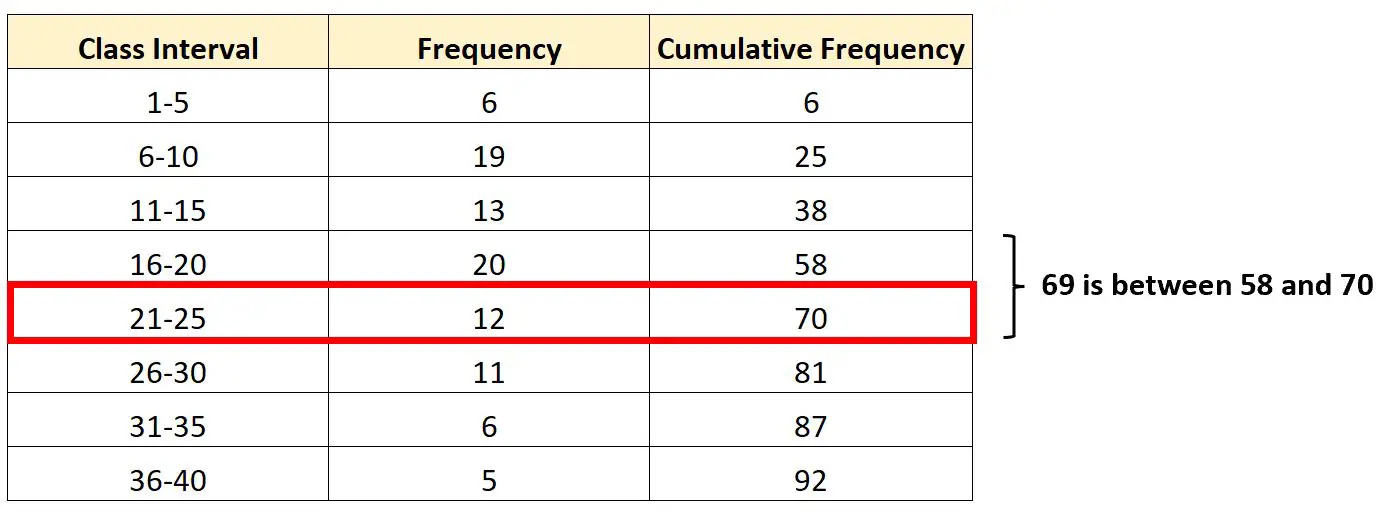
Als we dit weten, kunnen we elk van de noodzakelijke waarden vinden die we in onze formule kunnen aansluiten:

L : De ondergrens van het interval dat het i- ^de kwartiel bevat

• De ondergrens van het interval is 21 .

C : De breedte van de klas

• De breedte van de klasse wordt als volgt berekend: 25 – 21 = 4 .

F : De frequentie van het interval dat het i- ^de kwartiel bevat

• De frequentie van klasse 21-25 is 12

N : De totale frequentie

• De totale cumulatieve frequentie in de tabel is 92 .

M : De cumulatieve frequentie die leidt naar het interval dat het i- ^de kwartiel bevat

• De cumulatieve frequentie tot klasse 21-25 bedraagt 58 .

We kunnen vervolgens al deze waarden in de vorige formule pluggen om de waarde in het derde kwartiel te vinden:

• Q _ik = L + (C/F) * (iN/4 – M)
• _Q3 = 21 + (4/12) * ((3)(92)/4 – 58)
• _Q3 = 24,67

De waarde in het derde kwartiel is 24,67 .

U kunt een vergelijkbare aanpak gebruiken om de waarden van het eerste en tweede kwartiel te berekenen.

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over het werken met gegroepeerde gegevens:

Hoe u het gemiddelde en de standaardafwijking van gegroepeerde gegevens kunt vinden
Hoe de gegroepeerde gegevensmodus te vinden
Hoe u de mediaan van gegroepeerde gegevens kunt vinden
Gegroepeerde of niet-gegroepeerde frequentieverdelingen