Optellingsregel (of optellingsregel)

In dit artikel wordt uitgelegd wat de optellingsregel, ook wel de optellingsregel genoemd, is en waarvoor deze wordt gebruikt in kansrekening en statistiek. Daarnaast kun je zien wat de formule voor de optelregel is en opgeloste oefeningen die laten zien hoe je deze kunt gebruiken.

Wat is de optellingsregel (of optellingsregel)?

De optellingsregel (of optellingsregel ) stelt dat de som van de kansen op twee gebeurtenissen gelijk is aan de som van de waarschijnlijkheid dat elke gebeurtenis afzonderlijk plaatsvindt minus de waarschijnlijkheid dat beide gebeurtenissen tegelijkertijd plaatsvinden.

Daarom is de formule voor de optelregel P(A⋃B)=P(A)+P(B)−P(A⋂B).

Om dus twee waarschijnlijkheden op te tellen, kunnen we niet simpelweg elke waarschijnlijkheid optellen, omdat we ook de term moeten aftrekken die de gezamenlijke waarschijnlijkheid van de twee gebeurtenissen vertegenwoordigt. In sommige gevallen kunnen we echter alleen door de waarschijnlijkheid van elke gebeurtenis op te tellen het juiste resultaat van de som van de kansen verkrijgen. Hieronder zullen we zien welke gevallen dit zijn.

Kort gezegd wordt de optelregel gebruikt om de waarschijnlijkheid te berekenen dat de ene of de andere gebeurtenis plaatsvindt, dat wil zeggen de waarschijnlijkheid dat ten minste één van de twee mogelijke gebeurtenissen zal plaatsvinden.

Formule voor optellingsregels

De optellingsregel zegt dat om de waarschijnlijkheid te berekenen dat gebeurtenis A of gebeurtenis B plaatsvindt, we de waarschijnlijkheid dat gebeurtenis A plaatsvindt moeten optellen plus de waarschijnlijkheid dat gebeurtenis B plaatsvindt en de waarschijnlijkheid moeten aftrekken dat beide gebeurtenissen tegelijkertijd plaatsvinden. .

De formule voor de optelregel (of optelregel) is dus als volgt:

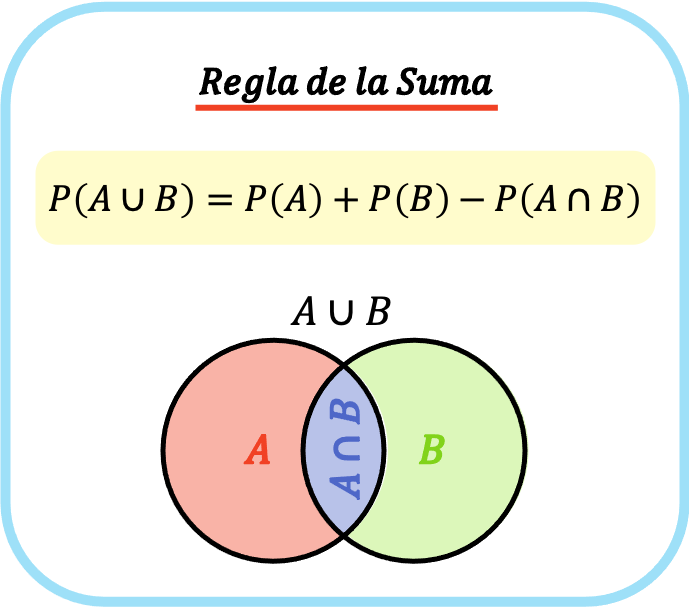
Goud:

• 

  is de waarschijnlijkheid van gebeurtenis A of gebeurtenis B.

• 

  is de kans dat gebeurtenis A zal plaatsvinden.

• 

  is de waarschijnlijkheid dat gebeurtenis B zal plaatsvinden.

• 

  is de gezamenlijke waarschijnlijkheid dat gebeurtenis A en gebeurtenis B plaatsvinden.

Om de somregel te kunnen gebruiken, moet u daarom weten hoe u de gezamenlijke waarschijnlijkheid van twee gebeurtenissen kunt berekenen. Hoe je dat doet, kun je zien via de volgende link:

Voorbeeldsomregel voor exclusieve evenementen

Laten we, om het begrip van het concept af te ronden, een voorbeeld bekijken van hoe u de optelregel toepast.

• We stoppen 10 blauwe ballen, 6 oranje ballen en 4 groene ballen in een doos. Wat is de kans dat je een blauwe of oranje bal trekt?

De oefening vraagt ons om de waarschijnlijkheid te bepalen dat de ene of de andere gebeurtenis zal plaatsvinden. Om het probleem op te lossen, moeten we daarom de optelregelformule gebruiken:

We berekenen dus eerst de waarschijnlijkheid dat elke gebeurtenis afzonderlijk plaatsvindt met behulp van de regel van Laplace :

In dit geval kunnen gebeurtenissen echter niet tegelijkertijd plaatsvinden, omdat het twee elkaar uitsluitende gebeurtenissen zijn. Dus als we een blauwe bal trekken, kunnen we niet langer een oranje bal tekenen, en omgekeerd.

Daarom is de gezamenlijke waarschijnlijkheid van beide gebeurtenissen nul en daarom is de somregelformule vereenvoudigd:

De berekening van de kans op het vangen van een blauwe bal of een oranje bal is dus als volgt:

Kortom, de kans dat je een blauwe of oranje bal uit de doos trekt is 80%.

Voorbeeld van een toevoegregel voor niet-exclusieve evenementen

Nadat we een concreet voorbeeld hebben gezien van de optellingsregel wanneer gebeurtenissen exclusief zijn, zullen we nu zien hoe deze wet wordt gebruikt wanneer gebeurtenissen niet-exclusief zijn.

• Als we twee keer een munt opgooien, wat is dan de kans dat we kop krijgen bij minstens één worp?

In dit geval sluiten de gebeurtenissen elkaar niet uit, omdat we bij de eerste worp ‘kop’ kunnen krijgen en bij de tweede worp ‘munt’. De formule voor de optelregel is dus niet vereenvoudigd en luidt als volgt:

We moeten dus eerst de waarschijnlijkheid berekenen dat we “kop” krijgen bij het opgooien van een munt door de regel van Laplace toe te passen:

Bovendien zijn de twee gebeurtenissen onafhankelijk, dus we kunnen de gezamenlijke waarschijnlijkheid van de twee gebeurtenissen berekenen met behulp van de productregel :

Ten slotte, om de waarschijnlijkheid te bepalen dat kop zal vallen bij ten minste één van de twee worpen, vervangt u eenvoudigweg de waarden in de optelregelformule en voert u de berekening uit:

Concluderend kan worden gezegd dat de kans dat door twee keer een munt op te gooien minstens één keer kop oplevert, 75% is.