Centrale limietstelling

In dit artikel wordt uitgelegd wat de centrale limietstelling (CLT) is en waarvoor deze in de statistiek wordt gebruikt. Je zult ook vinden wat de formule is van de centrale limietstelling en een voorbeeld van de toepassing ervan, stap voor stap opgelost.

Wat is de centrale limietstelling?

In de statistiek stelt de centrale limietstelling , ook wel de centrale limietstelling genoemd, dat de verdeling van de steekproefgemiddelden een normale verdeling benadert naarmate de steekproefomvang toeneemt, ongeacht de waarschijnlijkheidsverdeling van de populatie.

Dat wil zeggen, de centrale limietstelling zegt dat als we een voldoende groot aantal steekproeven nemen, het gemiddelde van die steekproeven kan worden benaderd tot een normale verdeling.

Bovendien stelt de centrale limietstelling dat het steekproefgemiddelde de waarde van het populatiegemiddelde zal benaderen naarmate de steekproefomvang toeneemt. Hierdoor kunnen we de parameters van de statistische populatie benaderen. Hieronder zullen we zien hoe dit wordt gedaan.

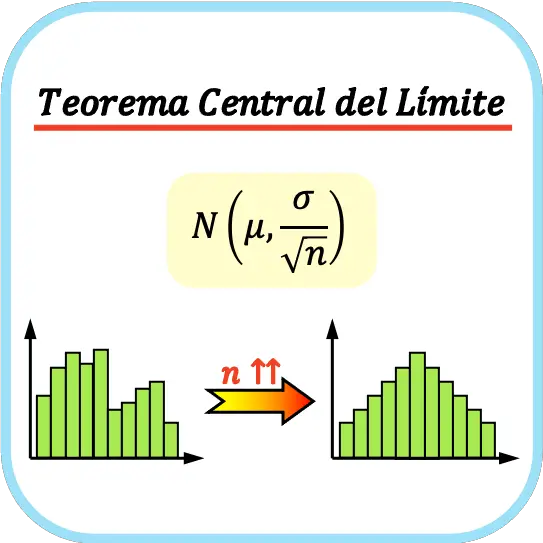
Over het algemeen wordt aangenomen dat om de centrale limietstelling toe te passen, de steekproefomvang minimaal 30 waarnemingen moet bedragen, hoewel dit afhangt van de kenmerken van de bestudeerde variabele.

De centrale limietstelling heeft veel toepassingen, aangezien de normale verdeling inferentiële statistische berekeningen mogelijk maakt, zoals het testen van hypothesen of betrouwbaarheidsintervallen. In de financiële wereld wordt de centrale limietstelling bijvoorbeeld gebruikt om het rendement en het risico van een investering te analyseren.

Voorbeeld van de centrale limietstelling

Als we eenmaal de definitie van de centrale limietstelling hebben gezien, gaan we naar een voorbeeld kijken om de betekenis ervan volledig te begrijpen.

Een voorbeeld van de centrale limietstelling is het gooien van een dobbelsteen. De dobbelstenenworp volgt een discrete, uniforme verdeling , aangezien alle uitkomsten gelijkwaardig zijn. Maar de verdeling van de som van verschillende resultaten benadert een normale verdeling.

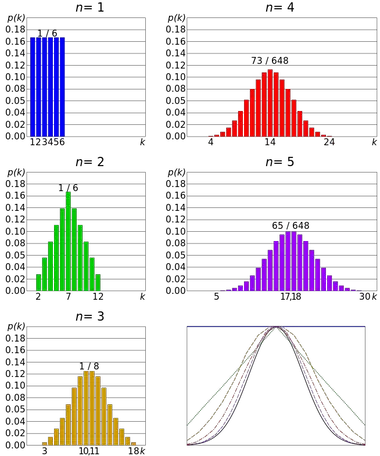
Dus hoe meer worpen er zijn, hoe waarschijnlijker het is dat de vorm van de verdeling van de middelen de neiging zal hebben om op de grafiek van de normale verdeling te lijken.

Formule van de centrale limietstelling

De centrale limietstelling stelt dat als een populatie een gemiddelde μ en standaardafwijking σ heeft en we een voldoende groot aantal steekproeven nemen (n≥30), de verzameling steekproefgemiddelden kan worden benaderd tot een normale verdeling met gemiddelde μ en standaardafwijking σ /√n.

Bovendien , _als X _{1 ,} tot een normale verdeling gedefinieerd door de volgende formule:

Opgeloste oefening van de centrale limietstelling

Zodat u het concept volledig kunt assimileren, is hier een opgeloste oefening van de centrale limietstelling.

• Een bedrijf verkoopt onderdelen die worden gebruikt om bepaalde speelgoedonderdelen te vervangen. Een munt heeft een gemiddeld gewicht van 300 gram en een standaardafwijking van 50 gram. Als een klant een partij van 100 stuks bestelt, wat is dan de kans dat het gemiddelde gewicht van de stukken in de partij groter is dan 305 g? En hoe groot is de kans dat een partij van 100 stuks meer weegt dan 31 kg?

Omdat de batchgrootte groot is (n=100), kunnen we de centrale limietstelling toepassen om het probleem op te lossen.

Met behulp van de formule van de centrale limietstelling kan de verdeling van de steekproefgemiddelden dus worden benaderd tot een normale verdeling met de volgende parameters:

Nu voeren we het typeproces uit, zodat we vervolgens de waarschijnlijkheid kunnen vinden die de oefening ons vraagt. Om dit te doen, moeten we het gemiddelde van de verdeling aftrekken en vervolgens delen door de standaardafwijking:

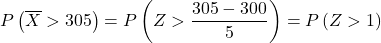normale verdelingstabel :

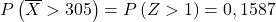
Dus we herhalen het typeproces en vinden vervolgens de tweede waarschijnlijkheid die het probleem ons vraagt:

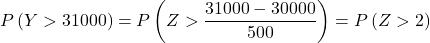
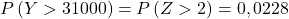➤ Zie: Wet van de grote getallen