Hoe kubieke regressie uit te voeren in python

Kubieke regressie is een type regressie dat we kunnen gebruiken om de relatie tussen een voorspellende variabele en een responsvariabele te kwantificeren wanneer de relatie tussen de variabelen niet-lineair is.

In deze tutorial wordt uitgelegd hoe u kubieke regressie uitvoert in Python.

Voorbeeld: kubieke regressie in Python

Stel dat we het volgende panda’s DataFrame hebben dat twee variabelen bevat (x en y):

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

Als we een eenvoudig spreidingsdiagram van deze gegevens maken, kunnen we zien dat de relatie tussen de twee variabelen niet-lineair is:

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

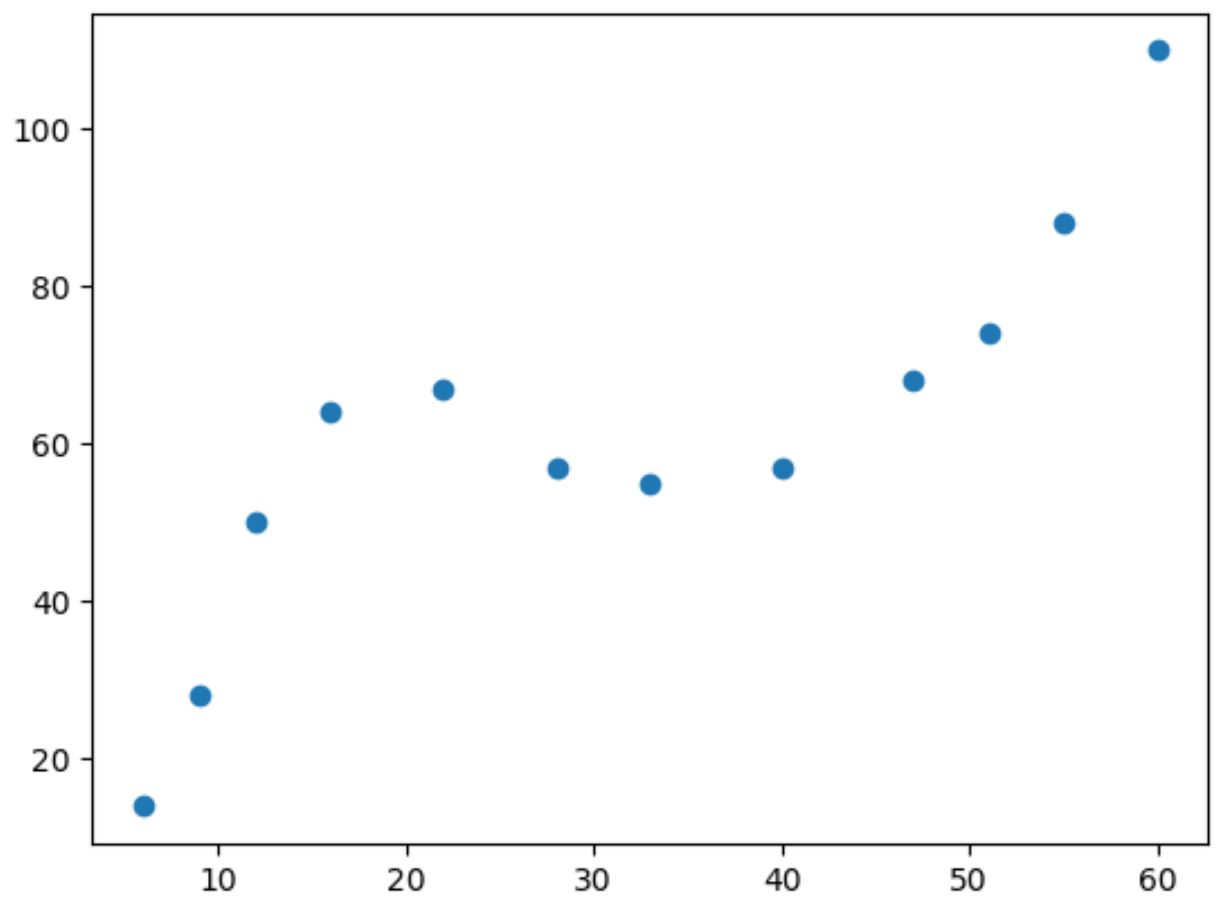
Naarmate de waarde van x toeneemt, neemt y toe tot een bepaald punt, neemt vervolgens af en neemt vervolgens weer toe.

Dit patroon met twee „curven“ in de plot is een indicatie van een kubieke relatie tussen de twee variabelen.

Dit betekent dat een kubisch regressiemodel een goede kandidaat is om de relatie tussen de twee variabelen te kwantificeren.

Om kubieke regressie uit te voeren, kunnen we een polynomiaal regressiemodel met graad 3 fitten met behulp van de numpy.polyfit() functie :

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

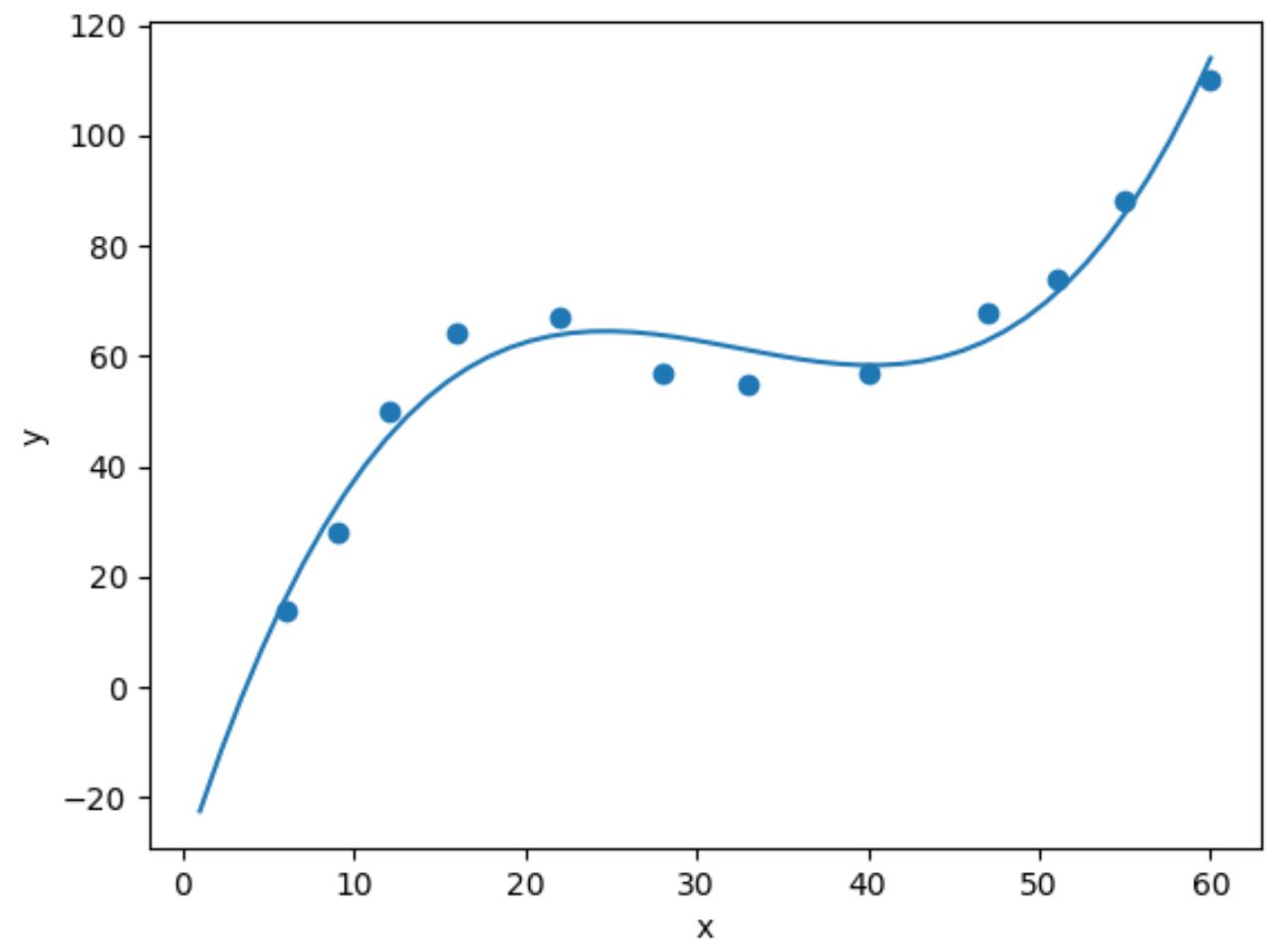
We kunnen de aangepaste kubieke regressievergelijking verkrijgen door de modelcoëfficiënten af te drukken:

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

De aangepaste kubieke regressievergelijking is:

y = 0,003302(x) ³ – 0,3214(x) ² + 9,832x – 30,01

We kunnen deze vergelijking gebruiken om de verwachte waarde van y te berekenen op basis van de waarde van x.

Als x bijvoorbeeld 30 is, dan is de verwachte waarde voor y 64,844:

y = 0,003302(30) ³ – 0,3214(30) ² + 9,832(30) – 30,01 = 64,844

We kunnen ook een korte functie schrijven om het R-kwadraat van het model te verkrijgen, wat het deel van de variantie in de responsvariabele is dat kan worden verklaard door de voorspellende variabelen.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

In dit voorbeeld is het R-kwadraat van het model 0,9632 .

Dit betekent dat 96,32% van de variatie in de responsvariabele kan worden verklaard door de voorspellende variabele.

Omdat deze waarde zo hoog is, vertelt dit ons dat het kubieke regressiemodel de relatie tussen de twee variabelen goed kwantificeert.

Gerelateerd: Wat is een goede R-kwadraatwaarde?

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in Python kunt uitvoeren:

Hoe eenvoudige lineaire regressie uit te voeren in Python
Hoe kwadratische regressie uit te voeren in Python
Hoe polynomiale regressie uit te voeren in Python