Hoe u een t-toets met ongelijke varianties uitvoert in excel

Een t-test met twee steekproeven wordt gebruikt om te bepalen of de gemiddelden van twee populaties al dan niet gelijk zijn.

Er zijn twee versies van de twee t-testvoorbeelden die u kunt gebruiken:

• t-toets met gelijke varianties
• t-toets met ongelijke varianties

We gebruiken een t-toets met ongelijke varianties wanneer de varianties van de twee steekproeven niet gelijk zijn.

De eenvoudigste manier om te bepalen of de varianties tussen de twee steekproeven gelijk zijn, is door de variantieregel te gebruiken.

Als algemene regel geldt dat als de verhouding tussen de grootste variantie en de kleinste variantie kleiner is dan 4, we kunnen aannemen dat de varianties ongeveer gelijk zijn.

Anders wordt aangenomen dat de varianties niet gelijk zijn als de verhouding gelijk is aan of groter is dan 4.

In het volgende stapsgewijze voorbeeld ziet u hoe u een t-toets met twee steekproeven met ongelijke varianties in Excel uitvoert.

Stap 1: Voer de gegevens in

Stel dat we willen bepalen of twee verschillende studiemethoden leiden tot verschillende gemiddelde examenscores onder studenten aan een bepaalde universiteit.

We selecteren een willekeurige steekproef van 20 studenten om elke studiemethode te gebruiken en hun examenresultaten vast te leggen:

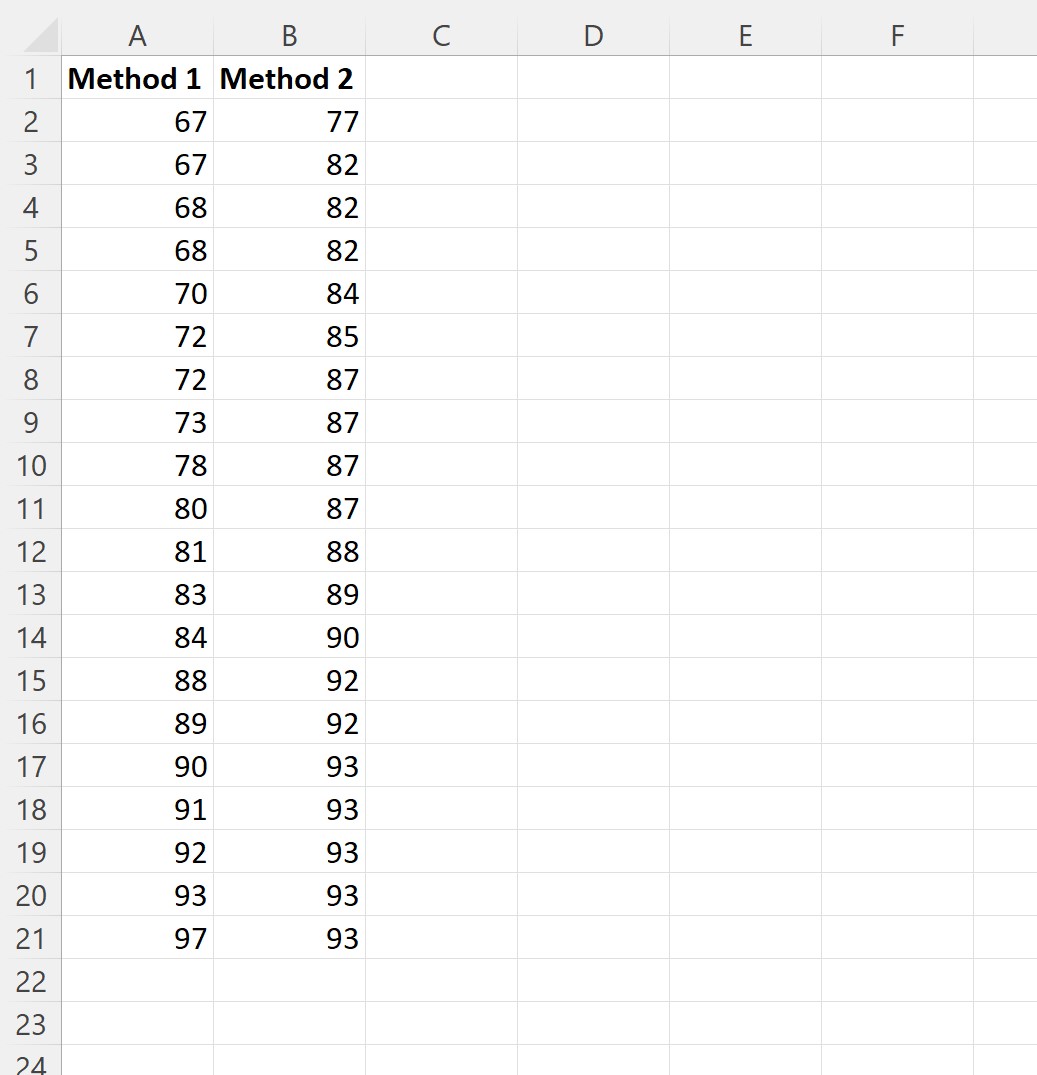
Stap 2: Bepaal gelijke of ongelijke variantie

Vervolgens kunnen we de verhouding tussen steekproefvarianties berekenen:

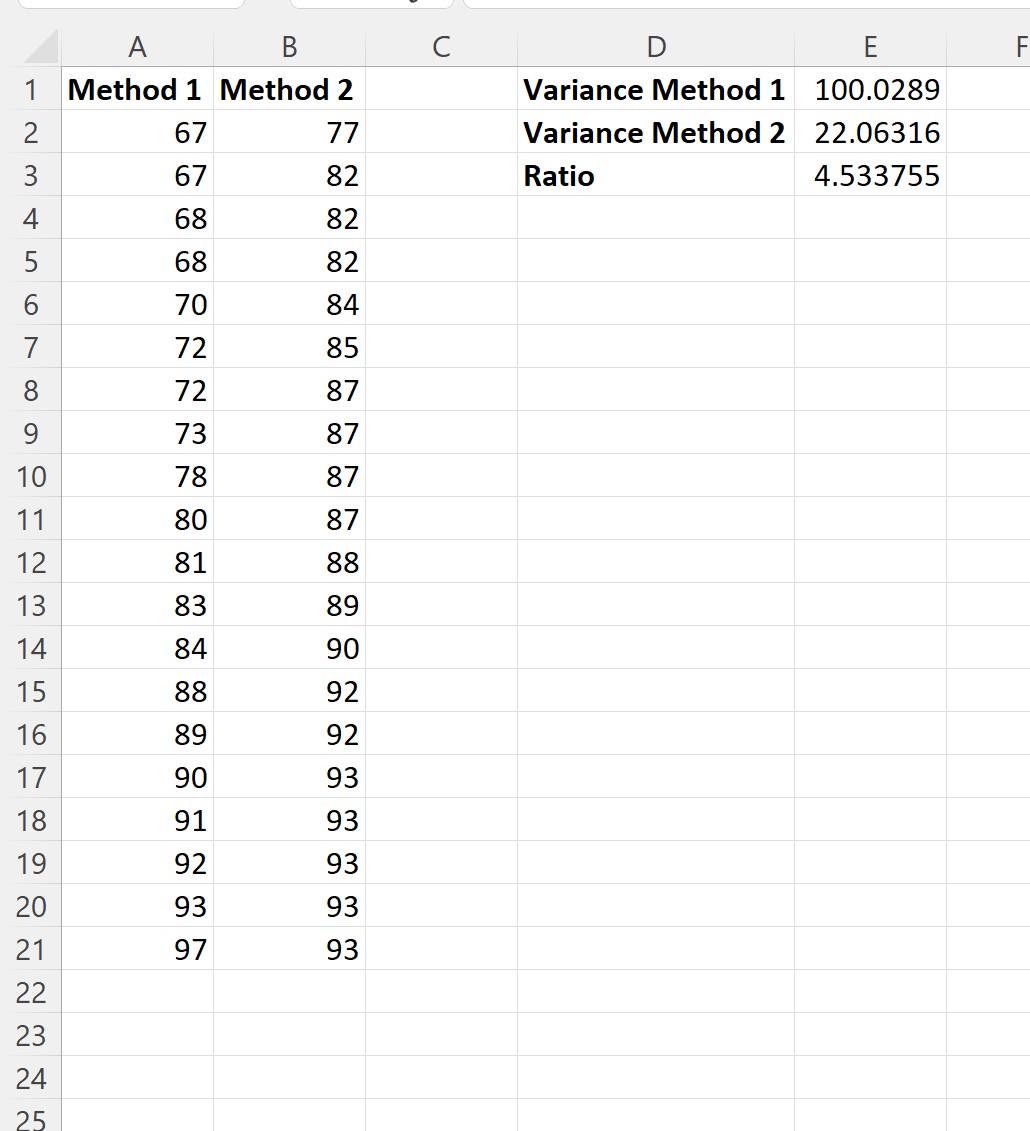
Dit zijn de formules die we in elke cel hebben getypt:

• Cel E1: =VAR.S(A2:A21)
• Cel E2: =VAR.S(B2:B21)
• Cel E3: =E1/E2

We kunnen zien dat de verhouding tussen de grootste steekproefvariantie en de kleinste steekproefvariantie 4,533755 is.

Omdat deze waarde groter is dan of gelijk is aan 4, nemen we aan dat de varianties tussen de twee steekproeven niet gelijk zijn.

Stap 3: Voer een t-test met twee steekproeven uit met ongelijke variantie

Vervolgens kunnen we een t-test met twee steekproeven met ongelijke varianties uitvoeren om te bepalen of de gemiddelde examenscore tussen de twee steekproeven gelijk is.

Om dit te doen, klikt u op het tabblad Gegevens in het bovenste lint en klikt u vervolgens op de knop Gegevensanalyse in de groep Analyseren :

Als u deze knop niet ziet, moet u eerst de gratis Data Analysis Toolpak in Excel installeren .

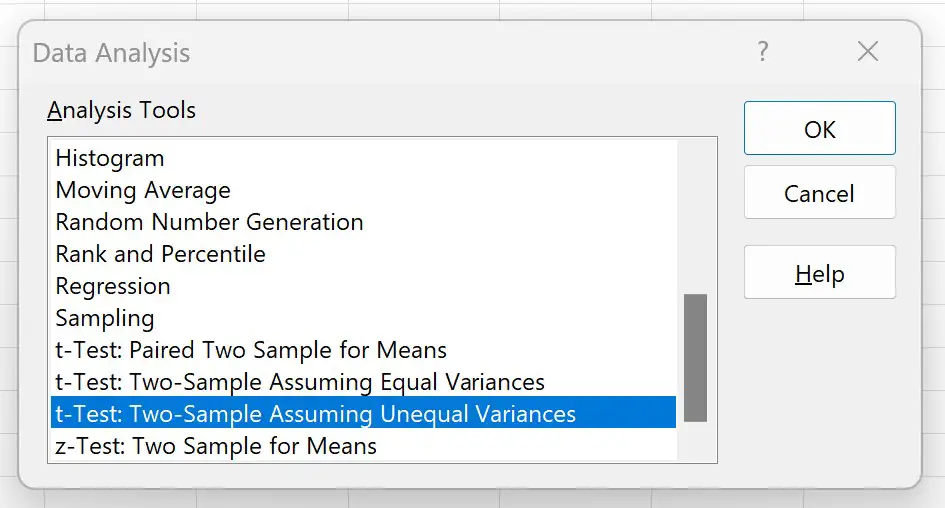
In het nieuwe venster dat verschijnt, klikt u op T-test: twee steekproeven waarbij ongelijke varianties worden aangenomen en klikt u vervolgens op OK :

Vul in het nieuwe venster dat verschijnt de volgende gegevens in en klik vervolgens op OK :

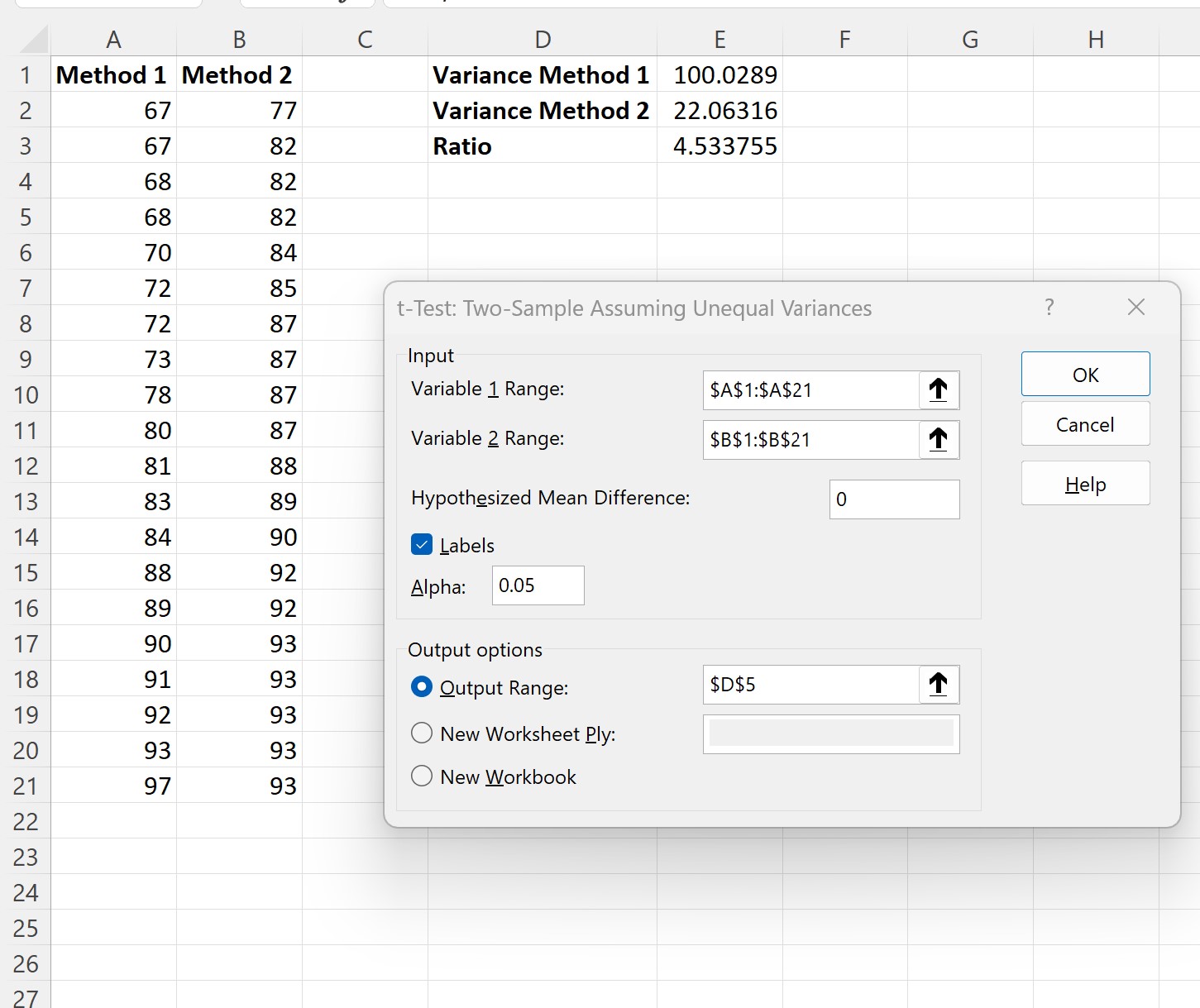
Zodra u op OK klikt, verschijnen de resultaten van de twee t-testvoorbeelden:

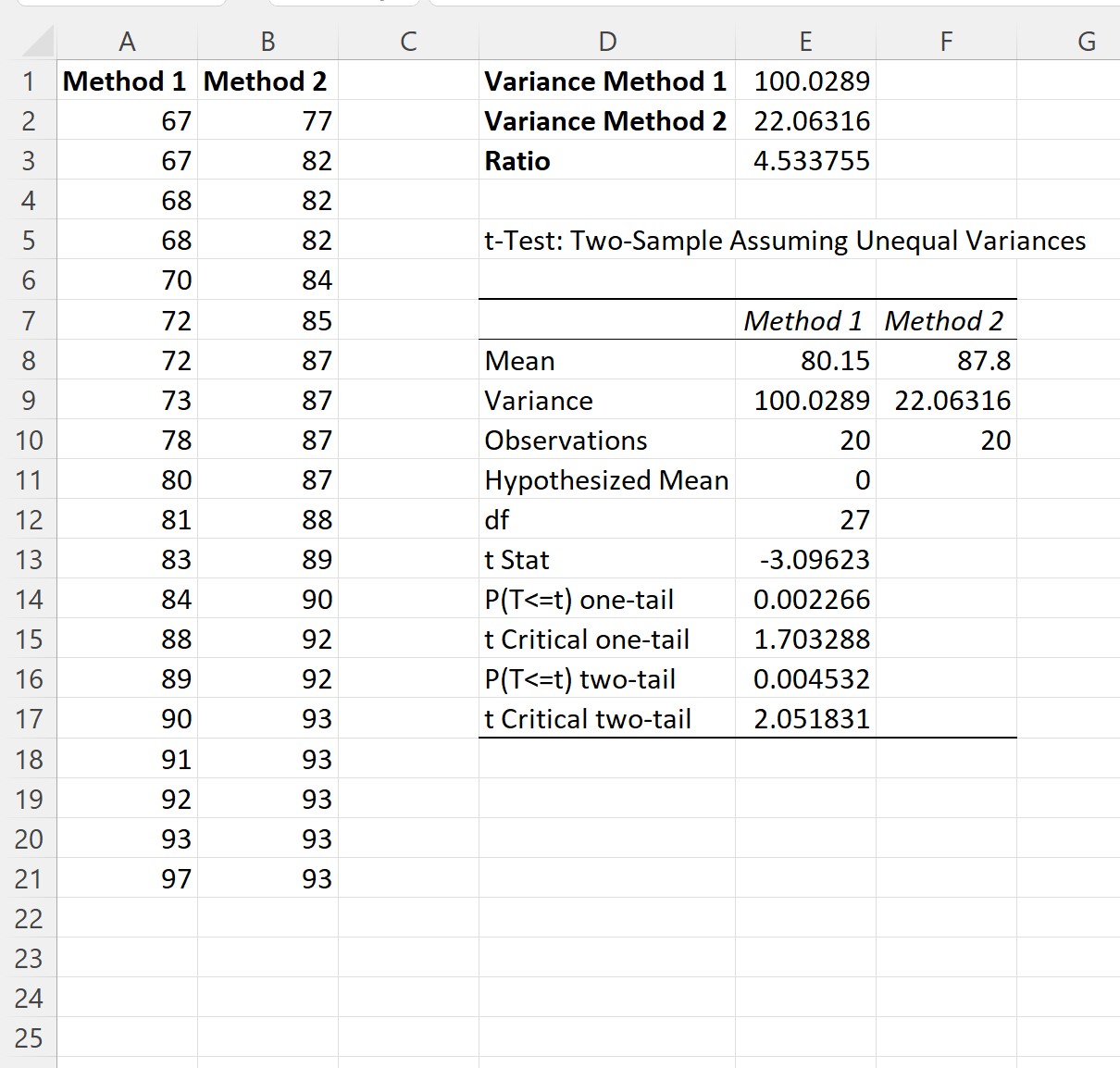
Stap 4: Interpreteer de resultaten

Uit het resultaat kunnen we zien:

• De gemiddelde examenscore voor Methode 1 was 80,15 .
• De gemiddelde examenscore voor Methode 2 was 87,8 .
• De t-teststatistiek was -3,09623 .
• De overeenkomstige tweezijdige p-waarde was 0,004532 .

Omdat deze p-waarde kleiner is dan 0,05 kunnen we concluderen dat er een statistisch significant verschil bestaat in de gemiddelde examenscores tussen de twee onderzoeksmethoden.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in Excel kunt uitvoeren:

Hoe u een t-test met één monster uitvoert in Excel
Een t-test met gepaarde monsters uitvoeren in Excel
Eén monster- en twee voorbeeld-Z-tests uitvoeren in Excel