Hoe u een best passende regel in excel maakt

In de statistiek is een best passende lijn de lijn die het beste ‘past’ of de relatie beschrijft tussen een voorspellende variabele en eenresponsvariabele .

Het volgende stapsgewijze voorbeeld laat zien hoe u een best passende lijn in Excel kunt maken.

Stap 1: Voer de gegevens in

Laten we eerst de volgende dataset invoeren die het aantal uren training en het totaal aantal punten toont dat door acht verschillende basketbalspelers is gescoord:

Stap 2: Maak een spreidingsdiagram

Laten we vervolgens een spreidingsdiagram maken om de relatie tussen de twee variabelen te visualiseren.

Om dit te doen, markeert u de cellen in het bereik A2:B9 , klikt u vervolgens op het tabblad Invoegen op het bovenste lint en klikt u vervolgens op de optie met het label Spreiding in de groep Diagrammen :

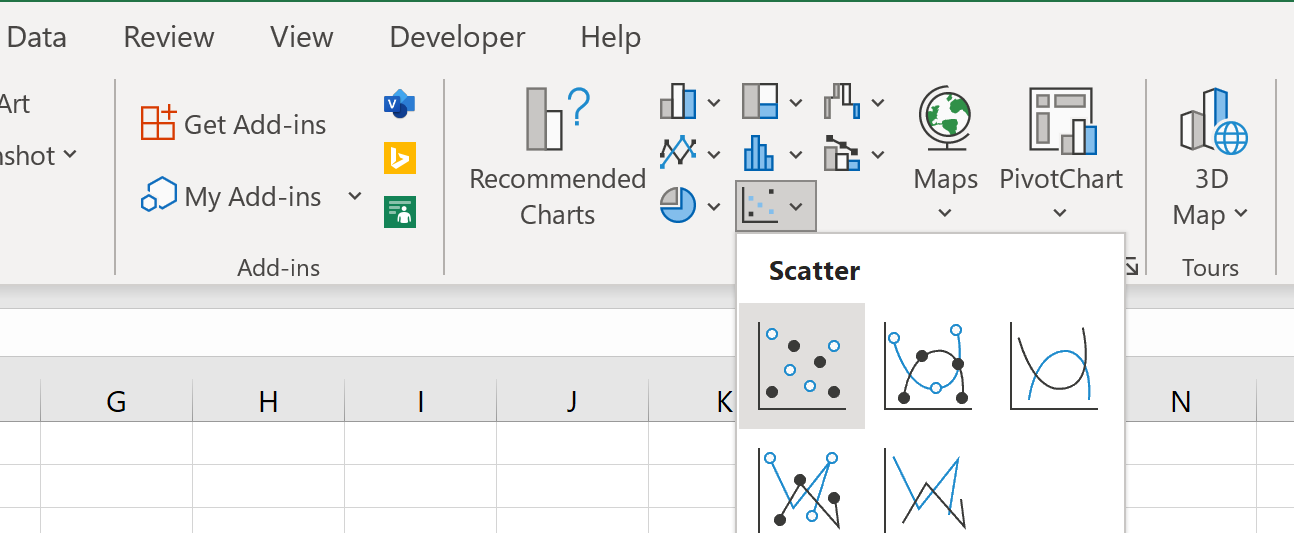
De volgende puntenwolk wordt automatisch aangemaakt:

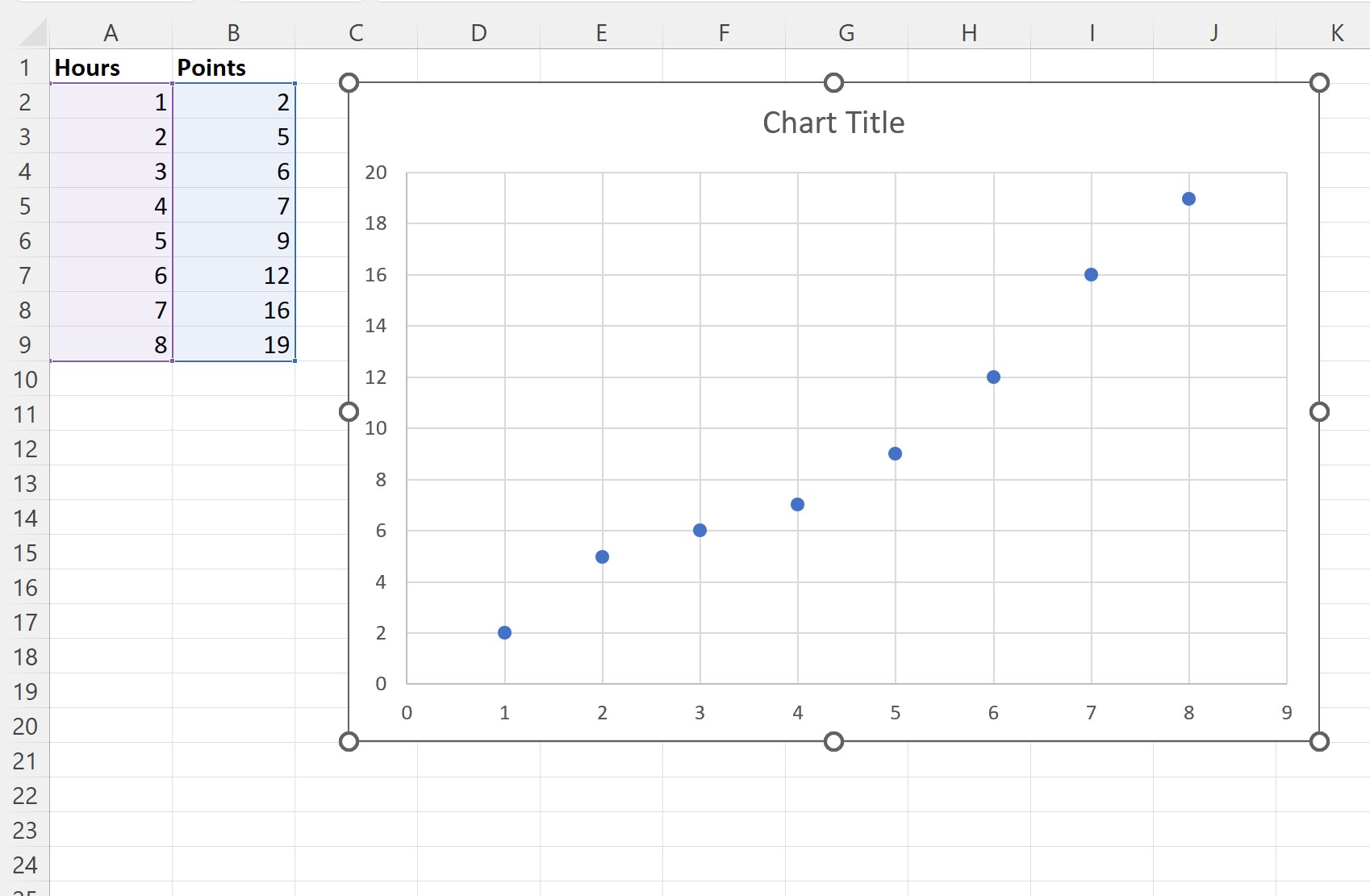
Stap 3: Voeg de best passende lijn toe

Om een best passende lijn aan het spreidingsdiagram toe te voegen, klikt u ergens in de grafiek en klikt u vervolgens op het groene plusteken (+) dat in de rechterbovenhoek van de grafiek verschijnt.

Klik vervolgens op de pijl naast Trendlijn en klik vervolgens op Meer opties :

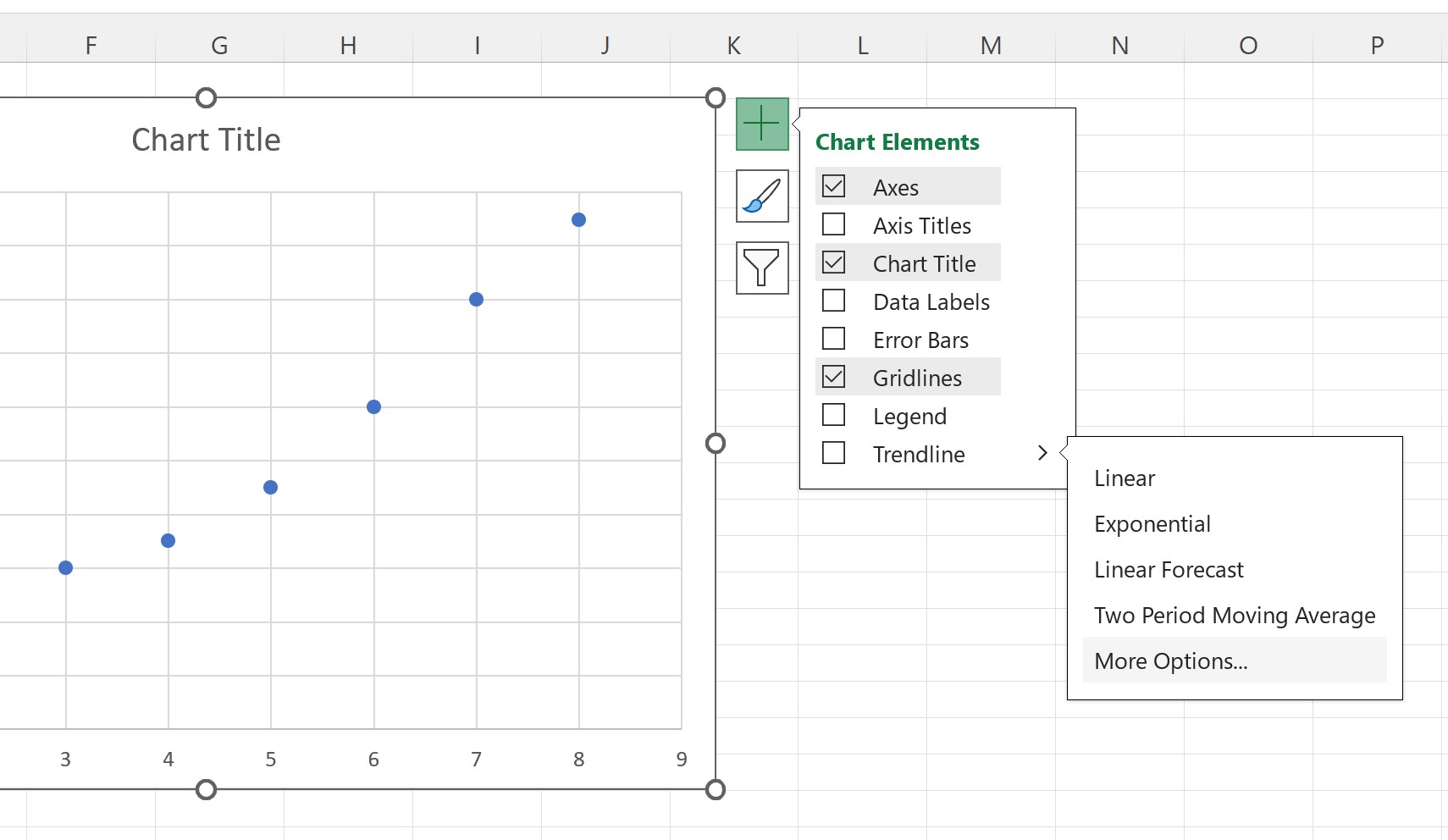
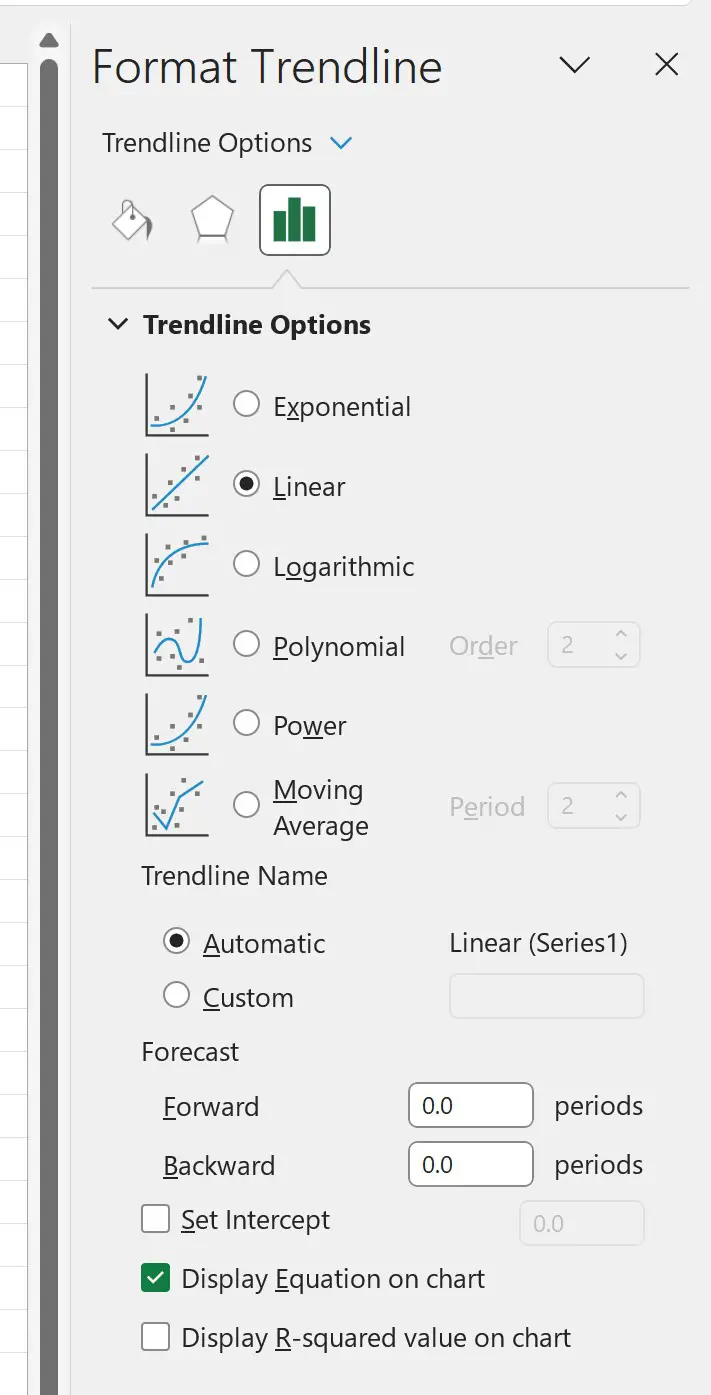
In het venster Trendlijnopmaak dat verschijnt, klikt u op de knop naast de optie Lineair als trendlijn en vinkt u vervolgens het vakje aan naast Vergelijking weergeven in diagram :

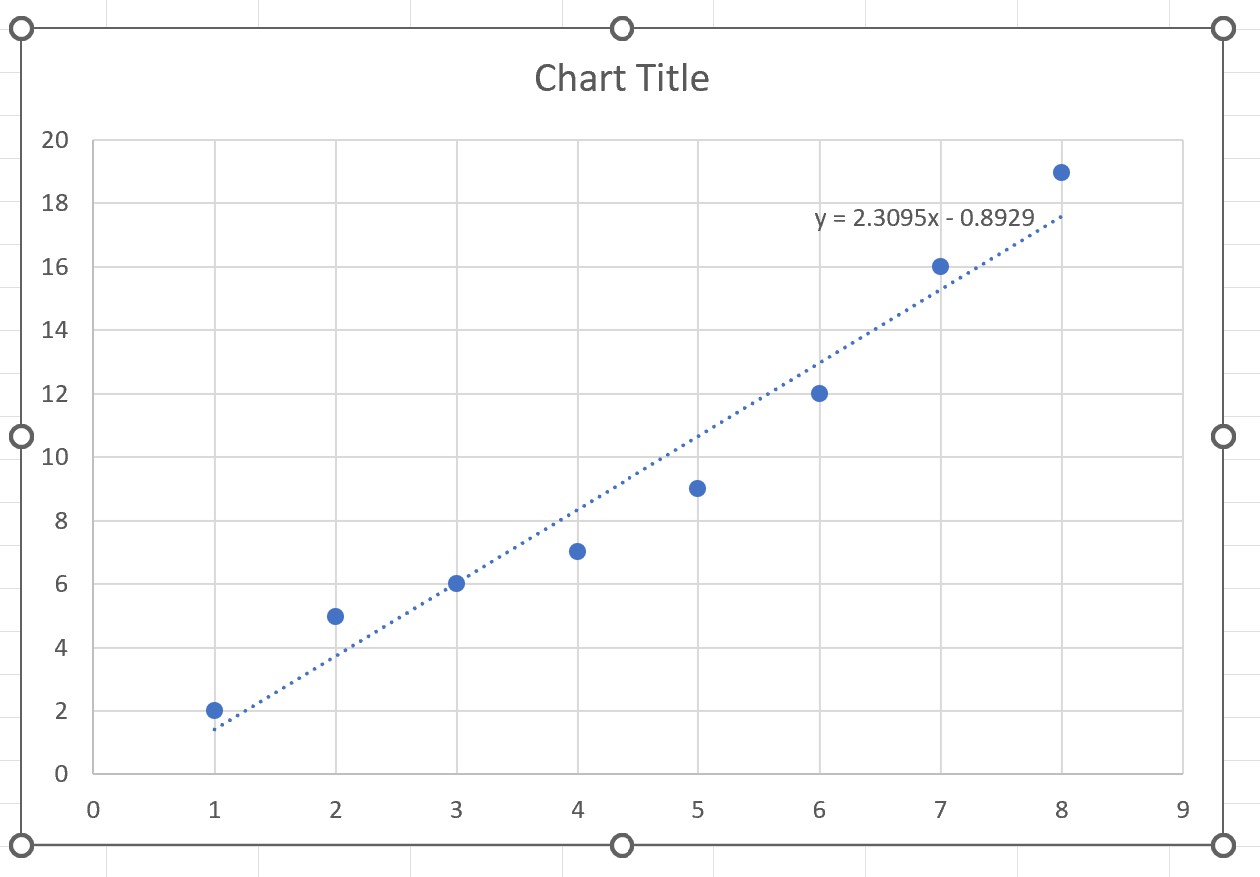
De best passende lijn en de vergelijking van de lijn verschijnen in de grafiek:

Stap 4: Interpreteer de lijn die het beste past

Uit de grafiek kunnen we zien dat de best passende lijn de volgende vergelijking heeft:

y = 2,3095x – 0,8929

Zo interpreteert u deze vergelijking:

• Voor elk extra uur dat wordt besteed aan oefenen, stijgt het gemiddelde aantal punten met 2,3095 .
• Voor een speler die nul uur oefent, moet het gemiddelde aantal gescoorde punten -0,8929 zijn.

Merk op dat het niet altijd zinvol is om de oorspronkelijke waarde in een regressievergelijking te interpreteren.

Het is bijvoorbeeld niet mogelijk dat een speler negatieve punten scoort.

In dit specifieke voorbeeld zijn we vooral geïnteresseerd in de waarde van de helling van de regressielijn, namelijk 2,3095 .

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in Excel kunt uitvoeren:

Hoe u eenvoudige lineaire regressie uitvoert in Excel
Hoe u meerdere lineaire regressies uitvoert in Excel
Hoe R-kwadraat te berekenen in Excel