Hoe p-waarden in excel te berekenen (3 voorbeelden)

In de statistiek gebruiken we hypothesetoetsen om te bepalen of een uitspraak over een populatieparameter waar is of niet.

Wanneer we een hypothesetest uitvoeren, krijgen we vaak een T-score-teststatistiek.

Zodra we deze t-score-teststatistiek hebben gevonden, kunnen we de bijbehorende p-waarde vinden.

Als deze p-waarde kleiner is dan een bepaalde waarde (bijvoorbeeld 0,10, 0,05, 0,01), dan verwerpen we de nulhypothese van de test en concluderen we dat onze resultaten statistisch significant zijn.

De volgende voorbeelden laten zien hoe u een p-waarde voor een teststatistiek in Excel in drie verschillende scenario’s kunt berekenen.

Voorbeeld 1: Bereken de P-waarde voor een tweezijdige toets

Stel dat een botanicus wil weten of de gemiddelde hoogte van een bepaalde plantensoort gelijk is aan 45 centimeter.

In een willekeurige steekproef van 12 planten ontdekt ze dat de gemiddelde hoogte van het monster 40,5 cm bedraagt en de standaardafwijking van het monster 1,37 cm.

Het voert een hypothesetest uit met behulp van de volgende nul- en alternatieve hypothesen:

H ₀ (nulhypothese): μ= 15 inch

_HA (alternatieve hypothese): μ ≠ 15 inch

De teststatistiek wordt als volgt berekend:

• t = ( X – µ) / (s/ √n )
• t = (14,33-15) / (1,37/√ 12 )
• t = -1,694

De vrijheidsgraden die bij deze teststatistiek horen, zijn n-1 = 12-1 = 11 .

Om de p-waarde voor deze teststatistiek te vinden, gebruiken we de volgende formule in Excel:

 =T.DIST.2T(ABS(-1.694), 11)

De volgende schermafbeelding laat zien hoe u deze formule in de praktijk kunt gebruiken.

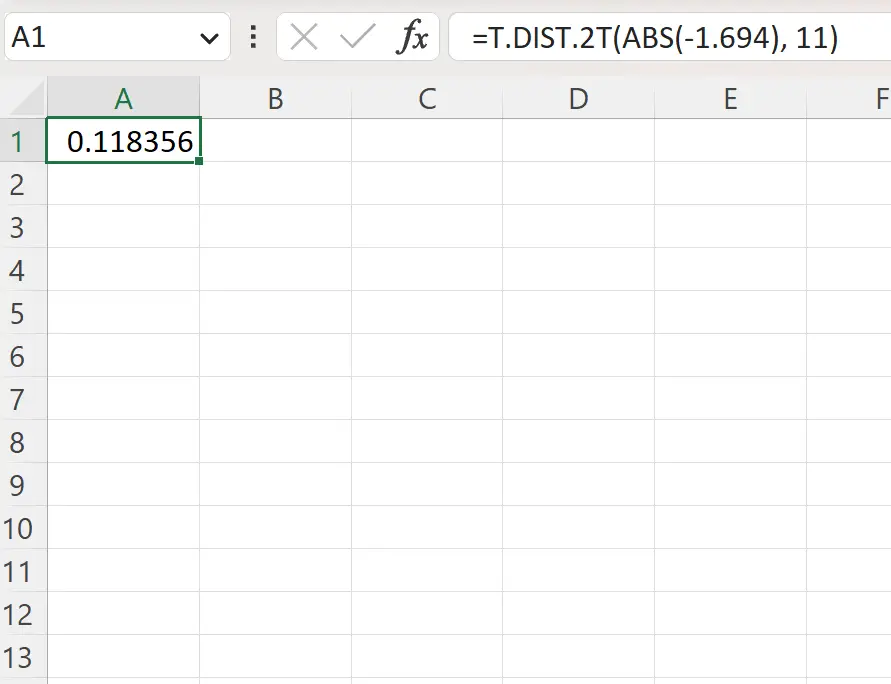
De tweezijdige p-waarde is 0,1184 .

Sinds deze waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. We hebben niet genoeg bewijs om te zeggen dat de gemiddelde planthoogte anders is dan 15 inch.

Voorbeeld 2: Bereken de P-waarde voor de test aan de linkerkant

Stel dat we aannemen dat het gemiddelde gewicht van een bepaald gadget dat in een fabriek wordt geproduceerd 20 gram bedraagt. Een inspecteur schat het werkelijke gemiddelde gewicht echter op minder dan 20 gram.

Om dit te testen, weegt het een eenvoudige willekeurige steekproef van 20 widgets en krijgt het de volgende informatie:

• n = 20 widgets
• x = 19,8 gram
• s = 3,1 gram

Vervolgens voert het een hypothesetest uit met behulp van de volgende nul- en alternatieve hypothesen:

H ₀ (nulhypothese): μ ≥ 20 gram

_HA (alternatieve hypothese): μ < 20 gram

De teststatistiek wordt als volgt berekend:

• t = ( X – µ) / (s/ √n )
• t = (19,8-20) / (3,1/√ 20 )
• t = -.2885

De vrijheidsgraden die bij deze teststatistiek horen, zijn n-1 = 20-1 = 19 .

Om de p-waarde voor deze teststatistiek te vinden, gebruiken we de volgende formule in Excel:

 =T.DIST(-.2885, 19, TRUE)

De volgende schermafbeelding laat zien hoe u deze formule in de praktijk kunt gebruiken.

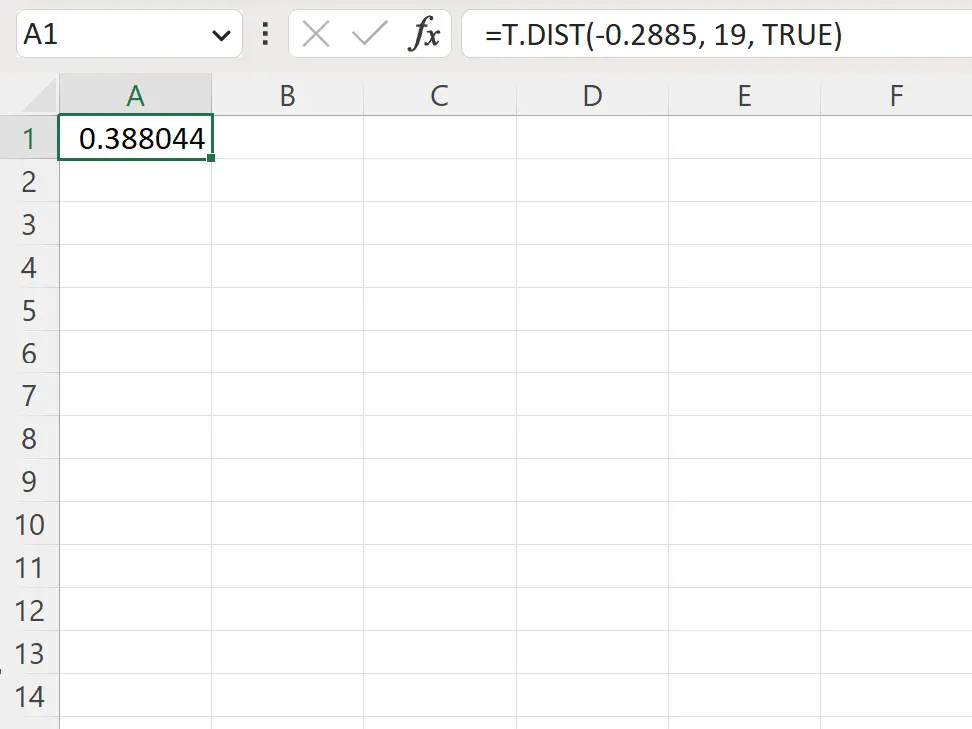
De p-waarde aan de linkerkant is 0,388044 .

Sinds deze waarde niet kleiner is dan 0,05, slaagt de inspecteur er niet in de nulhypothese te verwerpen. Er is onvoldoende bewijs om te zeggen dat het werkelijke gemiddelde gewicht van de in deze fabriek geproduceerde widgets minder dan 20 gram bedraagt.

Opmerking : we hebben het TRUE- argument gebruikt om te specificeren dat de cumulatieve verdelingsfunctie moet worden gebruikt bij het berekenen van de p-waarde.

Voorbeeld 3: Bereken de P-waarde voor de rechtszijdige toets

Laten we aannemen dat de gemiddelde hoogte van een bepaalde plantensoort 25 cm is. Eén botanicus zegt echter dat de werkelijke gemiddelde hoogte meer dan 25 centimeter bedraagt.

Om deze bewering te testen, meet ze de hoogte van een eenvoudig willekeurig monster van 15 planten en krijgt ze de volgende informatie:

• n = 15 planten
• x = 11,4 inch
• s = 2,5 inch

Vervolgens voert het een hypothesetest uit met behulp van de volgende nul- en alternatieve hypothesen:

H ₀ (nulhypothese): μ ≤ 10 inch

_HA (alternatieve hypothese): μ > 10 inch

De teststatistiek wordt als volgt berekend:

• t = ( X – µ) / (s/ √n )
• t = (11,4-10) / (2,5/√ 15 )
• t = 2,1689

De vrijheidsgraden die bij deze teststatistiek horen, zijn n-1 = 15-1 = 14 .

Om de p-waarde voor deze teststatistiek te vinden, gebruiken we de volgende formule in Excel:

 =T.DIST.RT(2.1689, 14)

De volgende schermafbeelding laat zien hoe u deze formule in de praktijk kunt gebruiken.

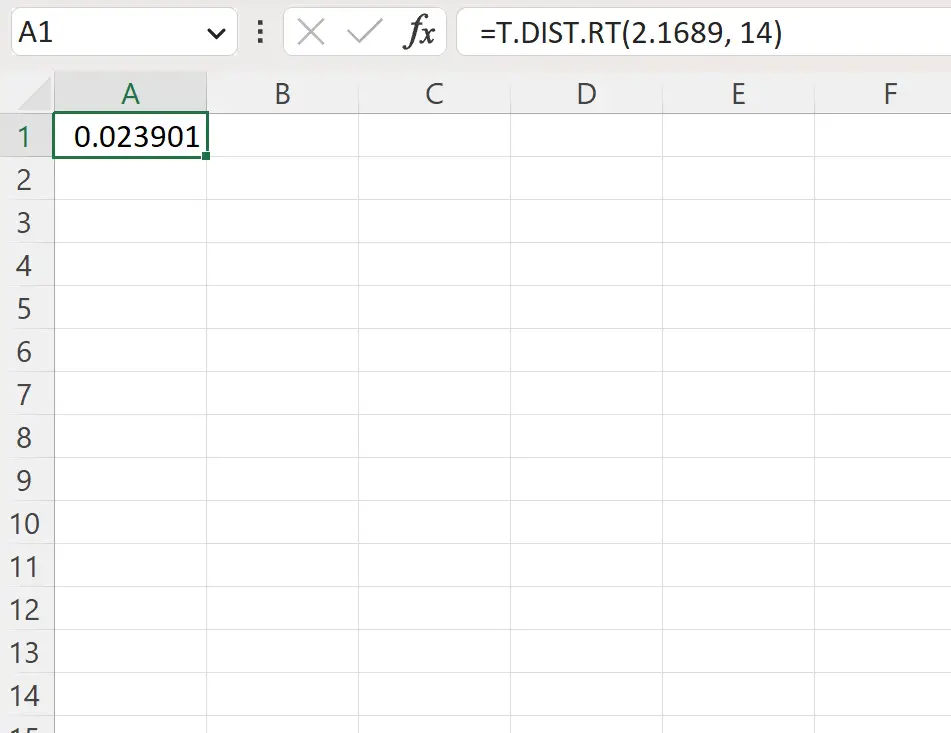
De p-waarde aan de rechterkant is 0,023901 .

Omdat deze waarde kleiner is dan 0,05, kan de botanicus de nulhypothese verwerpen. Ze heeft genoeg bewijs om te zeggen dat de werkelijke gemiddelde hoogte van deze plantensoort meer dan 25 centimeter bedraagt.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in Excel kunt uitvoeren:

Hoe u een P-waarde kunt vinden uit een Z-score in Excel
Hoe u de P-waarde van een F-statistiek in Excel kunt vinden
Hoe u de P-waarde van een chikwadraatstatistiek in Excel kunt vinden