Effectgrootte: wat het is en waarom het ertoe doet
“De statistische significantie is het minst interessante aan de resultaten. Je moet de resultaten beschrijven in termen van omvang; niet alleen heeft een behandeling invloed op mensen, maar ook in welke mate deze op hen van invloed is. -Gene V. Glas
In de statistiek gebruiken we vaak p-waarden om te bepalen of er een statistisch significant verschil is tussen twee groepen.
Laten we bijvoorbeeld zeggen dat we willen weten of twee verschillende studietechnieken tot verschillende testscores leiden. We hebben dus een groep van 20 studenten die één studietechniek gebruiken om zich voor te bereiden op een toets, terwijl een andere groep van 20 studenten een andere studietechniek gebruikt. Vervolgens geven we iedere leerling dezelfde toets.
Na het uitvoeren van een t-test met twee steekproeven om een verschil in gemiddelden te bepalen, ontdekken we dat de p-waarde voor de test 0,001 is. Als we een significantieniveau van 0,05 gebruiken, betekent dit dat er een statistisch significant verschil bestaat tussen de gemiddelde resultaten van de twee groepen. De studietechniek heeft dus invloed op de toetsresultaten.
Hoewel de p-waarde ons vertelt dat het bestuderen van techniek een impact heeft op de testscores, vertelt deze ons niet de omvang van die impact. Om dit te begrijpen moeten we de effectgrootte kennen.
Wat is effectgrootte?
Een effectgrootte is een manier om het verschil tussen twee groepen te kwantificeren.
Hoewel een p-waarde ons kan vertellen of er al dan niet een statistisch significant verschil is tussen twee groepen, kan een effectgrootte ons vertellen hoe groot dat verschil werkelijk is. In de praktijk zijn effectgroottes veel interessanter en nuttiger om te weten dan p-waarden.
Er zijn drie manieren om de effectgrootte te meten, afhankelijk van het type analyse dat u uitvoert:
1. Gestandaardiseerd gemiddeld verschil
Als je het gemiddelde verschil tussen twee groepen wilt bestuderen, is de juiste manier om de effectgrootte te berekenen het gebruik van een gestandaardiseerd gemiddeld verschil . De meest populaire formule om te gebruiken staat bekend als Cohen’s d , die als volgt wordt berekend:
Cohen ’s D = ( x1 – x2 )/ s
waarbij x 1 en x 2 de steekproefgemiddelden zijn van respectievelijk groep 1 en groep 2, en s de standaardafwijking is van de populatie waaruit de twee groepen zijn getrokken.
Met behulp van deze formule is de effectgrootte eenvoudig te interpreteren:
- Een d van 1 geeft aan dat de gemiddelden van de twee groepen één standaarddeviatie verschillen.
- Een d van 2 betekent dat de groepsgemiddelden twee standaarddeviaties verschillen.
- Een d van 2,5 geeft aan dat de twee gemiddelden 2,5 standaarddeviaties verschillen, enzovoort.
Een andere manier om de effectgrootte te interpreteren is: een effectgrootte van 0,3 betekent dat de score van de gemiddelde persoon in Groep 2 0,3 standaardafwijkingen boven het persoonsgemiddelde van groep 1 ligt en dus hoger is dan de scores van 62% van die van groep 1 . .
De volgende tabel toont verschillende effectgroottes en de bijbehorende percentielen:
| Effectgrootte | Percentage van groep 2 dat onder het gemiddelde van mensen in groep 1 zou liggen |
|---|---|
| 0,0 | 50% |
| 0,2 | 58% |
| 0,4 | 66% |
| 0,6 | 73% |
| 0,8 | 79% |
| 1,0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99,9% |
Hoe groter de effectgrootte, hoe groter het verschil tussen het gemiddelde individu in elke groep.
Over het algemeen wordt een d van 0,2 of minder als een kleine effectgrootte beschouwd, een d van ongeveer 0,5 als een gemiddelde effectgrootte en een d van 0,8 of groter als een grote effectgrootte.
Dus als de gemiddelden van twee groepen niet minstens 0,2 standaarddeviaties verschillen, is het verschil onbeduidend, zelfs als de p-waarde statistisch significant is.
2. Correlatiecoëfficiënt
Wanneer u de kwantitatieve relatie tussen twee variabelen wilt bestuderen, is de meest gebruikelijke manier om de effectgrootte te berekenen het gebruik van dePearson-correlatiecoëfficiënt . Het is een maatstaf voor de lineaire associatie tussen twee variabelen X en Y. Het heeft een waarde tussen -1 en 1 waarbij:
- -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
- 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
- 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen
De formule voor het berekenen van de Pearson-correlatiecoëfficiënt is behoorlijk complex, maar kan hier worden gevonden voor geïnteresseerden.
Hoe verder de correlatiecoëfficiënt van nul verwijderd is, hoe sterker het lineaire verband tussen twee variabelen. Dit is ook te zien door een eenvoudig spreidingsdiagram te maken van de waarden van de variabelen X en Y.
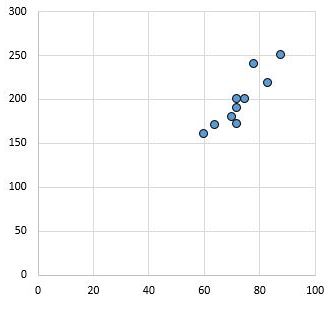
Het volgende spreidingsdiagram toont bijvoorbeeld de waarden van twee variabelen met een correlatiecoëfficiënt van r = 0,94.
Deze waarde is verre van nul, wat aangeeft dat er een sterk positief verband bestaat tussen de twee variabelen.
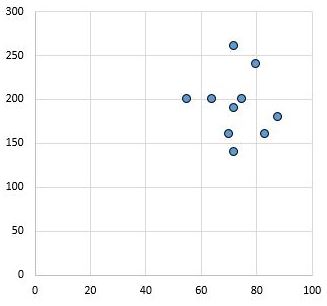
Omgekeerd toont het volgende spreidingsdiagram de waarden van twee variabelen met een correlatiecoëfficiënt van r = 0,03. Deze waarde ligt dicht bij nul, wat aangeeft dat er vrijwel geen verband bestaat tussen de twee variabelen.
Over het algemeen wordt de effectgrootte als klein beschouwd als de waarde van de Pearson-correlatiecoëfficiënt r ongeveer 0,1 is, gemiddeld als r ongeveer 0,3 is, en groot als r gelijk is aan of groter is dan 0,5.
3. Kansenratio
Als je de kans op succes in een behandelgroep wilt onderzoeken versus de kans op succes in een controlegroep, is de meest gebruikelijke manier om de effectgrootte te berekenen het gebruik van de odds ratio .
Stel dat we bijvoorbeeld de volgende tabel hebben:
| Effectgrootte | #Succes | #Schaken |
|---|---|---|
| Behandelingsgroep | HEEFT | B |
| Controlegroep | VS | D |
De odds ratio zou als volgt worden berekend:
Odds-ratio = (AD) / (BC)
Hoe verder de odds ratio van 1 af ligt, hoe groter de kans dat de behandeling een reëel effect zal hebben.
De voordelen van het gebruik van effectgroottes boven P-waarden
Effectgroottes hebben verschillende voordelen ten opzichte van p-waarden:
1. Een effectgrootte helpt ons een beter beeld te krijgen van hoe groot het verschil is tussen twee groepen of hoe sterk de associatie is tussen twee groepen. Een p-waarde kan ons alleen vertellen of er al dan niet een significant verschil of een significant verband bestaat .
2. In tegenstelling tot p-waarden kunnen effectgroottes worden gebruikt om de resultaten van verschillende onderzoeken die in verschillende settings zijn uitgevoerd kwantitatief te vergelijken. Om deze reden worden effectgroottes vaak gebruikt in meta-analyses.
3. P-waarden kunnen worden beïnvloed door grote steekproeven. Hoe groter de steekproefomvang, hoe groter de statistische kracht van een hypothesetest, waardoor zelfs kleine effecten kunnen worden gedetecteerd. Dit kan leiden tot lage p-waarden, ondanks kleine effectgroottes die mogelijk geen praktische betekenis hebben.
Een eenvoudig voorbeeld kan dit duidelijk illustreren: stel dat we willen weten of twee studietechnieken tot verschillende toetsscores leiden. We hebben een groep van 20 studenten die één studietechniek gebruiken, terwijl een andere groep van 20 studenten een andere studietechniek gebruikt. Vervolgens geven we iedere leerling dezelfde toets.
De gemiddelde score van groep 1 is 90,65 en de gemiddelde score van groep 2 is 90,75 . De standaardafwijking voor monster 1 is 2,77 en de standaardafwijking voor monster 2 is 2,78 .
Wanneer we een onafhankelijke t-test met twee steekproeven uitvoeren, blijkt dat de teststatistiek -0,113 is en de overeenkomstige p-waarde 0,91 . Het verschil tussen de gemiddelde testscores is niet statistisch significant.
Bedenk echter of de steekproefomvang van de twee steekproeven beide 200 was, maar dat de gemiddelden en standaarddeviaties exact hetzelfde bleven.
In dit geval zou een onafhankelijke t-test met twee steekproeven onthullen dat de teststatistiek -1,97 is en de overeenkomstige p-waarde net onder 0,05 ligt. Het verschil tussen de gemiddelde testscores is statistisch significant.
De onderliggende reden waarom grote steekproefgroottes tot statistisch significante conclusies kunnen leiden, is te wijten aan de formule die wordt gebruikt om t- teststatistieken te berekenen:
teststatistiek t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
Merk op dat wanneer n 1 en n 2 klein zijn, de gehele noemer van de t -teststatistiek klein is. En als je deelt door een klein getal, krijg je een groot getal. Dit betekent dat de t- teststatistiek groot zal zijn en de overeenkomstige p-waarde klein, wat tot statistisch significante resultaten zal leiden.
Wat wordt als een goede effectgrootte beschouwd?
Een vraag die studenten vaak stellen is: wat wordt als een goede effectgrootte beschouwd?
Het korte antwoord: een effectgrootte kan niet ‘goed’ of ‘slecht’ zijn, omdat deze eenvoudigweg de grootte van het verschil tussen twee groepen of de sterkte van de associatie tussen twee groepen meet.
We kunnen echter de volgende vuistregels gebruiken om te kwantificeren of de omvang van een effect klein, middelgroot of groot is:
Cohens D:
- Een d van 0,2 of minder wordt als een kleine effectgrootte beschouwd.
- Een d van 0,5 wordt als een gemiddelde effectgrootte beschouwd.
- Een d van 0,8 of groter wordt als een grote effectgrootte beschouwd.
Pearson-correlatiecoëfficiënt
- Een absolute waarde van r rond de 0,1 wordt als een kleine effectgrootte beschouwd.
- Een absolute waarde van r rond de 0,3 wordt als een gemiddelde effectgrootte beschouwd.
- Een absolute waarde van r groter dan 0,5 wordt als een grote effectgrootte beschouwd.
De definitie van een ‘sterke’ correlatie kan echter van veld tot veld verschillen. Raadpleeg dit artikel om beter te begrijpen wat wordt beschouwd als een sterke correlatie tussen verschillende sectoren.