Hoe z-scores in excel te berekenen

In de statistiek vertelt een z-score ons hoeveel standaarddeviaties een waarde afwijkt van het gemiddelde . We gebruiken de volgende formule om een z-score te berekenen:

z = (X – μ) / σ

Goud:

• X is een enkele onbewerkte gegevenswaarde
• μ is het gemiddelde van de dataset
• σ is de standaardafwijking van de dataset

In deze tutorial wordt uitgelegd hoe u z-scores voor onbewerkte gegevenswaarden in Excel kunt berekenen.

Hoe Z-scores in Excel te berekenen

Stel dat we de volgende gegevensset hebben en de z-score voor elke ruwe gegevenswaarde willen vinden:

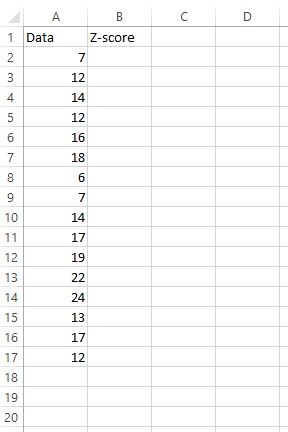
Hiervoor kunnen we de volgende stappen uitvoeren.

Stap 1: Zoek het gemiddelde en de standaardafwijking van de dataset.

Eerst moeten we het gemiddelde en de standaarddeviatie van de dataset vinden. De volgende formules laten zien hoe u dit doet:

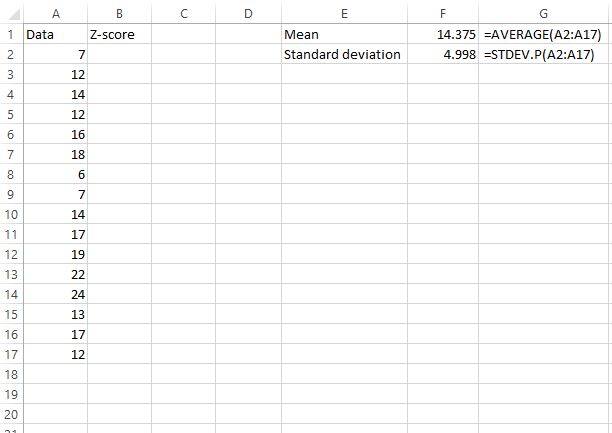
Het gemiddelde blijkt 14,375 te zijn en de standaarddeviatie is 4,998 .

Stap 2: Zoek de z-score voor de eerste ruwe gegevenswaarde.

Vervolgens vinden we de z-score voor de eerste ruwe gegevenswaarde met behulp van de formule z = (X – μ) / σ.

Cel C2 toont de formule die we hebben gebruikt om de z-waarde in cel B2 te berekenen.

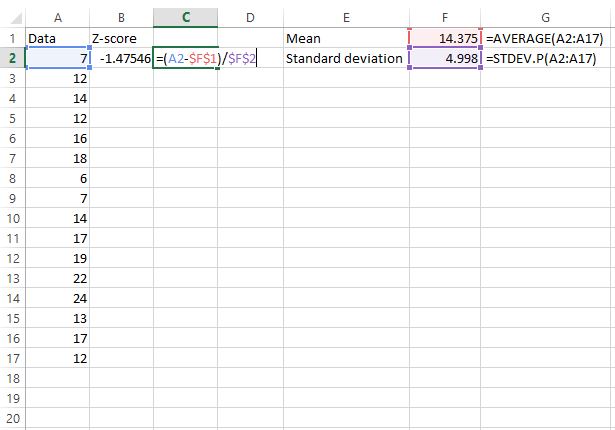
Stap 3: Zoek de z-scores voor alle resterende waarden.

Nu we de z-score voor de eerste waarde in de gegevensset hebben gevonden, kunnen we eenvoudig de formule die we in cel B2 hebben gebruikt, kopiëren naar de rest van de gegevenswaarden. We kunnen dit doen door de volledige z-score-kolom te markeren, te beginnen met de eerste z-score die we al hebben berekend:

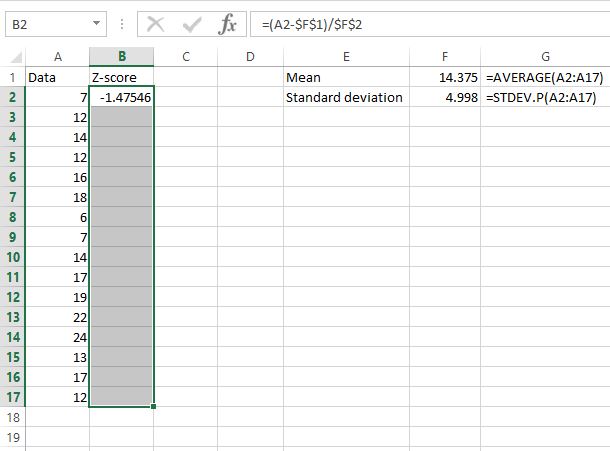
Druk vervolgens op Ctrl+D . Hiermee kopieert u de formule van de eerste cel naar alle cellen eronder.

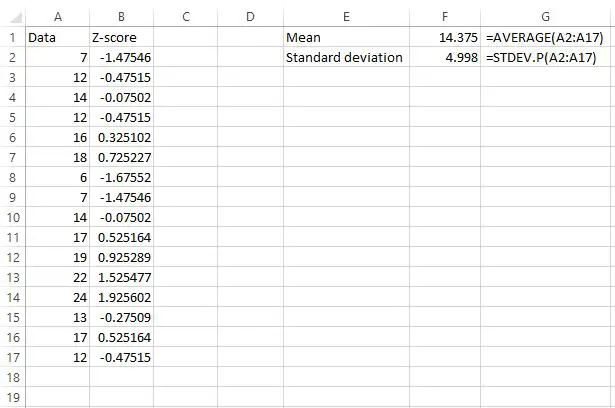
We hebben nu de z-score voor elke ruwe gegevenswaarde gevonden.

Hoe Z-scores in Excel te interpreteren

Bedenk dat een z-score ons eenvoudigweg vertelt hoeveel standaarddeviaties een waarde van het gemiddelde afwijkt.

Een z-score kan positief, negatief of nul zijn.

Een positieve z-score geeft aan dat een bepaalde waarde boven het gemiddelde ligt, een negatieve z-score geeft aan dat een bepaalde waarde onder het gemiddelde ligt, en een z-score van nul geeft aan dat een bepaalde waarde gelijk is aan het gemiddelde.

In ons voorbeeld ontdekten we dat het gemiddelde 14,375 was en de standaarddeviatie 4,998 .

De eerste waarde in onze dataset was dus 7, die een z-score had van (7-14.375) / 4.998 = -1.47546 . Dit betekent dat de waarde “7” -1,47545 standaarddeviaties lager is dan het gemiddelde.

De volgende waarde in onze gegevens, 12, had een z-score van (12-14.375) / 4.998 = -0.47515 . Dit betekent dat de waarde „12“ -0,47515 standaardafwijkingen lager is dan het gemiddelde.

Hoe verder een waarde van het gemiddelde verwijderd is, hoe hoger de absolute waarde van de z-score voor die waarde zal zijn.

De waarde 7 ligt bijvoorbeeld verder van het gemiddelde (14,375) dan de waarde 12, wat verklaart waarom 7 een z-score had met een grotere absolute waarde.

Aanvullende bronnen

De volgende artikelen bieden aanvullende informatie over het werken met z-scores in Excel:

Hoe u een P-waarde kunt vinden uit een Z-score in Excel
Hoe te converteren tussen Z-scores en percentielen in Excel