Hoe een correlatiematrix te lezen

In de statistiek proberen we vaak de relatie tussen twee variabelen te begrijpen.

We willen bijvoorbeeld inzicht krijgen in de relatie tussen het aantal uren dat een student studeert en het cijfer dat hij of zij voor het examen krijgt.

Eén manier om deze relatie te kwantificeren is door de Pearson-correlatiecoëfficiënt te gebruiken, die een maatstaf is voor de lineaire associatie tussen twee variabelen . Het heeft een waarde tussen -1 en 1 waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

Hoe verder de correlatiecoëfficiënt van nul verwijderd is, hoe sterker de relatie tussen de twee variabelen.

Gerelateerd: Wat wordt beschouwd als een “sterke” correlatie?

Maar in sommige gevallen willen we de correlatie tussen meerdere paren variabelen begrijpen. In deze gevallen kunnen we een correlatiematrix maken, een vierkante tabel die de correlatiecoëfficiënten tussen verschillende variabelen weergeeft.

Voorbeeld van een correlatiematrix

De onderstaande correlatiematrix geeft de correlatiecoëfficiënten weer tussen verschillende onderwijsgerelateerde variabelen:

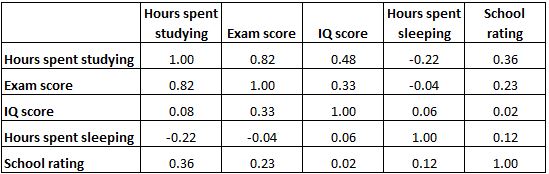
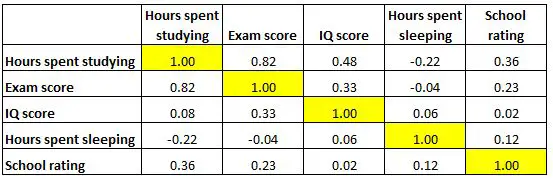
Elke cel in de tabel toont de correlatie tussen twee specifieke variabelen. Uit de gemarkeerde cel hieronder blijkt bijvoorbeeld dat de correlatie tussen ‚uren besteed aan studeren‘ en ‚examencijfer‘ 0,82 bedraagt, wat aangeeft dat deze sterk positief gecorreleerd zijn. Meer uren studeren hangen nauw samen met hogere examenscores.

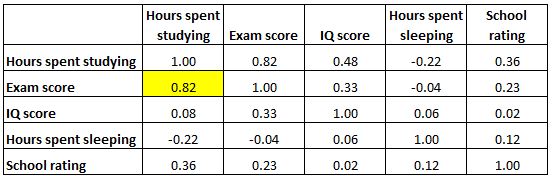
En de gemarkeerde cel hieronder laat zien dat de correlatie tussen ‚uren besteed aan studeren‘ en ‚uren besteed aan slapen‘ -0,22 is, wat aangeeft dat ze zwak negatief gecorreleerd zijn. Meer uren studeren gaan gepaard met minder uren slapen.

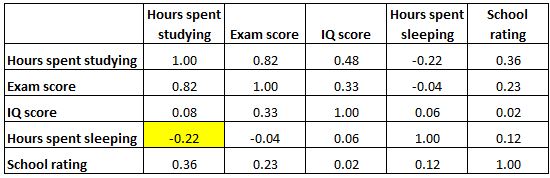
En de gemarkeerde cel hieronder laat zien dat de correlatie tussen ‚uren besteed aan slapen‘ en ‚IQ-score‘ 0,06 is, wat aangeeft dat ze in principe niet gecorreleerd zijn. Er is zeer weinig verband tussen het aantal uren dat een student slaapt en zijn IQ-score.

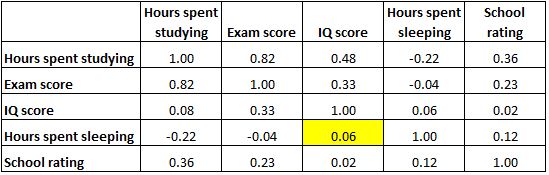
Merk ook op dat de correlatiecoëfficiënten langs de diagonaal van de tabel allemaal gelijk zijn aan 1, omdat elke variabele perfect gecorreleerd is met zichzelf. Deze cellen zijn niet bruikbaar voor interpretatie.

Variaties van de correlatiematrix

Merk op dat een correlatiematrix perfect symmetrisch is. De cel rechtsboven toont bijvoorbeeld exact dezelfde waarde als de cel linksonder:

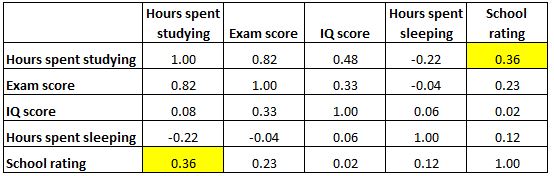
De twee cellen meten inderdaad de correlatie tussen ‘uren besteed aan studeren’ en ‘schoolcijfer’.

Omdat een correlatiematrix symmetrisch is, is de helft van de correlatiecoëfficiënten die in de matrix worden weergegeven overbodig en onnodig. Soms wordt dus slechts de helft van de correlatiematrix weergegeven:

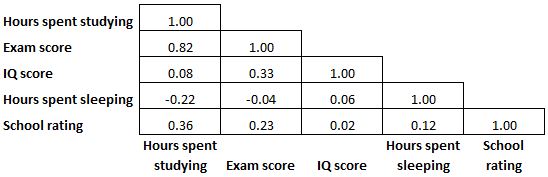
En soms wordt een correlatiematrix gekleurd als een hittekaart om de correlatiecoëfficiënten nog gemakkelijker leesbaar te maken:

Wanneer moet u een correlatiematrix gebruiken?

In de praktijk wordt een correlatiematrix vaak gebruikt om drie redenen:

1. Een correlatiematrix vat op handige wijze een reeks gegevens samen.

Een correlatiematrix is een eenvoudige manier om de correlaties tussen alle variabelen in een dataset samen te vatten. Stel dat we bijvoorbeeld de volgende dataset hebben met de volgende informatie voor 1000 studenten:

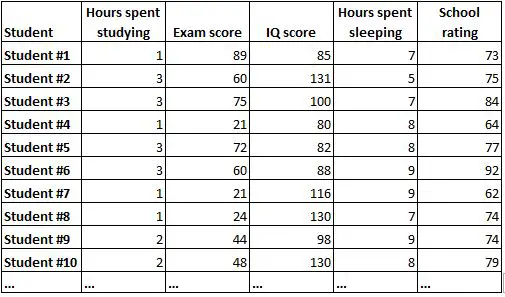
Het zou heel moeilijk zijn om de relatie tussen elke variabele te begrijpen door alleen maar naar de ruwe gegevens te kijken. Gelukkig kan een correlatiematrix ons helpen de correlaties tussen elk paar variabelen snel te begrijpen.

2. Een correlatiematrix dient als diagnose voor de regressie.

Een van de belangrijkste aannames van meervoudige lineaire regressie is dat geen enkele onafhankelijke variabele in het model sterk gecorreleerd is met enige andere variabele in het model.

Wanneer twee onafhankelijke variabelen sterk gecorreleerd zijn, resulteert dit in een probleem dat multicollineariteit wordt genoemd en kan het moeilijk maken om regressieresultaten te interpreteren.

Een van de eenvoudigste manieren om een potentieel multicollineariteitsprobleem op te sporen, is door naar een correlatiematrix te kijken en visueel te controleren of een van de variabelen sterk met elkaar gecorreleerd is.

3. Een correlatiematrix kan gebruikt worden als input voor andere analyses.

Een correlatiematrix wordt gebruikt als input voor andere complexe analyses zoals verkennende factoranalyse en structurele vergelijkingsmodellen.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u een correlatiematrix maakt met behulp van verschillende statistische software:

Hoe u een correlatiematrix maakt in Excel
Hoe u een correlatiematrix maakt in SPSS
Hoe u een correlatiematrix maakt in Stata
Hoe u een correlatiematrix in Python maakt