Hoe het interkwartielbereik (iqr) in excel te berekenen

In deze zelfstudie wordt uitgelegd hoe u het interkwartielbereik van een gegevensset in Excel kunt berekenen.

Wat is de interkwartielafstand?

Het interkwartielbereik , vaak IQR genoemd, is een manier om de verdeling van de middelste 50% van een dataset te meten. Het wordt berekend als het verschil tussen het eerste kwartiel* (Q1) en het derde kwartiel (Q3) van een dataset.

*Kwartielen zijn eenvoudigweg waarden die een dataset in vier gelijke delen verdelen.

Stel dat we bijvoorbeeld de volgende gegevensset hebben:

[58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98]

Het derde kwartiel blijkt 91 te zijn en het eerste kwartiel 75,5 . Het interkwartielbereik (IQR) voor deze dataset is dus 91 – 75,5 = 15 . Dit vertelt ons de verdeling van de middelste 50% van de waarden in deze dataset.

Hoe het interkwartielbereik in Excel te berekenen

Microsoft Excel heeft geen ingebouwde functie om de IQR van een dataset te berekenen, maar we kunnen deze eenvoudig vinden met behulp van de QUARTILE()- functie, die de volgende argumenten nodig heeft:

KWARTIEL(matrix; kwartaal)

• array: de gegevensarray waarin u geïnteresseerd bent.
• kwartiel: het kwartiel dat u wilt berekenen.

Voorbeeld: zoeken naar IQR in Excel

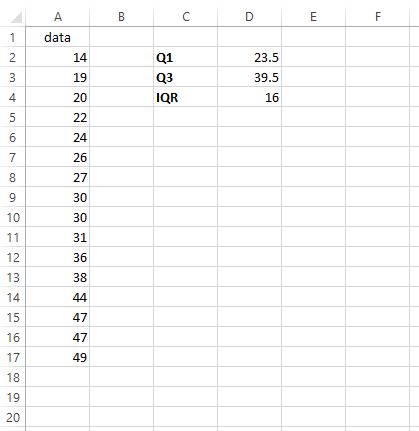
Stel dat we de IQR willen vinden voor de volgende dataset:

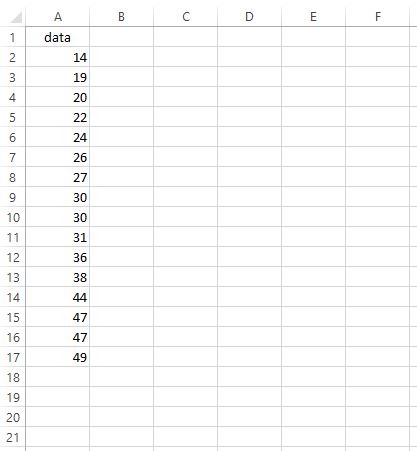
Om de IQR te vinden, kunnen we de volgende stappen uitvoeren:

Stap 1: Zoek naar Q1 .

Om het eerste kwartiel te vinden, typen we eenvoudigweg =QUARTILE(A2:A17, 1) in elke gewenste cel:

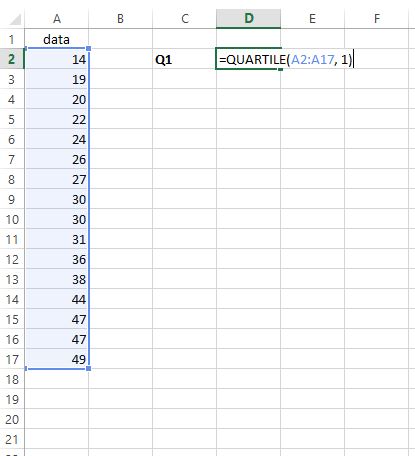
Stap 2: Zoek naar Q3 .

Om het derde kwartiel te vinden, typen we =QUARTILE(A2:A17, 3) in elke gewenste cel:

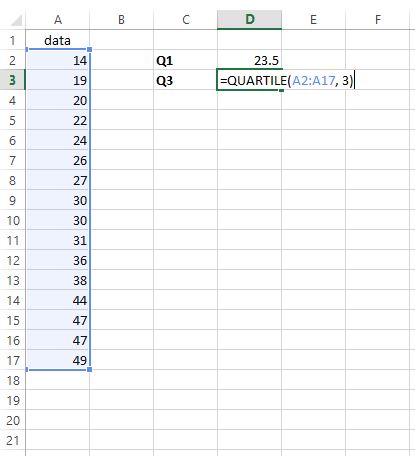
Stap 3: Zoek IQR .

Om de interkwartielafstand (IQR) te vinden, trekken we eenvoudigweg Q1 af van Q3:

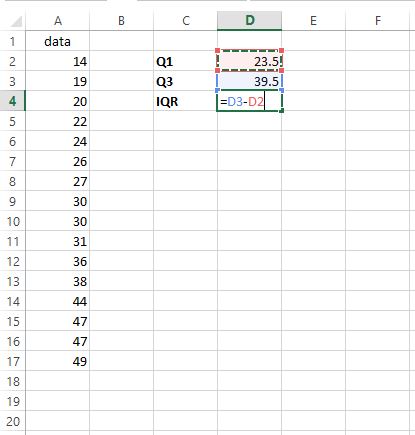
De IQR blijkt 39,5 – 23,5 = 16 te zijn. Dit vertelt ons hoe verdeeld de middelste 50% van de waarden in deze specifieke dataset zijn.

Een kortere aanpak

Merk op dat we in het vorige voorbeeld ook het interkwartielbereik van de dataset hadden kunnen vinden met behulp van een formule:

=KWARTIEL(A2:A17, 3) – KWARTIEL(A2:A17, 1)

Dit zou ook de waarde 16 opleveren.

Conclusie

Het interkwartielbereik is slechts één manier om de ‘spreiding’ van een dataset te meten. Andere manieren om de spreiding te meten zijn bereik, standaarddeviatie en variantie.

Het voordeel van het gebruik van IQR om de spread te meten is dat het robuust is voor uitschieters . Omdat het ons alleen de verdeling van de middelste 50% van de dataset vertelt, wordt het niet beïnvloed door ongewoon kleine of ongewoon grote uitschieters.

Dit maakt het een betere manier om spreiding te meten dan een metriekachtig bereik, dat ons eenvoudigweg het verschil vertelt tussen de grootste en kleinste waarden in een dataset.

Gerelateerd: Hoe u het middenbereik in Excel kunt berekenen