Een eenvoudige uitleg van continuïteitscorrectie in statistieken
Continuïteitscorrectie wordt toegepast als u een continue verdeling wilt gebruiken om een discrete verdeling te benaderen. Over het algemeen wordt het gebruikt als u een normale verdeling wilt gebruiken om een binominale verdeling te benaderen.
Bedenk dat de binominale verdeling ons de waarschijnlijkheid vertelt van het behalen van x succes in n pogingen, gegeven het feit dat de kans op succes in een enkele poging p is. Om vragen over waarschijnlijkheid met een binomiale verdeling te beantwoorden, kunnen we eenvoudigweg een binomiale verdelingscalculator gebruiken, maar we kunnen de waarschijnlijkheid ook benaderen met behulp van een normale verdeling met een continuïteitscorrectie.
Een continuïteitscorrectie is de naam die wordt gegeven aan het optellen of aftrekken van 0,5 bij een discrete x-waarde .
Laten we bijvoorbeeld zeggen dat we de waarschijnlijkheid willen bepalen dat een munt in de loop van 100 worpen 45 keer op kop zal landen die minder dan of gelijk is aan 45 keer. Dat wil zeggen, we willen P(X ≤ 45) vinden. Om de normale verdeling te gebruiken om de binominale verdeling te benaderen, zouden we in plaats daarvan P(X ≤ 45,5) vinden.
De volgende tabel laat zien wanneer je 0,5 moet optellen of aftrekken, afhankelijk van het type waarschijnlijkheid dat je probeert te vinden:
| Gebruik de binominale verdeling | Gebruik van de normale verdeling met continuïteitscorrectie |
|---|---|
| X = 45 | 44,5<X<45,5 |
| X ≤ 45 | X<45,5 |
| X<45 | X<44,5 |
| X ≥ 45 | X > 44,5 |
| X > 45 | X > 45,5 |
Opmerking:
Het is alleen passend om een continuïteitscorrectie op de normale verdeling toe te passen om de binomiale verdeling te benaderen wanneer n*p en n*(1-p) beide minstens 5 zijn.
Stel bijvoorbeeld dat n = 15 en p = 0,6. In dit geval:
n*p = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Aangezien beide getallen groter dan of gelijk zijn aan 5, zou het acceptabel zijn om in dit scenario een continuïteitscorrectie toe te passen.
Het volgende voorbeeld illustreert hoe u een continuïteitscorrectie op de normale verdeling kunt toepassen om de binominale verdeling te benaderen.
Voorbeeld van toepassing van continuïteitscorrectie
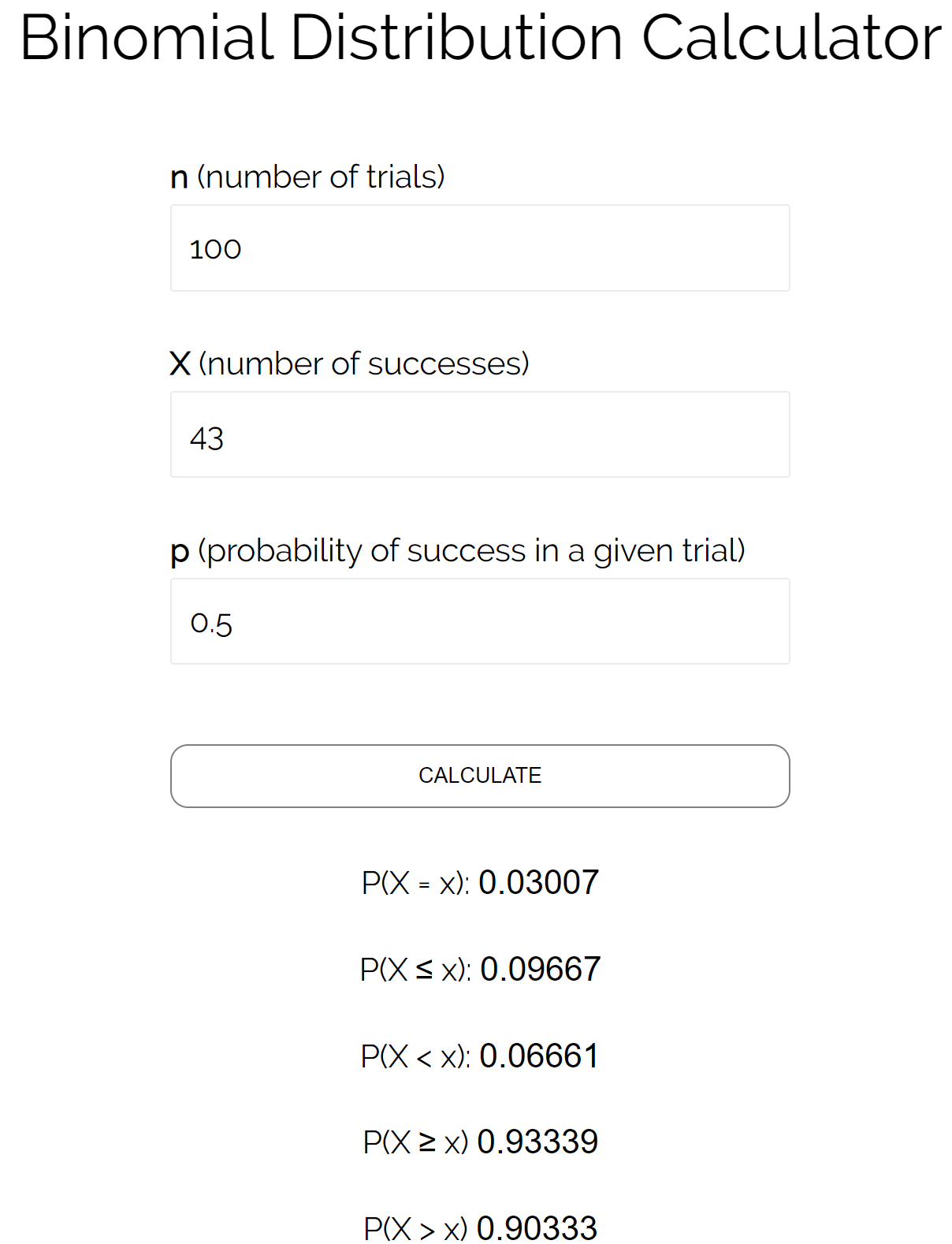
Stel dat we de waarschijnlijkheid willen weten dat een munt bij 100 worpen minder dan of gelijk aan 43 keer op kop zal landen. In dit geval:
n = aantal pogingen = 100
X = aantal successen = 43
p = kans op succes in een bepaalde proef = 0,50
We kunnen deze getallen in de binomiale verdelingscalculator pluggen om te zien dat de kans dat de munt op kop kleiner dan of gelijk aan 43 keer terechtkomt, 0,09667 is.
Om de binomiale verdeling te benaderen door een continuïteitscorrectie toe te passen op de normale verdeling, kunnen we de volgende stappen gebruiken:
Stap 1: Controleer of n*p en n*(1-p) beide minimaal 5 zijn .
n*p = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Beide getallen zijn groter dan of gelijk aan 5, dus we kunnen doorgaan.
Stap 2: Bepaal of u 0,5 moet optellen of aftrekken
Als we naar de bovenstaande tabel verwijzen, zien we dat we 0,5 moeten optellen als we met waarschijnlijkheid werken in de vorm van X ≤ 43. We zullen dus P(X< 43,5) vinden.
Stap 3: Zoek het gemiddelde (μ) en de standaardafwijking (σ) van de binominale verdeling.
µ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
Stap 4: Vind de z-score met behulp van het gemiddelde en de standaardafwijking die u in de vorige stap hebt gevonden.
z = (x – μ) / σ = (43,5 – 50) / 5 = -6,5 / 5 = -1,3.
Stap 5: Gebruik de Z-tabel om de waarschijnlijkheid te vinden die verband houdt met de z-score.
Volgens Tabel Z is de waarschijnlijkheid geassocieerd met z = -1,3 0,0968 .
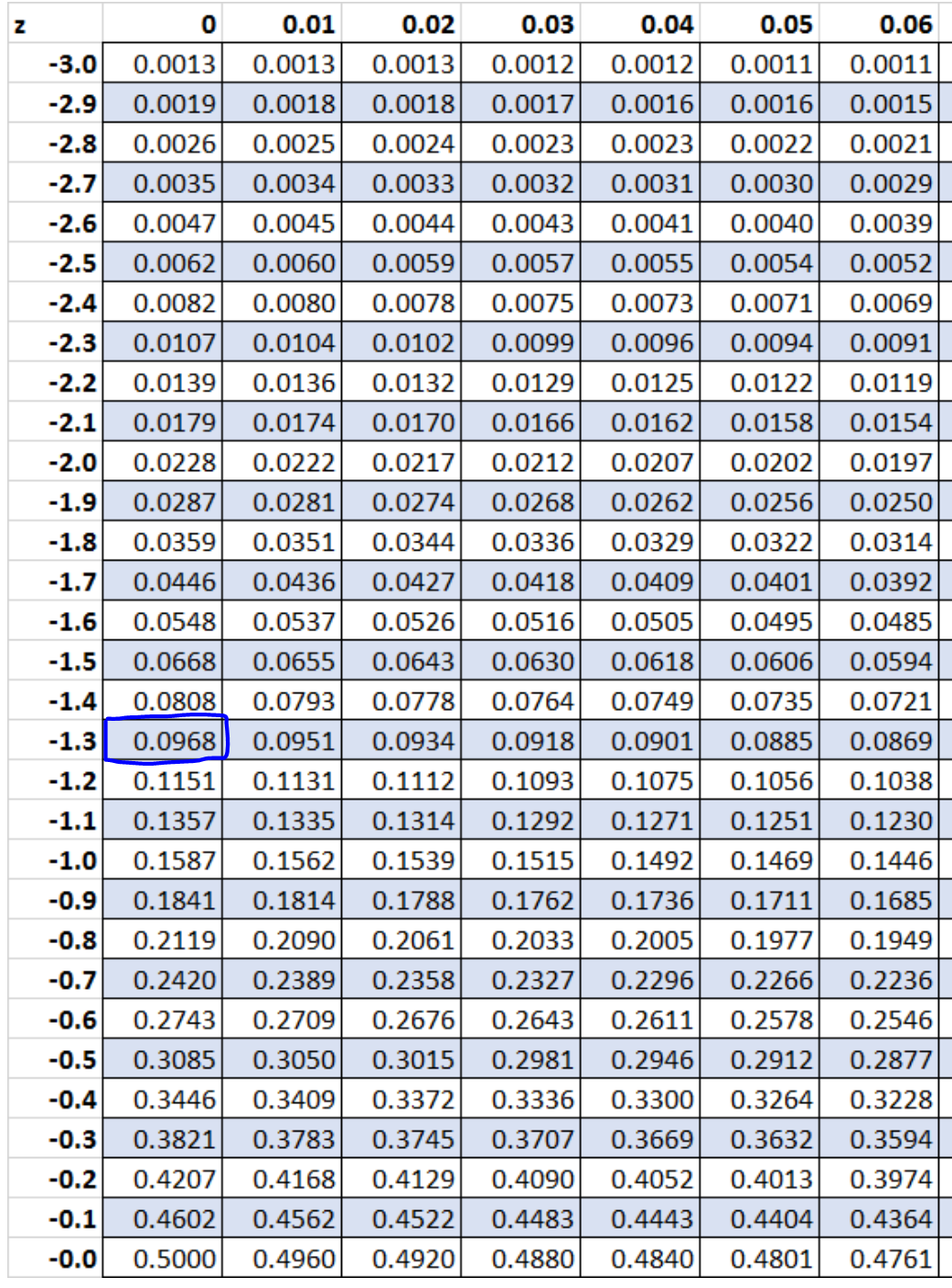
Dus de exacte waarschijnlijkheid die we vonden met behulp van de binomiale verdeling was 0,09667 , terwijl de geschatte waarschijnlijkheid die we vonden met behulp van de continuïteitscorrectie met de normale verdeling 0,0968 was. Deze twee waarden zijn behoorlijk gesloten.
Wanneer moet u continuïteitscorrectie gebruiken?
Voordat moderne statistische software bestond en berekeningen handmatig moesten worden uitgevoerd, werden continuïteitscorrecties vaak gebruikt om kansen te vinden met betrekking tot discrete verdelingen. Tegenwoordig spelen continuïteitscorrecties een minder grote rol bij het berekenen van kansen, omdat we meestal kunnen vertrouwen op software of rekenmachines om kansen voor ons te berekenen.
In plaats daarvan is het eenvoudigweg een onderwerp dat in statistiekcursussen wordt behandeld om de relatie tussen een binomiale verdeling en een normale verdeling te illustreren en om aan te tonen dat het mogelijk is dat een normale verdeling een binomiale verdeling benadert door een continuïteitscorrectie toe te passen.
Continuïteitscorrectiecalculator
Gebruik de continuïteitscorrectiecalculator om automatisch een continuïteitscorrectie toe te passen op een normale verdeling om binomiale kansen te benaderen.