Hoe u een mann-kendall-trendtest uitvoert in r

Om te bepalen of er al dan niet sprake is van een trend in tijdreeksgegevens, wordt een Mann-Kendall-trendtest gebruikt. Dit is een niet-parametrische test, wat betekent dat er geen onderliggende aannames worden gedaan over de normaliteit van de gegevens.

De testhypotheses zijn als volgt:

H ₀ (nulhypothese): er is geen trend aanwezig in de gegevens.

H _A (alternatieve hypothese): Er is een trend aanwezig in de gegevens. (Dit kan een positieve of negatieve trend zijn)

Als de p-waarde van de test onder een bepaald significantieniveau ligt (veel voorkomende keuzes zijn 0,10, 0,05 en 0,01), dan is er statistisch significant bewijs dat er een trend aanwezig is in de gegevens uit de tijdreeks.

In deze tutorial wordt uitgelegd hoe u een Mann-Kendall-trendtest uitvoert in R.

Voorbeeld: Mann-Kendall-trendtest in R

Om een Mann-Kendall-trendtest in R uit te voeren, gebruiken we de MannKendall()- functie uit de Kendall- bibliotheek, die de volgende syntaxis gebruikt:

MannKendall(x)

Goud:

• x = een gegevensvector, vaak een tijdreeks

Om te illustreren hoe de test moet worden uitgevoerd, zullen we de ingebouwde PrecipGL- dataset van de Kendall Library gebruiken, die jaarlijkse neerslaginformatie bevat voor alle Grote Meren van 1900 tot 1986:

 #load Kendall library and PrecipGL dataset
library(Kendall)
data(PrecipGL)

#view dataset
PrecipGL

Time Series:
Start = 1900 
End = 1986 
Frequency = 1 
[1] 31.69 29.77 31.70 33.06 31.31 32.72 31.18 29.90 29.17 31.48 28.11 32.61
[13] 31.31 30.96 28.40 30.68 33.67 28.65 30.62 30.21 28.79 30.92 30.92 28.13
[25] 30.51 27.63 34.80 32.10 33.86 32.33 25.69 30.60 32.85 30.31 27.71 30.34
[37] 29.14 33.41 33.51 29.90 32.69 32.34 35.01 33.05 31.15 36.36 29.83 33.70
[49] 29.81 32.41 35.90 37.45 30.39 31.15 35.75 31.14 30.06 32.40 28.44 36.38
[61] 31.73 31.27 28.51 26.01 31.27 35.57 30.85 33.35 35.82 31.78 34.25 31.43
[73] 35.97 33.87 28.94 34.62 31.06 38.84 32.25 35.86 32.93 32.69 34.39 33.97
[85] 32.15 40.16 36.32
attr(,"title")
[1] Annual precipitation, 1900-1986, Entire Great Lakes

Om te zien of er een trend in de gegevens zit, kunnen we de Mann-Kendall-trendtest uitvoeren:

 #Perform the Mann-Kendall Trend Test
MannKendall(PrecipGL)

tau = 0.265, 2-sided pvalue = 0.00029206

De teststatistiek is 0,265 en de overeenkomstige tweezijdige p-waarde is 0,00029206 . Omdat deze p-waarde kleiner is dan 0,05, zullen we de nulhypothese van de test verwerpen en concluderen dat er een trend aanwezig is in de gegevens.

Om de trend te visualiseren, kunnen we een tijdgrafiek van de jaarlijkse neerslag per jaar maken en een vloeiende lijn toevoegen om de trend weer te geven:

 #Plot the time series data
plot(PrecipGL)

#Add a smooth line to visualize the trend 
lines(lowess(time(PrecipGL),PrecipGL), col='blue')

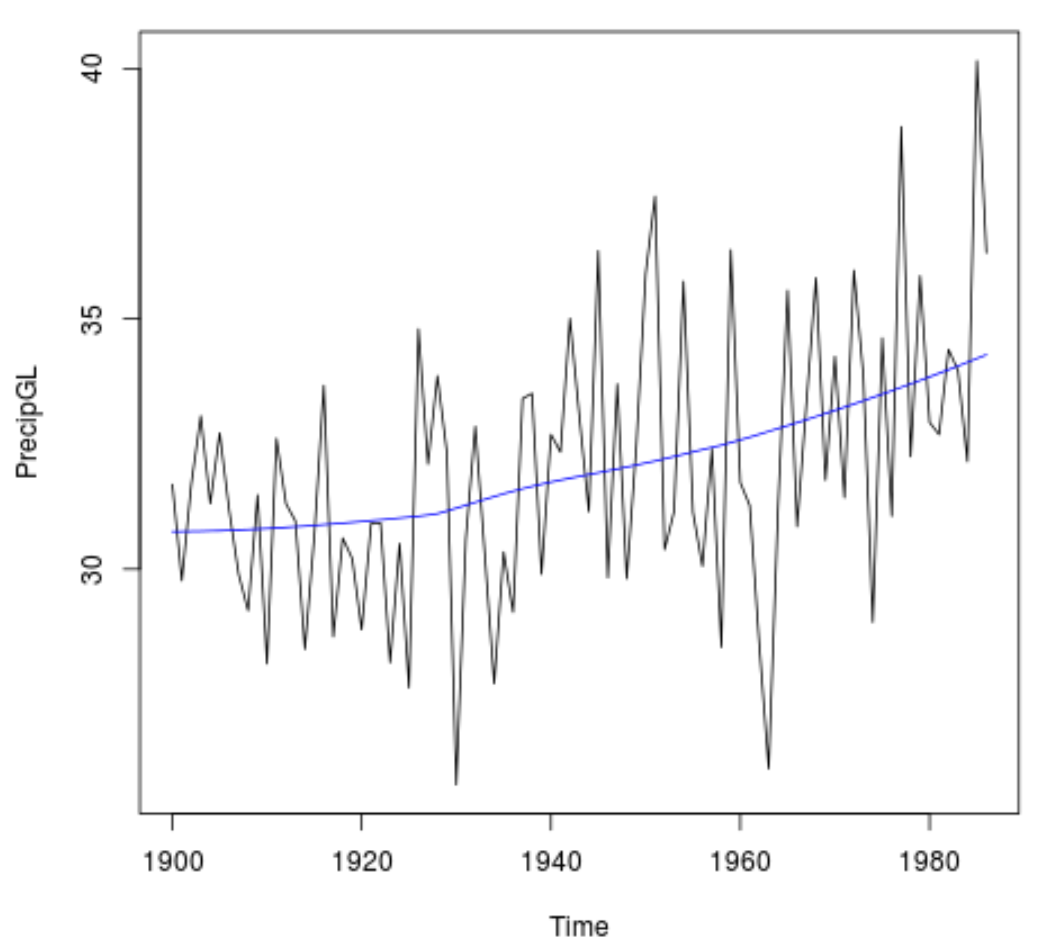
Merk op dat we ook een seizoensgecorrigeerde Mann-Kendall-trendtest kunnen uitvoeren om rekening te houden met eventuele seizoensinvloeden in de gegevens met behulp van de opdracht SeasonalMannKendall(x) :

 #Perform a seasonally-adjusted Mann-Kendall Trend Test
SeasonalMannKendall(PrecipGL)

tau = 0.265, 2-sided pvalue = 0.00028797

De teststatistiek is 0,265 en de overeenkomstige tweezijdige p-waarde is 0,00028797 . Opnieuw is deze p-waarde kleiner dan 0,05, dus we zullen de nulhypothese van de test verwerpen en concluderen dat er een trend aanwezig is in de gegevens.