Deciel

Von Dr.benjamin anderson August 5, 2023 Statistieken Keine Kommentare

In dit artikel leggen we uit wat decielen zijn en hoe ze worden berekend. U vindt er ook verschillende opgeloste stapsgewijze voorbeelden van decielberekeningen en bovendien kunt u de decielen van elke statistische steekproef berekenen met een online rekenmachine.

Wat zijn decielen?

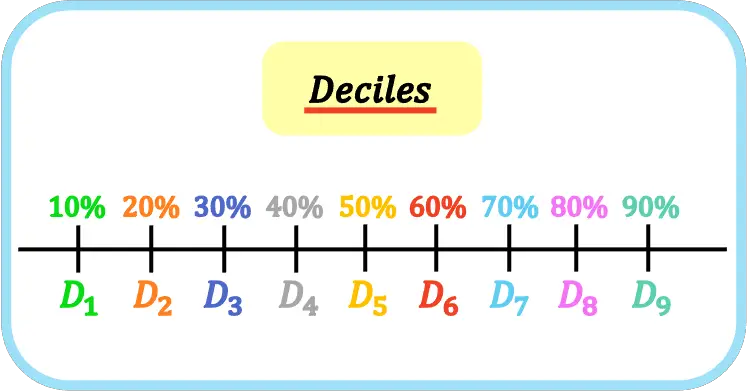
In de statistieken zijn decielen de negen waarden die een reeks geordende gegevens in tien gelijke delen verdelen. Zodat het eerste, tweede, derde,… deciel 10%, 20%, 30%,… van de steekproef of populatie vertegenwoordigt.

De waarde van het vierde deciel is bijvoorbeeld hoger dan 40% van de gegevens, maar lager dan de rest van de gegevens.

Decielen worden weergegeven door de hoofdletter D en de decielindex, dat wil zeggen, het eerste deciel is D ₁ , het tweede deciel is D ₂ , het derde deciel is D ₃ , enz.

👉 U kunt de onderstaande rekenmachine gebruiken om decielen voor elke dataset te berekenen.

Opgemerkt moet worden dat decielen op dezelfde manier een maatstaf zijn voor de niet-centrale positie als kwartielen, kwintielen en percentielen. U kunt de betekenis van elk van deze kwantieltypen op onze website controleren.

Bovendien is het vijfde deciel gelijk aan de mediaan en het tweede kwartiel, aangezien ze de gehele gegevensset in twee gelijke delen verdelen.

Hoe decielen te berekenen

Om de decielpositie van een reeks statistische gegevens te berekenen , vermenigvuldigt u het decielgetal met de som van het totale aantal gegevens plus één en deelt u het resultaat door tien.

De decielformule is daarom:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Let op: deze formule vertelt ons de positie van het deciel, niet de waarde van het deciel. Het deciel bestaat uit de gegevens die zich bevinden op de positie die door de formule wordt verkregen.

Soms geeft het resultaat van deze formule ons echter een decimaal getal. We moeten daarom twee gevallen onderscheiden, afhankelijk van of het resultaat een decimaal getal is of niet:

Als het resultaat van de formule een getal is zonder een decimaal deel , bestaat het deciel uit de gegevens die zich bevinden op de positie die wordt geboden door de bovenstaande formule.
Als het resultaat van de formule een getal met een decimaal deel is, wordt de decielwaarde berekend met behulp van de volgende formule:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Waar x _i en x _i+1 de getallen zijn van de posities waartussen het getal verkregen door de eerste formule zich bevindt, en d het decimale deel is van het getal verkregen door de eerste formule.

Nu zou je kunnen denken dat het verkrijgen van de decielen van een statistische steekproef complex is, maar in de praktijk is het vrij eenvoudig. Als u de volgende twee voorbeelden leest, zult u het zeker veel beter begrijpen.

Opmerking : de wetenschappelijke gemeenschap is het niet helemaal eens over de manier waarop decielen moeten worden berekend, dus er zijn statistiekboeken te vinden die het iets anders uitleggen.

Voorbeeld van decielberekening

Zoals je hierboven hebt gezien, hangt de berekening van decielen af van het feit of het getal dat de eerste formule ons geeft decimaal is of niet. Daarom hebben we hieronder twee opgeloste voorbeelden opgesteld, één voor elk geval. Bedenk in ieder geval dat als u vragen heeft over de samenstelling van de decielen, u deze in de opmerkingen kunt stellen.

voorbeeld 1

Gegeven de volgende gegevens, van klein naar groot, vind je het eerste, derde en achtste deciel van de steekproef.

De gegevens in deze oefening zijn al gesorteerd, dus het is niet nodig om de volgorde te wijzigen, anders zouden we de gegevens eerst van klein naar groot moeten sorteren.

Zoals hierboven uitgelegd, is de formule die het mogelijk maakt om de posities van de decielen te vinden als volgt:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

De steekproefgrootte voor deze oefening is 29 waarnemingen, dus om de positie van het eerste deciel te berekenen, moet je 29 vervangen door n en 1 door k :

$\cfrac{1\cdot (29+1)}{10}=3\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_1=85$

Het resultaat van de formule is 3, dus het eerste deciel staat op de derde positie van de geordende lijst, en deze waarde komt overeen met 85.

Nu passen we dezelfde procedure opnieuw toe, maar dan met het derde deciel. We gebruiken de formule waarbij we de k vervangen door een 3:

$\cfrac{3\cdot (29+1)}{10}=9\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_3=97$

Het derde deciel zal dus het element zijn dat op de negende plaats staat, namelijk 97.

Ten slotte doen we hetzelfde proces, maar plaatsen we een 8 in de formule om het achtste deciel te bepalen:

$\cfrac{8\cdot (29+1)}{10}=24\quad \color{orange}\bm{\longrightarrow}\color{black}\quad D_8=131$

Het achtste deciel is het nummer op positie 24 van de geordende datalijst, dus het achtste deciel is 131.

Voorbeeld 2

Bereken uit de gegevens in de volgende tabel decielen 4, 7 en 9.

Om de posities van de decielen te verkrijgen, moet u, net als in het vorige voorbeeld, de volgende formule gebruiken:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1,2,3,4,5,6,7,8,9$

In dit geval is de steekproefomvang 42, dus om de positie van het vierde deciel te vinden moet je de parameter n vervangen door 42 en de k door 4:

$\cfrac{4\cdot (42+1)}{10}=17,2$

Maar deze keer hebben we een decimaal getal uit de formule gehaald, dus moeten we de volgende formule toepassen om het exacte deciel te berekenen:

$D=x_i+d\cdot (x_{i+1}-x_i)$

Het getal verkregen uit de eerste formule is 17,2, dus het vierde deciel ligt tussen het zeventiende en achttiende gegeven, respectievelijk 109 en 112. Daarom is x _i 109, x _{i+ 1} is 112 en d is het decimale deel. van het verkregen aantal, namelijk 0,2.

$D_4=109+0,2\cdot (112-109)=109,6$

We herhalen hetzelfde proces om het zevende deciel te vinden. We berekenen eerst de positie van het deciel:

$\cfrac{7\cdot (42+1)}{10}=30,1$

Uit de formule hebben we het getal 30.1 verkregen, wat betekent dat het deciel tussen de posities 30 en 31 zal liggen, waarvan de waarden 154 en 159 zijn. De berekening van het exacte deciel is daarom:

$D_7=154+0,1\cdot (159-154)=154,5$

Tenslotte passen we dezelfde methode opnieuw toe om het negende deciel te verkrijgen. We bepalen de positie van het deciel:

$\cfrac{9\cdot (42+1)}{10}=38,7$

Het verkregen getal is decimaal en ligt tussen 38 en 39, waarvan de posities overeenkomen met de waarden 189 en 196. De berekening van deciel 9 is dus:

$D_9=189+0,7\cdot (196-189)=193,9$

Deciel rekenmachine

Sluit een statistische gegevensset aan op de onderstaande rekenmachine om decielen te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Decielen in gegroepeerde gegevens

Om decielen te berekenen wanneer gegevens in intervallen zijn gegroepeerd , moeten we eerst het interval of de bak vinden waarin het deciel valt met behulp van de volgende formule:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,3,4,5,6,7,8,9$

Het deciel zal zich daarom in het interval bevinden waarvan de absolute frequentie onmiddellijk groter is dan het getal verkregen in de vorige uitdrukking.

En zodra we al weten tot welk interval het deciel behoort, moeten we de volgende formule toepassen om de exacte waarde van het deciel te vinden:

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4,5,6,7,8,9$

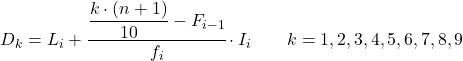
Goud:

_Li is de ondergrens van het interval waarin het deciel zich bevindt.
n is het totale aantal statistische gegevens.
Fi _-1 is de cumulatieve absolute frequentie van het vorige interval.
_fi is de absolute frequentie van het interval waarin het deciel zich bevindt.
I _i is de breedte van het decielinterval.

Om te zien hoe dit in zijn werk gaat, heb je hieronder een ingevulde oefening waarin decielen 3, 5 en 8 van de volgende gegevens, gegroepeerd op intervallen, worden berekend.

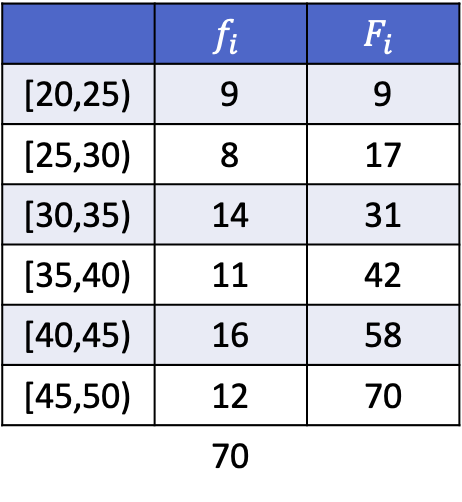
Omdat de gegevens gegroepeerd zijn, bestaat de berekening van elk deciel uit twee stappen: zoek eerst het interval waarin het deciel valt en bereken vervolgens de exacte waarde van het deciel. We vinden daarom het interval van het derde deciel:

$\cfrac{k\cdot (n+1)}{10}$

$\cfrac{3\cdot (70+1)}{10} =21,3 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [30,35)$

Het decielinterval is het interval waarvan de absolute cumulatieve frequentie onmiddellijk groter is dan 21,3, en in dit geval is het het interval [30,35) waarvan de absolute cumulatieve frequentie 31 is. Nu we het decielinterval kennen, passen we de volgende formule toe om te vinden de exacte waarde van het deciel:

$D_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{10}-F_{i-1}}{f_i}\cdot I_i$

$D_3=30+ \cfrac{\displaystyle\frac{3\cdot (70+1)}{10}-17}{14}\cdot 5=31,54$

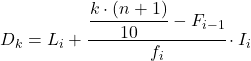
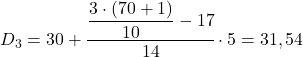
We moeten de methode nu opnieuw toepassen om het vijfde deciel te verkrijgen. We bepalen eerst het interval waarin het ligt:

$\cfrac{5\cdot (70+1)}{10} =35,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [35,40)$

Het resultaat 35 betekent dat het in het interval [35,40) ligt, maar niet omdat er een 35 in de intervaluitdrukking staat, maar omdat de geaccumuleerde absolute frequentie (42) het meest direct hoog is. En zodra het interval is geïdentificeerd, passen we de tweede formule van het proces toe:

$D_5=35+ \cfrac{\displaystyle\frac{5\cdot (70+1)}{10}-31}{11}\cdot 5=37,05$

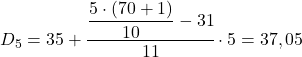
Tenslotte vinden we het achtste deciel. Om dit te doen, berekenen we eerst het interval:

$\cfrac{8\cdot (70+1)}{10} =56,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [40,45)$

De cumulatieve absolute frequentie onmiddellijk boven 56,8 is 58, dus het achtste decielbereik is [40,45). Het is daarom voldoende om de exacte waarde van het deciel te bepalen:

$D_8=40+ \cfrac{\displaystyle\frac{8\cdot (70+1)}{10}-42}{16}\cdot 5=44,63$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder