Een inleiding tot de binominale verdeling

De binomiale verdeling is een van de meest populaire verdelingen in de statistiek. Om de binominale verdeling te begrijpen, helpt het om eerst binominale experimenten te begrijpen.

Binominale experimenten

Een binomiaal experiment is een experiment dat de volgende eigenschappen heeft:

• Het experiment bestaat uit n herhaalde pogingen.
• Elke proef heeft slechts twee mogelijke uitkomsten.
• De kans op succes, aangeduid als p , is voor elke poging hetzelfde.
• Elke test is onafhankelijk.

Het meest voor de hand liggende voorbeeld van een binomiaal experiment is het opgooien van munten. Laten we bijvoorbeeld zeggen dat we een munt 10 keer opgooien. Dit is een binomiaal experiment omdat het de volgende vier eigenschappen heeft:

• Het experiment bestaat uit n herhaalde pogingen – Er zijn 10 pogingen.
• Elke proef heeft slechts twee mogelijke uitkomsten: kop of munt.
• De kans op succes, aangeduid als p , is voor elke poging hetzelfde. Als we ‘succes’ definiëren als landingskoppen, dan is de kans op succes voor elke poging precies 0,5.
• Elke poging is onafhankelijk. Het resultaat van één toss heeft geen invloed op de uitkomst van een andere toss.

De binominale verdeling

De binomiale verdeling beschrijft de waarschijnlijkheid van het behalen van k successen in n binomiale experimenten.

Als een willekeurige variabele X een binominale verdeling volgt, kan de kans dat X = k succes wordt gevonden met de volgende formule:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Goud:

• n: aantal pogingen
• k: aantal successen
• p: kans op succes bij een bepaalde proef
• _n C _k : het aantal manieren om k successen te behalen in n pogingen

Stel dat we bijvoorbeeld drie keer een munt opgooien. We kunnen de bovenstaande formule gebruiken om de kans te bepalen op het krijgen van 0, 1, 2 en 3 kop bij deze 3 worpen:

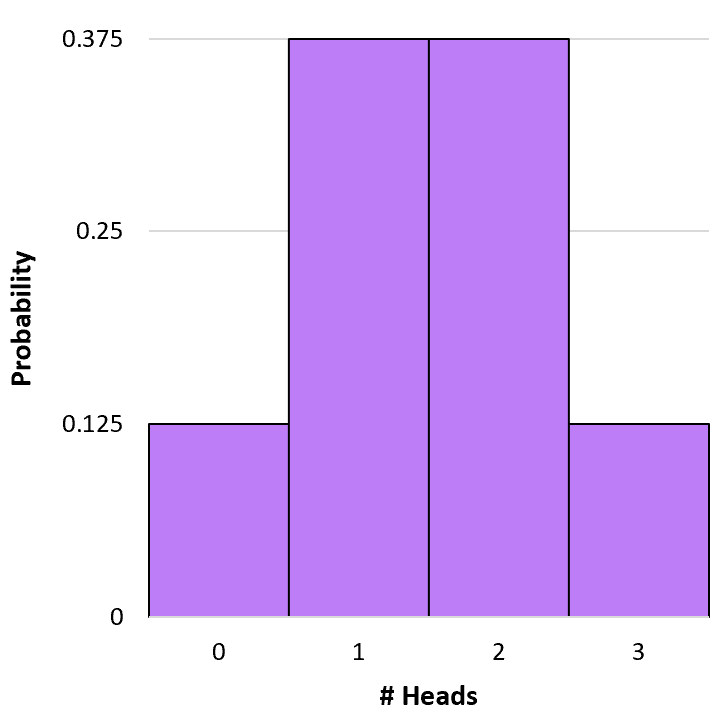
P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 3 * 0,5 * (0,5) ² = 0,375

P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 3 * 0,25 * (0,5) ¹ = 0,375

P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 0,125 * (0,5) ⁰ = 0,125

Opmerking : we hebben deze gecombineerde rekenmachine gebruikt om _{nCk voor} elk voorbeeld te berekenen.

We kunnen een eenvoudig histogram maken om deze waarschijnlijkheidsverdeling te visualiseren:

Berekening van cumulatieve binomiale kansen

Het is eenvoudig om een enkele binomiale waarschijnlijkheid te berekenen (bijvoorbeeld de kans dat een munt 1 keer kop gooit op de 3 worpen) met behulp van de bovenstaande formule, maar om cumulatieve binomiale kansen te berekenen moeten we individuele kansen optellen.

Laten we bijvoorbeeld zeggen dat we de waarschijnlijkheid willen weten dat een munt 1 keer of minder kop krijgt op de 3 worpen. Om deze waarschijnlijkheid te berekenen, gebruiken we de volgende formule:

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

Dit wordt een cumulatieve waarschijnlijkheid genoemd, omdat het gaat om het optellen van meerdere kansen. We kunnen de cumulatieve kans berekenen op het krijgen van k kop of minder voor elke uitkomst met behulp van een vergelijkbare formule:

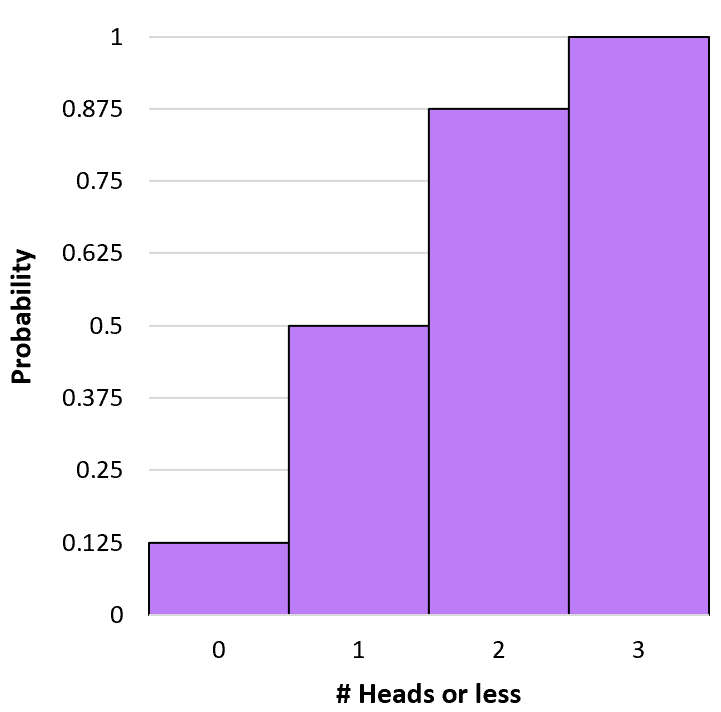
P(X≤0) = P(X=0) = 0,125 .

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .

We kunnen een histogram maken om deze cumulatieve waarschijnlijkheidsverdeling te visualiseren:

Binomiale waarschijnlijkheidscalculator

Als we met kleine getallen werken (bijvoorbeeld drie opgooien), is het redelijk om de binomiale kansen met de hand te berekenen. Wanneer we echter met grotere aantallen werken (bijvoorbeeld 100 trekkingen), kan het lastig zijn om de kansen met de hand te berekenen. In deze gevallen kan het nuttig zijn om een binomiale waarschijnlijkheidscalculator zoals hieronder te gebruiken.

Stel bijvoorbeeld dat we een munt n = 100 keer opgooien, dan is de kans dat deze bij een bepaalde poging op kop terechtkomt p = 0,5, en we willen weten hoe waarschijnlijk het is dat de munt 43 keer of minder op kop landt: k = 43 keer of minder:

Zo interpreteert u het resultaat:

• De kans dat de munt precies 43 keer kop krijgt is 0,03007 .
• De kans dat de munt minder dan 43 keer kop oplevert is 0,06661 .
• De kans dat de munt 43 keer of minder kop oplevert, is 0,09667 .
• De kans dat de munt meer dan 43 keer kop is, is 0,90333 .
• De kans dat de munt 43 keer of vaker kop oplevert, is 0,93339 .

Eigenschappen van de binominale verdeling

De binominale verdeling heeft de volgende eigenschappen:

Het gemiddelde van de verdeling is μ = np

De variantie van de verdeling is σ ² = np(1-p)

De standaardafwijking van de verdeling is σ = √ np(1-p)

Stel dat we bijvoorbeeld drie keer een munt opgooien. Laat p = de kans dat de munt op kop terechtkomt.

Het gemiddelde aantal koppen dat we verwachten is μ = np = 3*.5 = 1.5 .

De variantie in het aantal personen die we verwachten is σ ² = np(1-p) = 3*.5*(1-.5) = 0.75 .

Oefenproblemen met binominale verdeling

Gebruik de volgende oefenproblemen om uw kennis van de binomiale verdeling te testen.

Probleem 1

Vraag: Bob maakt 60% van zijn vrije worppogingen. Als hij twaalf vrije worpen maakt, wat is dan de kans dat hij er precies tien maakt?

Antwoord: Als we de binomiale verdelingscalculator hierboven gebruiken met p = 0,6, n = 12 en k = 10, vinden we dat P(X=10) = 0,06385 .

Probleem 2

Vraag: Jessica gooit 5 keer een muntje op. Wat is de kans dat de munt 2 keer of minder kop krijgt?

Antwoord: Met behulp van de bovenstaande binomiale verdelingscalculator met p = 0,5, n = 5 en k = 2 vinden we dat P(X≤2) = 0,5 .

Probleem 3

Vraag: De kans dat een bepaalde student wordt toegelaten tot een bepaalde universiteit is 0,2. Als er 10 studenten zich aanmelden, wat is dan de kans dat er meer dan 4 worden geaccepteerd?

Antwoord: Met behulp van de binomiale verdelingscalculator hierboven met p = 0,2, n = 10 en k = 4, vinden we dat P(X>4) = 0,03279 .

Probleem 4

Vraag: Je gooit een munt 12 keer op. Wat is het verwachte gemiddelde aantal koppen dat zal verschijnen?

Antwoord: Bedenk dat het gemiddelde van een binominale verdeling wordt berekend als μ = np. Dus μ = 12*0,5 = 6 koppen .

Probleem 5

Vraag: Mark slaat een homerun op 10% van zijn pogingen. Als hij in een bepaald spel vijf pogingen doet, wat is dan de variantie in het aantal homeruns dat hij slaat?

Antwoord: Bedenk dat de variantie van een binominale verdeling wordt berekend als σ ² = np(1-p). Dus ^σ2 = 6*.1*(1-.1) = 0,54 .

Aanvullende bronnen

De volgende artikelen kunnen u helpen bij het leren gebruiken van de binominale verdeling in verschillende statistische software:

• Hoe binomiale kansen in Excel te berekenen
• Hoe binomiale kansen te berekenen op een TI-84-rekenmachine
• Hoe binomiale kansen in R te berekenen
• Hoe een binominale verdeling in R te plotten