Percentielen (statistieken)
In dit artikel wordt uitgelegd wat een percentiel is en hoe het wordt berekend. U vindt opgeloste percentieloefeningen en bovendien kunt u elk percentiel van uw gegevensmonster berekenen met een online rekenmachine.
Wat zijn percentielen?
In de statistieken zijn percentielen de waarden die een reeks geordende gegevens in honderd gelijke delen verdelen. Een percentiel geeft dus de waarde aan waaronder een percentage van de dataset valt.
De waarde van het 35e percentiel is bijvoorbeeld hoger dan 35% van de waargenomen gegevens, maar lager dan de rest van de gegevens.
Percentielen worden weergegeven door de hoofdletter P en de percentielindex, dat wil zeggen: het 1e percentiel is P 1 , het 40e percentiel is P 40 , het 79e percentiel is P 79 , enzovoort.

👉 U kunt de onderstaande rekenmachine gebruiken om percentielen van elke dataset te berekenen.
Op dezelfde manier zijn percentielen een maatstaf voor de niet-centrale positie, samen met kwartielen, kwintielen en decielen. U kunt de betekenis van elk van deze kwantieltypen op onze website controleren.
Opgemerkt moet worden dat de term percentielen ook wordt gebruikt om het gewicht en de lengte van een baby te vergelijken met de standaardwaarden van andere baby’s, omdat er groeitabellen zijn met geregistreerde waarden die helpen bepalen of de baby correct groeit of niet. . .
Hoe percentielen te berekenen
Om de positie van een percentiel van een statistische gegevensreeks te berekenen , moet u het percentielgetal vermenigvuldigen met de som van het totale aantal gegevenspunten plus één en het resultaat delen door honderd.
De percentielformule is daarom:
![]()
Let op: deze formule vertelt ons de positie van het percentiel, maar niet de waarde ervan. Het percentiel bestaat uit de gegevens die zich bevinden op de positie die door de formule wordt verkregen.
Soms geeft het resultaat van deze formule ons echter een decimaal getal. We moeten daarom twee gevallen onderscheiden, afhankelijk van of het resultaat een decimaal getal is of niet:
- Als het resultaat van de formule een getal zonder decimaal deel is, komt het percentiel overeen met de gegevens die zich in de positie bevinden die door de bovenstaande formule wordt verstrekt.
- Als het resultaat van de formule een getal met een decimaal deel is, wordt de exacte percentielwaarde berekend met behulp van de volgende formule:
![]()
Waar x i en x i+1 de getallen zijn van de posities waartussen het getal verkregen door de eerste formule zich bevindt, en d het decimale deel is van het getal verkregen door de eerste formule.
Je denkt nu misschien dat het vinden van de percentielen van een statistische steekproef of populatie ingewikkeld is omdat de methode uit veel stappen bestaat, maar in werkelijkheid is het eenvoudig. Lees de volgende twee concrete voorbeelden en ik weet zeker dat je het veel beter zult begrijpen.
Opmerking : de wetenschappelijke gemeenschap is het nog niet volledig eens over de manier waarop percentielen moeten worden berekend, dus u kunt een statistiekboek vinden waarin dit iets anders wordt uitgelegd.
Voorbeelden van percentielberekeningen
Zoals je hierboven hebt gezien bij de uitleg over het vinden van de percentielen van een steekproef, varieert de berekening afhankelijk van het feit of het resultaat van de eerste formule decimaal is of niet. Daarom vindt u hieronder twee opgeloste voorbeelden, één voor elk geval.
voorbeeld 1
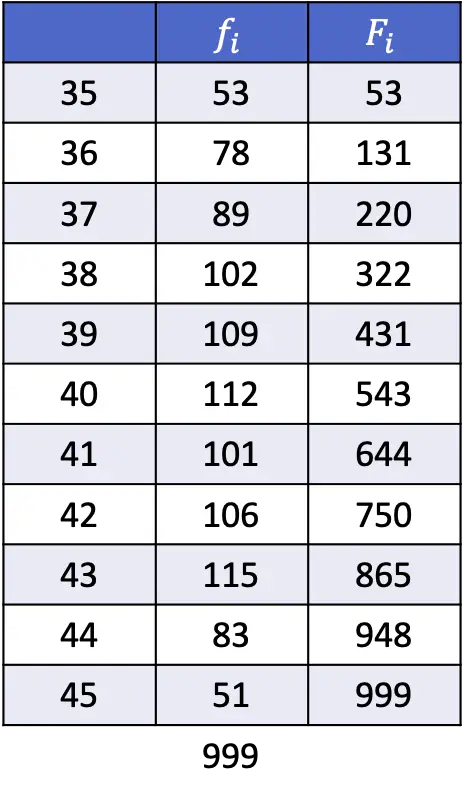
- Bereken uit de gegevens in de volgende tabel het 1e, 43e en 89e percentiel.
Zoals uitgelegd in de vorige sectie, is de formule voor het vinden van de positie van een percentiel:
![]()
In dit geval is de steekproefomvang voor deze oefening 999 statistische gegevens, dus om de positie van het eerste percentiel te berekenen moeten we 999 vervangen door n en 1 door k :
![]()
Het 1e percentiel zal dus degene zijn waarvan de cumulatieve absolute frequentie onmiddellijk groter is dan 10, wat in dit geval 35 is omdat het een cumulatieve absolute frequentie van 53 heeft.
Om het 43e percentiel te bepalen moet je dezelfde formule gebruiken, maar deze keer vervangen we uiteraard de k door 43.
![]()
De absolute cumulatieve frequentie direct boven 430 is 431 van gegevens 39, dus het 43e percentiel is gelijk aan 39.
Ten slotte passen we dezelfde formule toe om het 89e percentiel te verkrijgen:
![]()
De cumulatieve absolute frequentie van de waarde 44 is 948, wat onmiddellijk groter is dan 890. Daarom is het 89e percentiel 44.
Voorbeeld 2
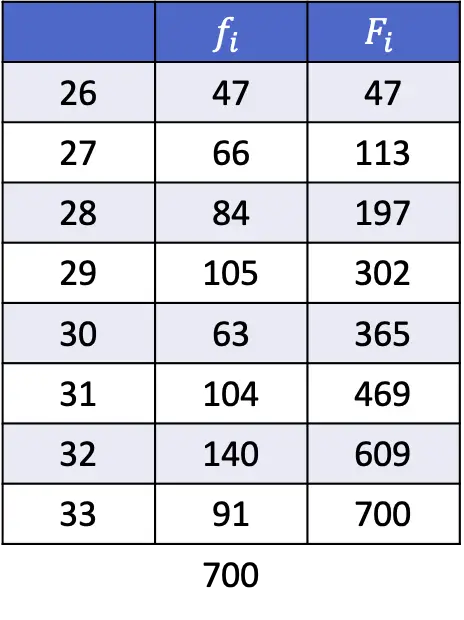
- Zoek het 35e en 67e percentiel van de volgende gegevensreeksen:
Zelfs als we in deze oefening meer berekeningen zullen moeten doen, is het principe nog steeds hetzelfde: we moeten de percentielpositie berekenen met de volgende uitdrukking.
![]()
Om het 35e percentiel te berekenen vervangen we dus de k door 35 en de n door het totale aantal gegevens, dat wil zeggen 700:
![]()
Maar deze keer hebben we een decimaal getal uit de formule gehaald, dus moeten we de volgende algebraïsche uitdrukking toepassen om de exacte percentielwaarde te berekenen:
![]()
Het getal gegeven door de eerste formule is 245,35, dus het 35e percentiel ligt tussen posities 245 en 246, wat overeenkomt met respectievelijk de waarden 29 en 29. Daarom is x i gelijk aan 29, x i+1 is 29 en d is het decimale deel van het verkregen getal waard, dat wil zeggen 0,35.
![]()
Om het 67e percentiel te vinden, moeten we dezelfde methode gebruiken. We berekenen eerst de percentielpositie:
![]()
Het resulterende getal 469,67 geeft aan dat het percentiel tussen de posities 469 en 470 zal liggen, waarvan de waarden 31 en 32 zijn. Daarom gebruiken we de tweede formule in het proces om de exacte percentielwaarde te vinden:
![]()
percentiel rekenmachine
Voer een statistische gegevensset en het percentielnummer dat u wilt berekenen in de volgende rekenmachine in. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.
Percentielen in gegroepeerde gegevens
Om percentielen te berekenen wanneer gegevens in groepen worden gegroepeerd , moeten we eerst de groep of klasse vinden waarin het percentiel valt met behulp van de volgende formule:
![]()
Het percentiel zal daarom in het interval liggen waarvan de absolute frequentie onmiddellijk groter is dan het getal verkregen in de vorige uitdrukking.
En zodra we al weten tot welk interval het percentiel behoort, moeten we de volgende formule toepassen om de exacte waarde van het percentiel te vinden:
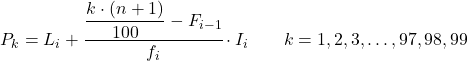
Goud:
- Li is de ondergrens van het interval waarin het percentiel ligt.
- n is het totale aantal waarnemingen.
- Fi -1 is de cumulatieve absolute frequentie van het vorige interval.
- fi is de absolute frequentie van het interval waarin het percentiel ligt.
- I i is de breedte van het percentielinterval.
Hieronder vindt u een stapsgewijze oefening over hoe u percentielen kunt verkrijgen wanneer gegevens in intervallen worden uitgedrukt. Concreet worden de 29e, 52e en 98e percentielen berekend.

De gegevens in dit voorbeeld zijn gegroepeerd als intervallen, dus we moeten twee stappen uitvoeren om de percentielen te bepalen: eerst moeten we het interval vinden waarin het percentiel valt en vervolgens de formule toepassen om de exacte waarde van het percentiel te berekenen. percentiel.
We vinden dus de positie van het 29e percentiel met de volgende uitdrukking:
![]()
![]()
Het percentielinterval is het interval waarvan de cumulatieve absolute frequentie onmiddellijk groter is dan 145,29, wat in dit geval het interval [350,375) is waarvan de cumulatieve absolute frequentie 175 is. En zodra we het percentielinterval kennen, passen we de volgende formule toe om het interval te berekenen. exacte waarde:
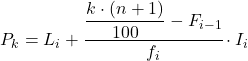
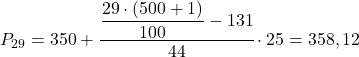
Nu herhalen we dezelfde procedure om het 52e percentiel te berekenen. We berekenen eerst het interval:
![]()
Het 52e percentielinterval is [400,425), aangezien de cumulatieve absolute frequentie (298) direct boven 260,52 ligt. De exacte waarde van het percentiel zal daarom zijn:
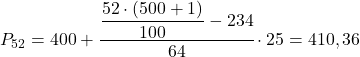
Ten slotte vinden we het 98e percentiel. Zoals altijd berekenen we eerst het interval waar het ligt:
![]()
En zodra we het interval kennen waar het percentiel ligt, berekenen we de exacte waarde ervan met de volgende formule: