Een inleiding tot multinomiale distributie

De multinomiale verdeling beschrijft de waarschijnlijkheid van het verkrijgen van een specifiek aantal tellingen voor k verschillende uitkomsten, wanneer elke uitkomst een vaste waarschijnlijkheid van voorkomen heeft.

_{Als een} willekeurige variabele _{_} kan worden gevonden met de volgende formule:

Waarschijnlijkheid = n! * (p ₁ ^{x ₁} * p ₂ ^{x ₂} * … * p _k ^{x _k} ) / (x ₁ ! * x ₂ ! … * x _k !)

Goud:

• n: totaal aantal evenementen
• x ₁ : aantal keren dat resultaat 1 voorkomt
• p ₁ : waarschijnlijkheid dat resultaat 1 optreedt in een bepaalde poging

Stel bijvoorbeeld dat er 5 rode knikkers, 3 groene knikkers en 2 blauwe knikkers in een urn zitten. Als we willekeurig 5 knikkers uit de urn trekken, met vervanging, wat is dan de kans dat we precies 2 rode knikkers, 2 groene knikkers en 1 blauwe knikker krijgen?

Om deze vraag te beantwoorden, kunnen we de multinomiale verdeling gebruiken met de volgende parameters:

• n : 5
• x ₁ (# rode knikkers) = 2, x ₂ (# groene knikkers) = 2, x ₃ (# blauwe knikkers) = 1
• p ₁ (rood waarschijnlijk) = 0,5, p ₂ (groen waarschijnlijk) = 0,3, p ₃ (blauw waarschijnlijk) = 0,2

Als we deze getallen in de formule stoppen, ontdekken we dat de waarschijnlijkheid:

Waarschijnlijkheid = 5! * (.5 ² * .3 ² * .2 ¹ ) / (2! * 2! * 1!) = 0,135 .

Praktijkproblemen met multinomiale distributie

Gebruik de volgende oefenproblemen om uw kennis van de multinomiale verdeling te testen.

Opmerking: we zullen de Multinomiale Verdelingscalculator gebruiken om de antwoorden op deze vragen te berekenen.

Probleem 1

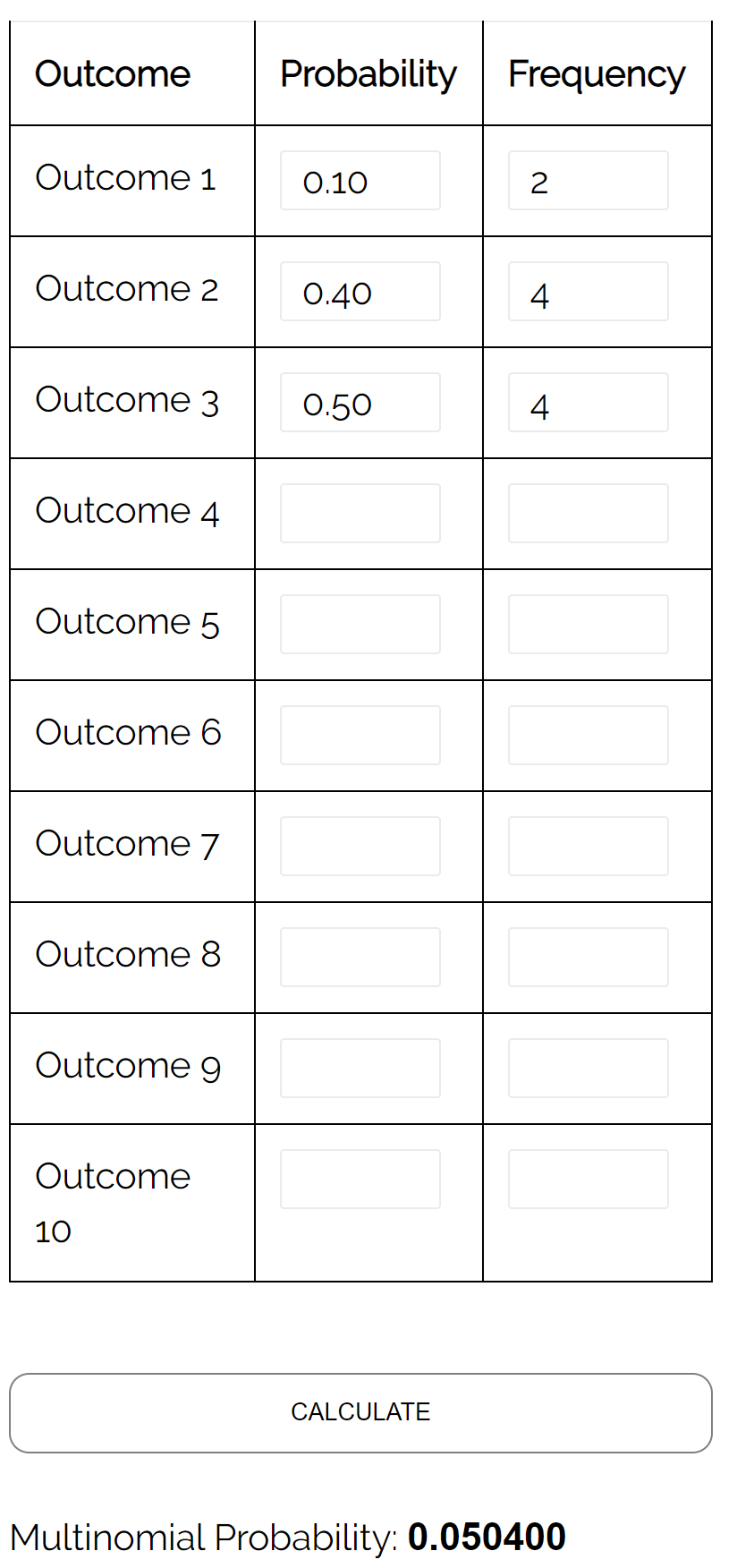
Vraag: Bij een drievoudige verkiezing voor burgemeester krijgt kandidaat A 10% van de stemmen, kandidaat B 40% van de stemmen en kandidaat C 50% van de stemmen. Als we een willekeurige steekproef van 10 kiezers selecteren, wat is dan de kans dat 2 op kandidaat A hebben gestemd, 4 op kandidaat B hebben gestemd en 4 op kandidaat C hebben gestemd?

Antwoord: Met behulp van de Multinomiale Verdelingscalculator met de volgende invoer vinden we dat de waarschijnlijkheid 0,0504 is:

Probleem 2

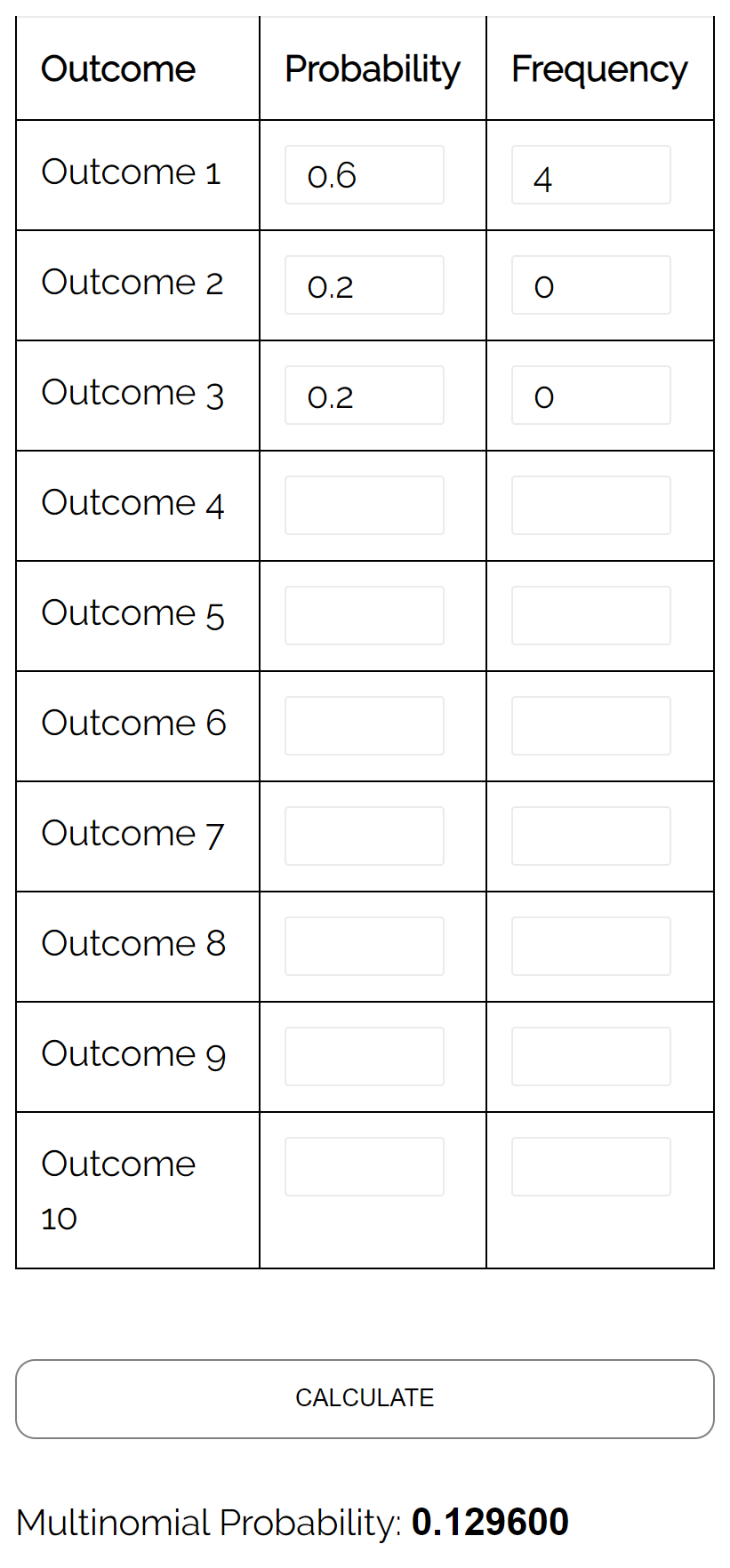
Vraag: Stel dat er in een urn 6 gele knikkers, 2 rode knikkers en 2 roze knikkers zitten. Als we willekeurig 4 ballen uit de urn selecteren, met vervanging, wat is dan de kans dat alle 4 de ballen geel zijn?

Antwoord: Als we de Multinomiale Verdelingscalculator met de volgende invoer gebruiken, ontdekken we dat de waarschijnlijkheid 0,1296 is:

Probleem 3

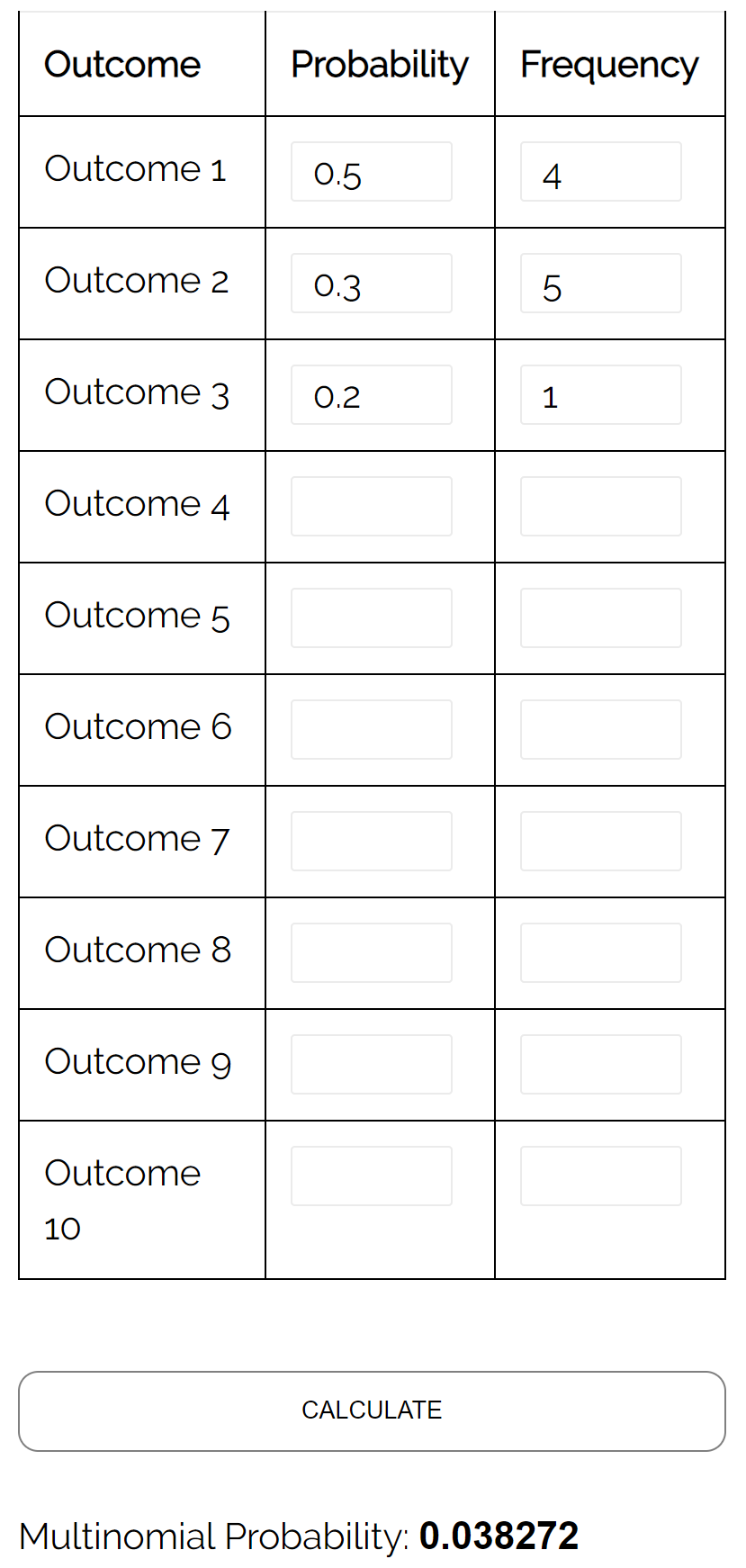
Vraag: Stel dat twee leerlingen tegen elkaar schaken. De kans dat leerling A een bepaald spel wint is 0,5, de kans dat leerling B een bepaald spel wint is 0,3 en de kans dat er een gelijkspel is in een bepaald spel is 0,2. Als hij 10 spellen speelt, wat is dan de kans dat leerling A een bepaald spel wint? kans dat speler A 4 keer wint, speler B 5 keer wint, en dat ze 1 keer gelijk spelen?

Antwoord: Met behulp van de Multinomiale Verdelingscalculator met de volgende invoer vinden we dat de waarschijnlijkheid 0,038272 is:

Aanvullende bronnen

De volgende tutorials bieden een inleiding tot andere veelgebruikte verdelingen in de statistiek:

Een inleiding tot de normale verdeling
Een inleiding tot de binominale verdeling
Een inleiding tot de Poisson-verdeling
Een inleiding tot geometrische distributie